PYTHON - KRUSKAL'S ALGORITHM MINIMUM SPANNING TREE CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

class Node:
	pass
	
class Edge:
	pass
		
map = {}
vertices = []
edgeList = []

def insertVertex(vertex):
	vertices.append(vertex)

def insertEdge(vertex1, vertex2, edgeVal):
	edge = Edge()
	edge.startVertex = vertex1
	edge.endVertex = vertex2
	edge.value = edgeVal
	edgeList.append(edge)

#Create groups with only one vertex.
def createSet(data):
	node = Node()
	node.data = data
	node.rank = 0
	node.parent = node
	map[data] = node

#Combines two groups into one. Does union by rank.
def union(vertex1, vertex2):
	node1 = map[vertex1]
	node2 = map[vertex2]

	parent1 = findSetNode(node1)
	parent2 = findSetNode(node2)

	#If they are in the same group, do nothing.
	if(parent1.data == parent2.data):
		return

	#Else whose rank is higher becomes parent of other.
	if (parent1.rank <= parent2.rank):
		#Increment rank only if both sets have same rank.
		parent1.rank = parent1.rank + 1 if parent1.rank == parent2.rank else parent1.rank
		parent2.parent = parent1
	else:
		parent1.parent = parent2

# Find the representative of this set
def findSet(data):
	return findSetNode(map[data]).data

# Finds the leader/representative recursivly and does PATH COMPRESSION as well.
def findSetNode(node):
	parent = node.parent
	if (parent == node):
		return parent
	node.parent = findSetNode(node.parent)
	return node.parent

# Find Minimum Spanning Tree using Kruskal's Algorithm.
def createMST():
	#Sort all edges in Ascending order.	
	edgeList.sort(key=lambda x: x.value)
	
	#Create as many groups as the total vertices.
	for vertex in vertices:
		createSet(vertex)

	resultEdge = []

	for edge in edgeList:
		#Get the sets of two vertices of the edge.
		root1 = findSet(edge.startVertex)
		root2 = findSet(edge.endVertex)

		#check if the vertices are on the same or different set.
		#If vertices are in the same set then ignore the edge.
		if (root1 == root2):
			continue
		else:
			# If vertices are in different sets then add the edge to result and union 
			# these two sets into one.
			resultEdge.append(edge)
			union(edge.startVertex, edge.endVertex)
	return resultEdge


#Adding vertices one by one

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")

#Adding edges with values.

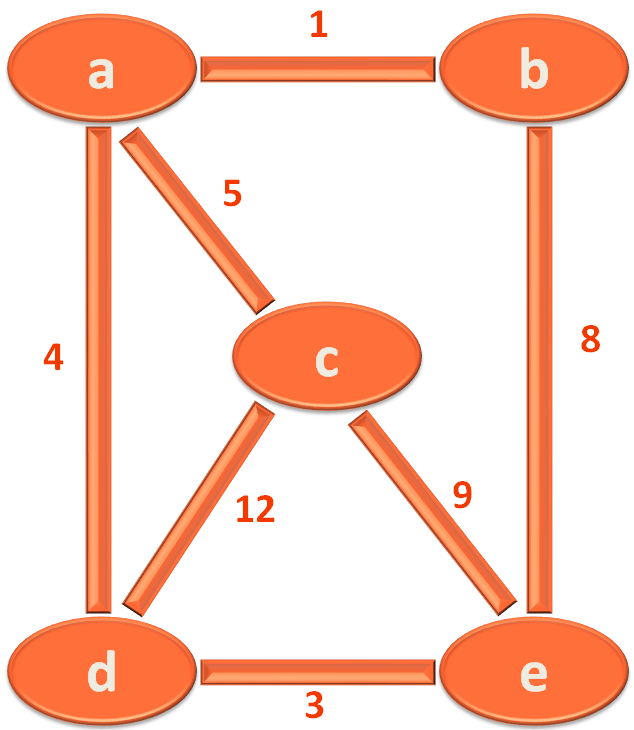
insertEdge("a", "b", 1)
insertEdge("b", "e", 8)
insertEdge("e", "d", 3)
insertEdge("d", "a", 4)
insertEdge("a", "c", 5)
insertEdge("c", "e", 9)
insertEdge("c", "d", 12)

mstList = createMST()

for edge in mstList:
	print("The edge : ",edge.startVertex," -- ",edge.endVertex," with value : ",edge.value)

Output :

The edge : a -- b with value : 1
The edge : e -- d with value : 3
The edge : d -- a with value : 4
The edge : a -- c with value : 5

Brief recap of Kruskal's Algorithm for Minimum Spanning Tree

Note : We have used 'Union by Rank' and 'Path Compression' technique. You can have a look at it. If not, not worries. We will explain in brief.

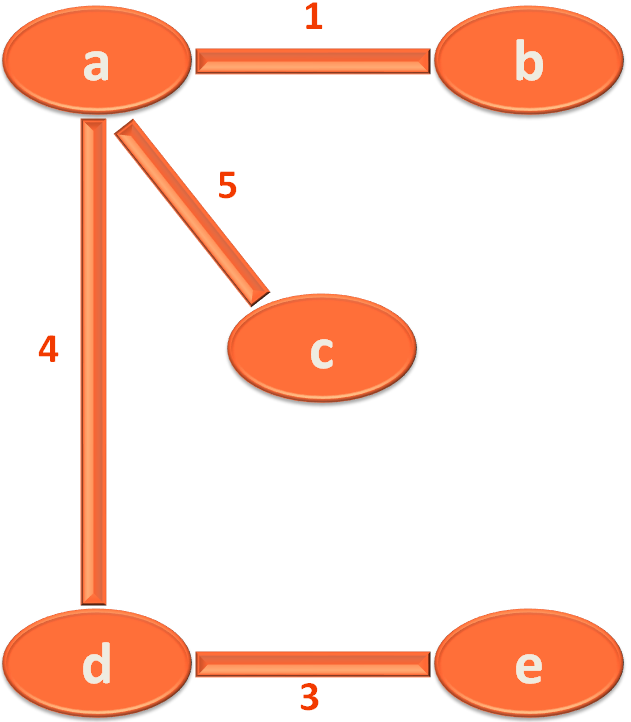
So, we will be dealing with the below Graph,

First thing we do is, sort all the edges in ascending order.

Then, create individual groups for each vertices and initialise with rank 0.
```
1st Group - {a}  --- rank 0
2nd Group - {b}  --- rank 0
3rd Group - {c}  --- rank 0
4th Group - {d}  --- rank 0
5th Group - {e}  --- rank 0
```
Now, we need to elect a leader for each group. And, since there is only one vertex in each group, the individual group member will be marked as leader of their group.

Say for example ,

a is the leader of group 1, b is leader of group 2 and so on.

And leaders are given a superior rank 0.

Next, take the sorted edges, one by one, connect them and increment the leader rank by 1.

For Example :

The first sorted edge is a,b. So, we connect a and b,
```
a --- b
```
Then take a from group 1 and b from group 2.
```
1st Group - {a}  --- rank 0
2nd Group - {b}  --- rank 0
```
And, combine a and b in group 1.
```
1st Group - {a,b}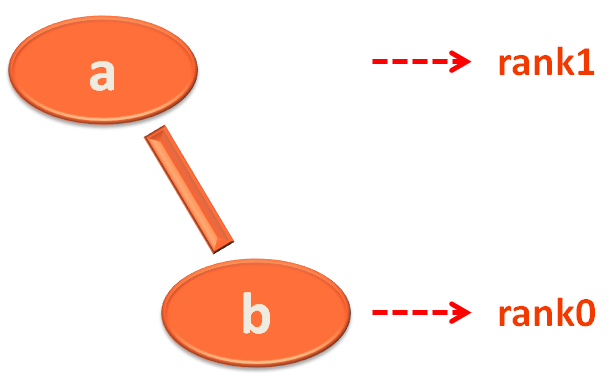
```
Now, it is time to elect a leader for 1st Group.

And a was the leader/representative of group 1 and now, b came to group 1.

So, we make b the child of a. And since a is the leader, a is given rank 1.

And the same steps are repeated.

This feature of combining two groups and ranking them is Union by Rank.

Explanation of the Node class in the above code

In the above code, we have a class called Node. Which looks a little different.

class Node:
	pass

Although it has nothing inside it. But in reality there are three attributes in the Node class. i.e. data, rank and parent.

data of string type
rank of int type
parent of Node type

You can think of the Node class as a representation of a Vertex.

And how is that so ?

Just think, a vertex should have a rank and its name. And so we have,

data of string type
rank of int type

But the only mystery is, what is parent of Node type?

A Node object inside a Node class! Looks Strange! Right?

It is like a connection, we are trying to establish between Vertices.

So, when the vertices are created for the first time, they should the leader of their group and off course they should be their parent.

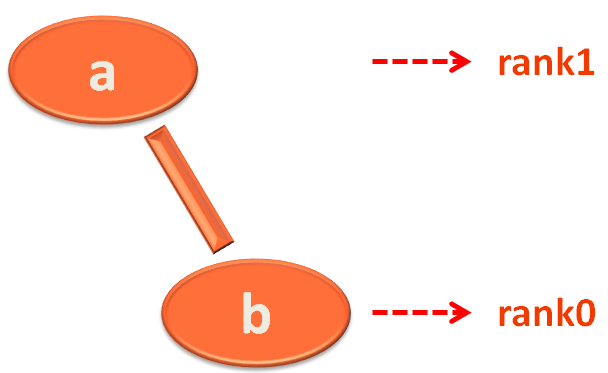
Say for example when vertex a and b is created, a is in group 1 and b is in group 2.

Node parent for vertex b is Node b (Since vertex b is the leader of group 2).

And Node parent for vertex a is Node a (Since vertex a is the leader of group 1).

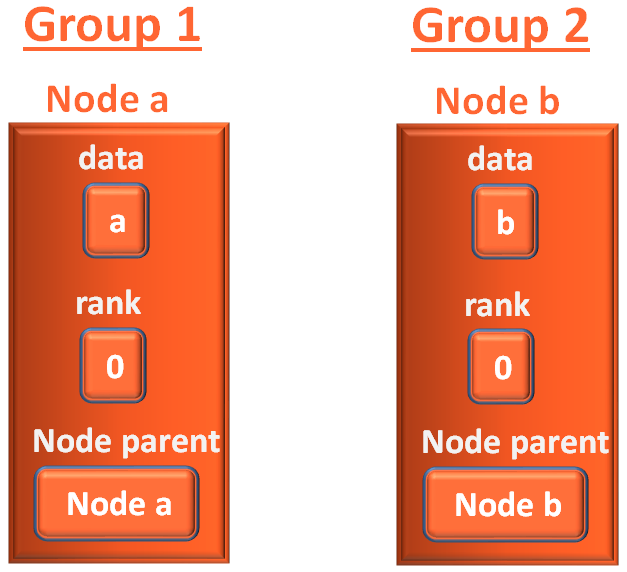
Next, when b is put into group 1, the leader of group 1 is a.

So, vertex b is a child of a.

And Node parent of b is Node a now.

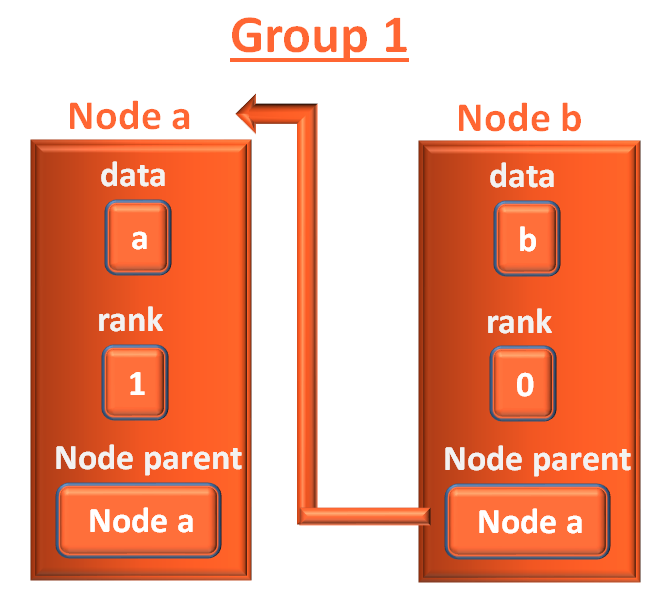
The vertex a is named as Node a and vetex b is named as Node b. We have seen how the connection is established.

Explanation of the Edge class in the above code

As we have seen the Node class is used to store the contents of the Vertices.

Similarly, the Edge class is used to store the contents of the Edges.

class Edge:
	pass

Similarly, the Edge class has three attributes(Well! Once again that is not defined in Edge class),

startVertex

endVertex

value

The above one is the example of an edge that has,

startVertex = a
endVertex = b
value = 1

Code explanation of Kruskal's Algorithm for Minimum Spanning Tree

So, firstly we construct the graph by adding the vertices.

#Adding vertices one by one

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")

Then adding the edges with its values,

#Adding edges with values.

insertEdge("a", "b", 1)
insertEdge("b", "e", 8)
insertEdge("e", "d", 3)
insertEdge("d", "a", 4)
insertEdge("a", "c", 5)
insertEdge("c", "e", 9)
insertEdge("c", "d", 12)

Then we call the createMST() method to construct Minimum Spanning Tree using Kruskal's Algorithm.

mstList = createMST()

Explanation of 'def createMST()' method

def createMST():
	#Sort all edges in Ascending order.
	edgeList.sort(key=lambda x: x.value)

	#Create as many groups as the total vertices.
	for vertex in vertices:
		createSet(vertex)

	resultEdge = []

	for edge in edgeList:
		#Get the sets of two vertices of the edge.
		root1 = findSet(edge.startVertex)
		root2 = findSet(edge.endVertex)

		#check if the vertices are on the same or different set.
		#If vertices are in the same set then ignore the edge.
		if (root1 == root2):
			continue
		else:
			# If vertices are in different sets then add the edge to result and union
			# these two sets into one.
			resultEdge.append(edge)
			union(edge.startVertex, edge.endVertex)
	return resultEdge

As we know, the first task is to sort the Edges based on its value,

edgeList.sort(key=lambda x: x.value)

The next task would be, to create individual groups for each Vertex using the createSet() method.

#Create as many groups as the total vertices.
for vertex in vertices:
	createSet(vertex)

And as we know vertices

vertices = []

contains the List of Vertices. So, we take the vertices one by one using the for each loop and call the creteSet() method.

createSet(vertex)

Explanation of 'def createSet(data)' method

node = Node()
node.data = data
node.rank = 0
node.parent = node
map[data] = node

The parameter data contains the vertex(Say a for vertex a).

So, we create a Node object to hold the actual vertex(Say value a for vertex a)

node.data = data

the rank of the vertex.

node.rank = 0

rank is initialised to 0 because initially all the vertices would be the leader of their group and the leader is ranked 0.

The next line is extremely important,

node.parent = node

Now since, vertex a is the leader of their group. node.parent is vertex a itself.

Below is the example of vertex a.

Then we put the created node in the Dictionary named map,

map = {}

With the key as the value of vertex(a in this case) and value as the created node.

map[data] = node

All the Nodes/vertices are created in the same way and put in the map.

Let us come back to the createMST() method again,

And since we got all the groups created.

Now, it's time for us to implement the actual logic.

And we have declared resultEdge List that will store all the edges included in the Minimum Spanning Tree.

resultEdge = []

Now, we know that the List edgeList,

edgeList = []

Contains the List of all the edges in the Graph(Off course Sorted in ascending order done earlier).

And what will will do is take List edgeList one by one and try constructing the Minimum Spanning Tree.

for edge in edgeList:
	#Get the sets of two vertices of the edge.
	root1 = findSet(edge.startVertex)
	root2 = findSet(edge.endVertex)

	#check if the vertices are on the same or different set.
	#If vertices are in the same set then ignore the edge.
	if (root1 == root2):
		continue
	else:
		# If vertices are in different sets then add the edge to result and union
		# these two sets into one.
		resultEdge.append(edge)
		union(edge.startVertex, edge.endVertex)

So, the for each loop, takes the sorted edges one by one,

for edge in edgeList

And the first thing it does is, tries to find the leader of each vertex using the findSet() method,

root1 = findSet(edge.startVertex)
root2 = findSet(edge.endVertex)

Explanation of 'def findSet(data)' method

def findSet(data):
	return findSetNode(map[data]).data

Now, the cool thing to note is, the return statement,

return findSetNode(map[data]).data

Calls another findSetNode(...) method.

Sounds Interesting or Strange ?

Let's dive in,

map[data] from the return statement,

return findSetNode(map[data]).data

gives us a Node object.

How ?

Because, we have seen map holds Key as the Vertex name (Say a) and its Node as value.

And if we pass the value a to the Dictionary,

map["a"]

We get the Node object of a.

So, this time we will be calling the findSetNode(...) method, that accepts Node as parameter.

And luckily, we have the def findSetNode(node) method.

Explanation of 'def findSetNode(node)' method

parent = node.parent
if (parent == node):
	return parent
node.parent = findSetNode(node.parent)
return node.parent

So, in the first line, we have created a Node variable called parent and initialised the parent variable with the parent from the parameter node of Node type.

Say, we have passed Node a and the parent of Node a is Node a(Because Node a is the leader).

parent = node.parent

Then we check if the Node parent is equal to the node from parameter Node node.

if (parent == node):
	return parent

In this case Node parent and Node node are equal.

So, the Node parent is returned.

But ! Yes there is a BUT.

Say, the node b was passed, when it was a child of a.

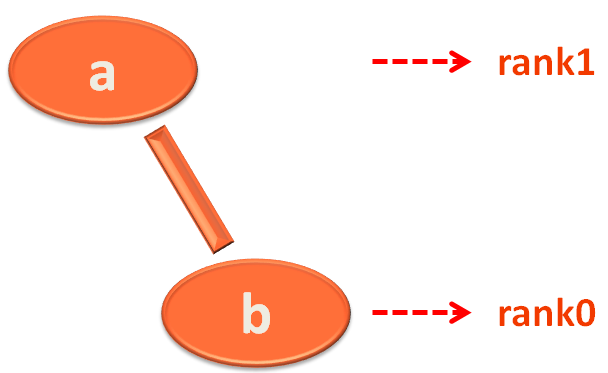
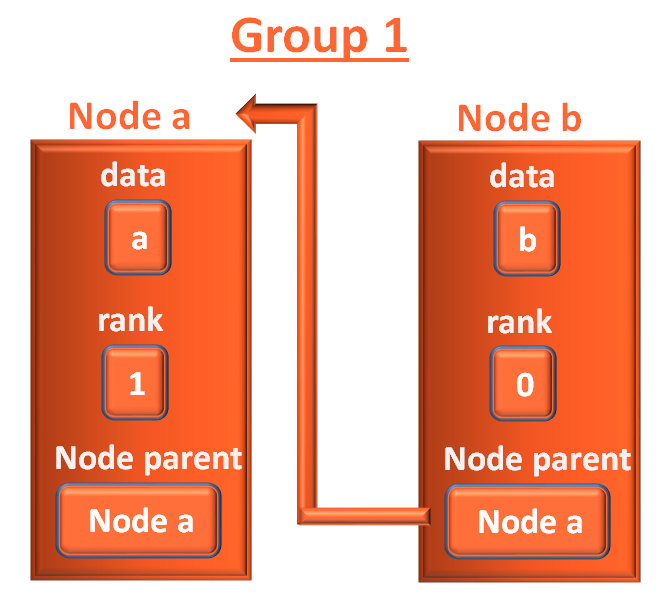
Now, let us relook the steps for Node b,

parent = node.parent

So, Node parent would be Node a.

And Node parent would be holding the Node a.

Then we check if the Node parent is equal to the node from parameter Node node.

if (parent == node):
	return parent

And if condition is not satisfied as

Node parent is holding Node a and node is holding Node b.

Fair enough !

Then we go to the next line, where findSet(Node node) method is called recursively,

node.parent = findSetNode(node.parent)

Until it finds the parent and finally node.parent is returned.

return node.parent

So, let us come back to createMST() method again.

Let us take the example of edge

root1 = findSet(edge.startVertex)
root2 = findSet(edge.endVertex)

Where, edge.startVertex is a and edge.endVertex is b.

And we found the parent of a is a itself and parent of b is b.

So ,

root1 = "a"

and

root2 = "b"

And, if we see the code again,

for edge in edgeList:
	#Get the sets of two vertices of the edge.
	root1 = findSet(edge.startVertex)
	root2 = findSet(edge.endVertex)

	#check if the vertices are on the same or different set.
	#If vertices are in the same set then ignore the edge.
	if (root1 == root2):
		continue
	else:
		# If vertices are in different sets then add the edge to result and union
		# these two sets into one.
		resultEdge.append(edge)
		union(edge.startVertex, edge.endVertex)

There is this if statement that checks,

if (root1 == root2)

But in this case root1 is a and root2 is b.

So, we come to the else part.

else:
		# If vertices are in different sets then add the edge to result and union
		# these two sets into one.
		resultEdge.append(edge)
		union(edge.startVertex, edge.endVertex)

Now since, we are in the else part. This edge,

must be included in the Minimum Spanning Tree.

resultEdge.append(edge)

And thus, we have added it to the resultEdge list.

So, the next task would be to combine a and b in the same group.

union(edge.startVertex, edge.endVertex)

And this task of combining is done by the union(...) method.

Explanation of 'def union(vertex1, vertex2)' method

node1 = map[vertex1]
node2 = map[vertex2]

parent1 = findSetNode(node1)
parent2 = findSetNode(node2)

#If they are in the same group, do nothing.
if(parent1.data == parent2.data):
	return

#Else whose rank is higher becomes parent of other.
if (parent1.rank <= parent2.rank):
	#Increment rank only if both sets have same rank.
	parent1.rank = parent1.rank + 1 if parent1.rank == parent2.rank else parent1.rank
	parent2.parent = parent1
else:
	parent1.parent = parent2

Let us take the example of

to explain the union(...) method.

node1 = map[vertex1]
node2 = map[vertex2]

And

node2 will have the contents of Node b and node1 will have the contents of Node a.

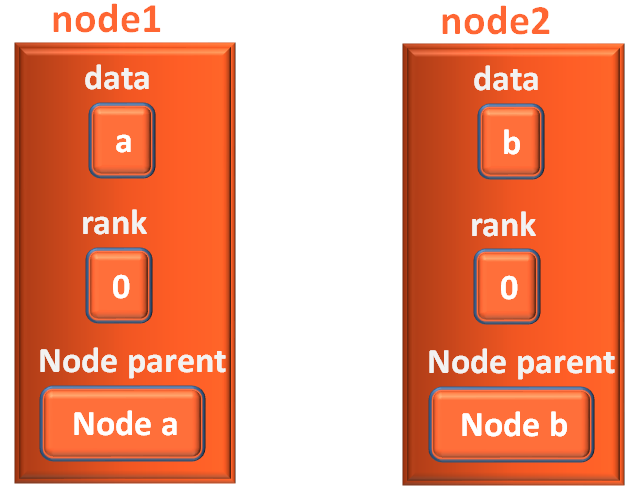
In the next two lines,

parent1 = findSetNode(node1)
parent2 = findSetNode(node2)

We try to find the parents/leaders of node1 and node2 using findSet(node) method which we have already seen.

And in this case, the parent of a is a and the parent of b is b.

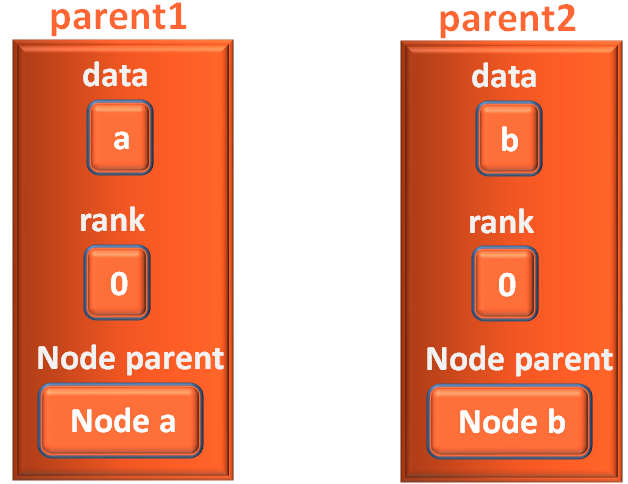
Next, we check, if both the parent of the vertices are equal or not,

if(parent1.data == parent2.data):
	return

If both the parents are equal, we do nothing.

But in this case, they are not equal as

parent1.data = "a"

and

parent2.data = "b"

So, we come to the next if statement.

if (parent1.rank <= parent2.rank):
	#Increment rank only if both sets have same rank.
	parent1.rank = parent1.rank + 1 if parent1.rank == parent2.rank else parent1.rank
	parent2.parent = parent1
else:
	parent1.parent = parent2

In the if statement, we check if parent1.rank is less than or equal to parent2.rank.

if (parent1.rank <= parent2.rank)

And in this case,

parent1.rank and parent2.rank has the same rank i.e. 0 (From the above diagram).

And in the next line,

parent1.rank = parent1.rank + 1 if parent1.rank == parent2.rank else parent1.rank

We increment the parent1.rank only if parent1.rank is equal to parent2.rank.

And in this case parent1.rank is equal to parent2.rank,

So, we increment parent1.rank by 1.

parent1.rank + 1

And parent1.rank becomes,

parent1.rank = 1

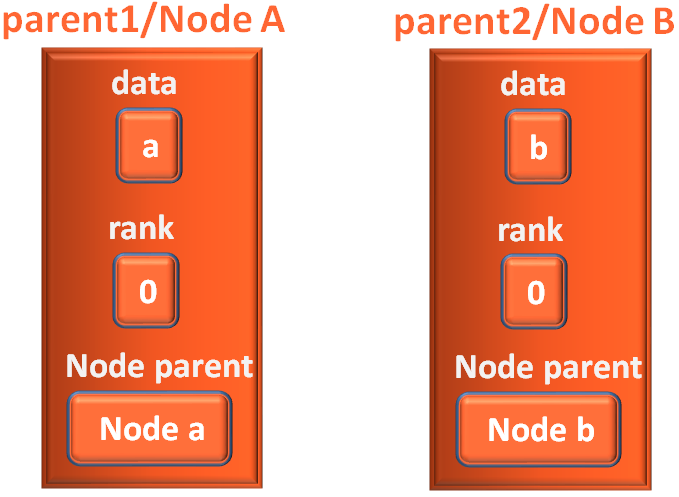
Then, we initialise parent2.parent with parent1.

parent2.parent = parent1

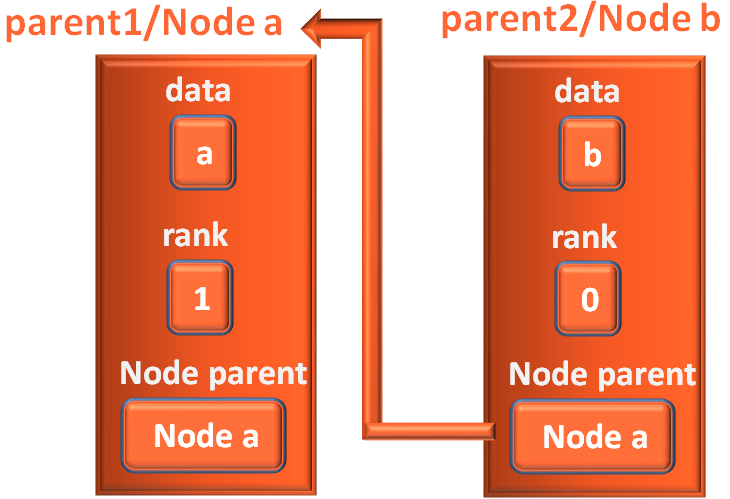
And we can see that the connection between a and b is established,

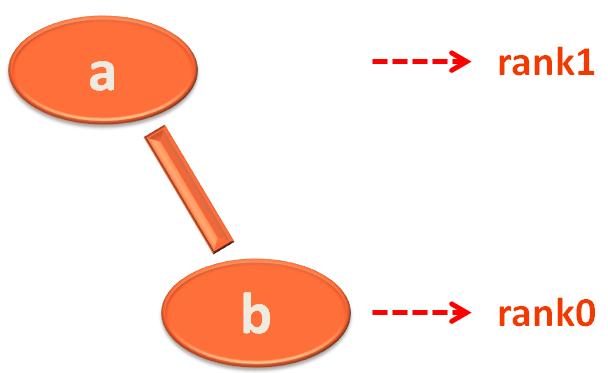
And continuing this way, we get the Minimum Spanning Tree,

❮❮ PREV NEXT ❯❯