HEAP SORT CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

As we know, there is a three step process involved in Heap Sort :

Build a Heap.

Use Heapify.

Remove the Minimum element.

We will be using arrays for implementing Heap and sort the values in descending order.

Example :

public class HeapSort {

    void heapify(int arr[],int root, int length) {

        int left = (2*root)+1;
        int right = (2*root)+2;
        int smallest = root;

        if (left < length && right <= length && arr[right] < arr[left]) {

            smallest = right;
        }
        else if (left <= length){

            smallest = left;
        }

        if (arr[root] > arr[smallest]) {

            int temp = arr[root];
            arr[root] = arr[smallest];
            arr[smallest] = temp;

            heapify(arr, smallest, length);
        }
    }
    
    
    public void buildHeap(int arr[]) {

        int len = arr.length-1;

        for (int parent = (len-1)/ 2; parent >= 0; parent--)
            heapify(arr, parent, len);
    }
    
    public void deleteMin(int arr[]) {

        int len = arr.length-1;

        // Extract elements one by one from Heap
        for (int last=len; last>0; last--) {
            
            int temp = arr[0];
            arr[0] = arr[last];
            arr[last] = temp;

            
            heapify(arr, 0, last-1);
        }
    }

    public void sort(int arr[]) {

        // Build heap (rearrange array)   
        buildHeap(arr);

        deleteMin(arr);
        
    }

    public static void main(String[] args) {
        
        int arr[] = {4,78,32,2,45,11};

        System.out.println("Array before Sorting");

        for (int i=0; i<arr.length; i++)
            System.out.print(arr[i] + " ");

        HeapSort heapSort = new HeapSort();
        
        heapSort.sort(arr);

        System.out.println("Array after Sorting");

        for (int i=0; i<arr.length; i++)
            System.out.print(arr[i] + " ");

    }
}

Code Explanation

So, in the above code we have four methods :

void buildHeap(int arr[ ])

void heapify(int arr[ ],int root, int length)

void deleteMin(int arr[ ])

void sort(int arr[ ])

The best thing about the methods are, they are quite self explanatory.

As we know, the process involved in HeapSort are :

Build a Heap.

Use Heapify.

Remove the Minimum element and place it at the end of the array.

And that's exactly what the above methods are doing.

The 'buildHeap(...)' method is building the Heap. Also, 'buildHeap(...)' method takes the help of 'Heapify(...)' method to construct the Heap.

Then 'deleteMin(...)' method comes into picture, which takes the minimum element from the root and places at the end of the array. Then uses 'Heapify(...)' method to correct the Heap.

And, finally we have the 'sort(...)' method, that clubs all the methods and gives us a sorted result.

Let us understand the entire flow :

Initially, we take the array,

int arr[] = {4,78,32,2,45,11};

And pass it to the 'sort(...)' method,

heapSort.sort(arr);

The 'sort(...)' method is quite simple.

public void sort(int arr[]) {

    // Build heap (rearrange array)   
    buildHeap(arr);

    deleteMin(arr);
        
}

It calls the 'buildHeap(...)' method for building the array.

Then calls the 'deleteMin(...)' method for deleting the minimum element from the the root and place it at the end of the array.

Let us discuss 'void buildHeap(int arr[ ])' method in detail :

public void buildHeap(int arr[]) {

    int len = arr.length-1;

    for (int parent = (len-1)/ 2; parent >= 0; parent--)
        heapify(arr, parent, len);
}

Let us understand the above method with the existing structure.

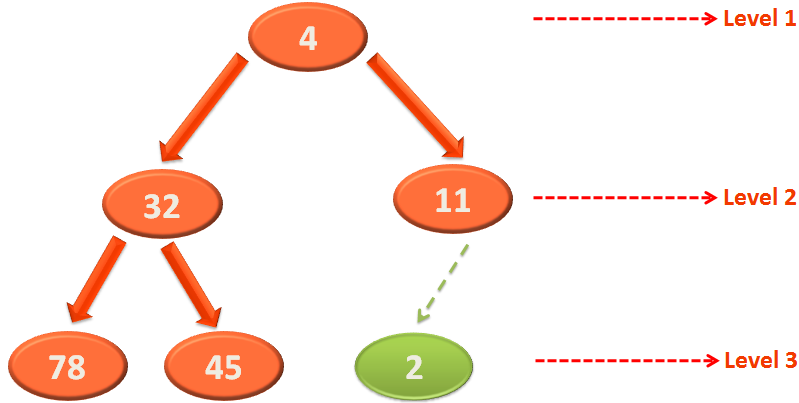
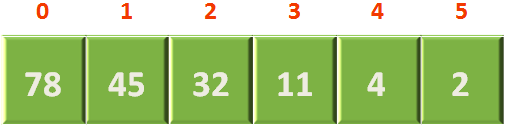
We have an array of 6 numbers,

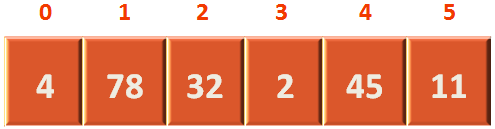
Let us form a logical binary tree with it,

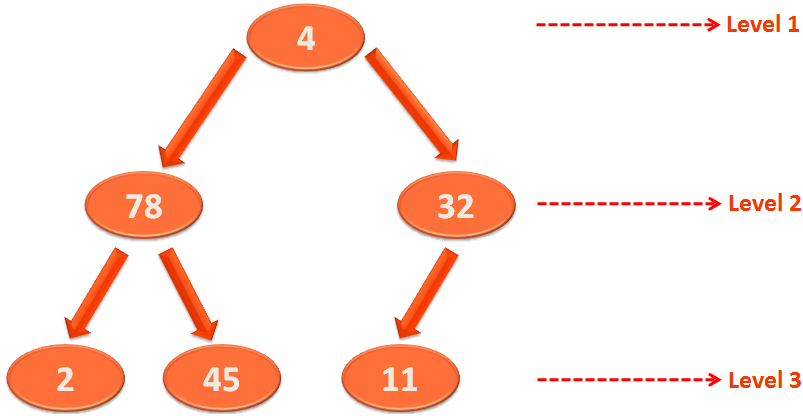
As we know, the elements in Level 3 satisfies the Heap property, as they don't have any child Nodes.

So, we need to target the Nodes of Level 2 and apply 'Heapify' on them.

And that's exactly what we are doing,

for (int parent = (len-1)/ 2; parent >= 0; parent--)
        heapify(arr, parent, len);

We have taken the last element and calculated its parent.

i.e. The formula to calculate the parent is

parent = (element-1)/2

The position of last element is 5.

So, parent = (len-1)/2
    parent = (5-1)/2 = 2

And the parent of arr[5] (i.e. 11) is arr[2] (i.e. 32).

So, the for loop becomes,

for (int parent = 2; parent >= 0; parent--)
        heapify(arr, parent, len);

Now, is it clear?

We are running the 'for' loop, starting with the parents and applying 'Heapify' on each of them.

Say for example, we will apply Heapify on 32 at first,

Then apply Heapify on,

And loop goes on until it reaches the root.

Now, let us discuss 'void heapify(int arr[],int root, int length)' method in detail :

void heapify(int arr[],int root, int length) {

    int left = (2*root)+1;
    int right = (2*root)+2;
    int smallest = root;

    if (left < length && right <= length && arr[right] < arr[left]) {

        smallest = right;
    }
    else if (left <= length){

        smallest = left;
    }

    if (arr[root] > arr[smallest]) {

        int temp = arr[root];
        arr[root] = arr[smallest];
        arr[smallest] = temp;

        heapify(arr, smallest, length);
    }
}

Let us take a small chunk of the Heap and understand the above Heapify code :

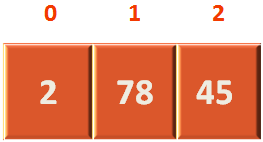
So, the array representation of the above Heap would be,

So the 'root' variable would contain '0' and 'length' variable would contain '2' .

void heapify(int arr[],int root, int length)

Similarly, 'left' variable would be '1'.

int left = (2*root)+1;
As, left = (2*0)+1 = 1

And, 'right' variable would be '2'.

int right = (2*root)+2;

Next, we have initialised the 'smallest' variable with the 'root' variable(We will explain this soon).

int smallest = root;

The 'smallest' variable denotes the position.

Now, let us revisit the logic of Heapify.

- If the right child is less than the left child, right child is smallest. Else left child is the smallest.

That's exactly we have done in the code.

if (left < length && right <= length && arr[right] < arr[left]) {

    smallest = right;
}
else if (left <= length){

    smallest = left;
}

We are checking, if 'arr[right]' is less than 'arr[left]'. If so, we can consider right element is the smallest. And can initialise,

smallest = right;

Else, we can suppose left element is the smallest element and can initialise,

smallest = left;

To simplify,

arr[smallest] = 2 (Since, the left value is smaller than the right)

But what about the condition 'left < length && right <= length' in the 'if' statement and 'left <= length'. Don't worry ! We will explain it soon.

Now, since we have found out the smallest of left and right. According to the logic of Heapify,

- If the root element is greater than the smallest of its right and left element. We need to swap them.

And, so we have done,

if (arr[root] > arr[smallest]) {

    int temp = arr[root];
    arr[root] = arr[smallest];
    arr[smallest] = temp;

    heapify(arr, smallest, length);
}

We have checked if the root element 'arr[root]' (i.e. arr[0] or 78) is greater than arr[smallest] (i.e. arr[1] or 2).

If so, we swap it.

int temp = arr[root];
arr[root] = arr[smallest];
arr[smallest] = temp;

And the new Heap becomes.

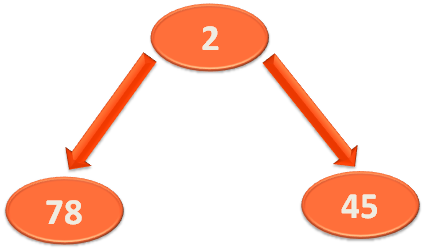
Then we make a recursive call to 'heapify(...)' method, to check if there are any more children or not(In this case we have 3 elements but there can be more elements).

So, in the recursive call to 'heapify(...)' method. We substitute the 'root' variable with the 'smallest' variable.

Note : We will understand this recursive call, once we start explaining the entire flow.

So, the 'heapify(...)' method is called with the new set of values,

void heapify(int arr[],int root, int length) {

Now, root = 1. (Because we have initialised 'smallest' to 'root' in the recursive call).i.e. root is pointing arr[1] where 78 lies.

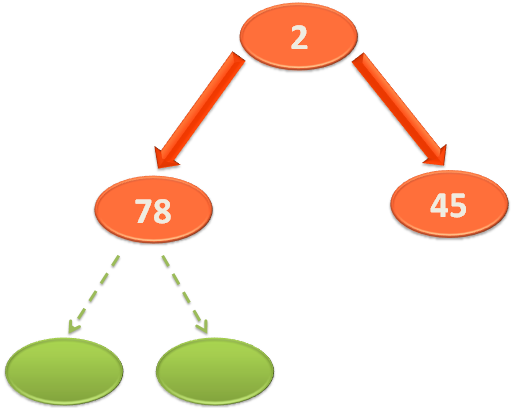
But the strange thing is, 'left' is referring to a location '3'. That does not exist.

int left = (2*root)+1;  
    left = (2*1)+1
    left = 3

At the same time right is referring to location '4'. Which doesn't exist as well.

int right = (2*root)+2;
    right = (2*1)+2
    right = 4

Now, if we refer to arr[3] or arr[4], it will throw an ArrayIndexOutOfBounds exception.

And the below condition comes to rescue at this point.

if (left < length && right <= length && arr[right] < arr[left]) {

    smallest = right;
}
else if (left <= length){

    smallest = left;
}

The condition 'left < length && right <= length' checks, if the left and right element exists or not.

As in this case 'left' and 'right' element doesn't exist.

And the value of 'left' is 3 and 'right' is 4. But the value of 'length' is 2.

So, the condition 'left < length && right <= length' fails.

And it comes to the 'else' statement,

else if (left <= length){

    smallest = left;
}

Even this condition fails, as 'left' is 3 and 'length' is 2.

Now, the question would be, what would be the value of 'smallest'?(As none of the 'if' conditions met).

And, this is the time, the default initialisation of 'smallest' variable comes into picture.

int smallest = root;

And the next 'if' statement containing the recursive call to 'heapify(...)' fails (Since , arr[root] is never greater than arr[root]. As root = smallest).

if (arr[root] > arr[smallest]) {

    int temp = arr[root];
    arr[root] = arr[smallest];
    arr[smallest] = temp;

    heapify(arr, smallest, length);
}

And the method exits as the recursive call to 'heapify(...)' fails.

Let us see the bigger picture combining 'buildHeap(...)' and 'heapify(...)'

So far we have dealt with the numbers 78, 2 and 45.

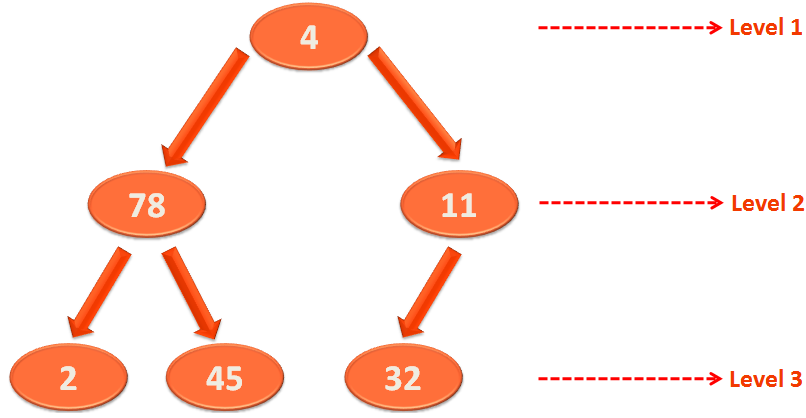
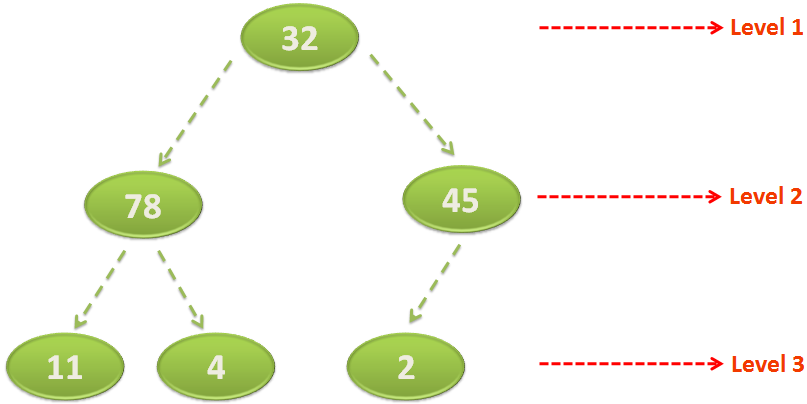
Let's take the bigger picture of the Binary Tree from the previous tutorial,

As we have seen, the 'buildHeap(...)' method calls 'void heapify(int arr[ ],int root, int length)' method.

Where the value of 'root' variable is 2.

So, we will be applying 'Heapify' on 32.

Just like the above explanation. We will compare left and right element.

if (left < length && right <= length && arr[right] < arr[left]) {

    smallest = right;
}
else if (left <= length){

    smallest = left;
}

But the thing to be noted is, there is no right element.

And this is when the condition 'left <= length' of 'else' statement comes into picture.

Where 'smallest' variable is directly initialised with the 'left' variable(Since, there is no right variable).

And the swapping happens and the 'heapify(...)' method ends.

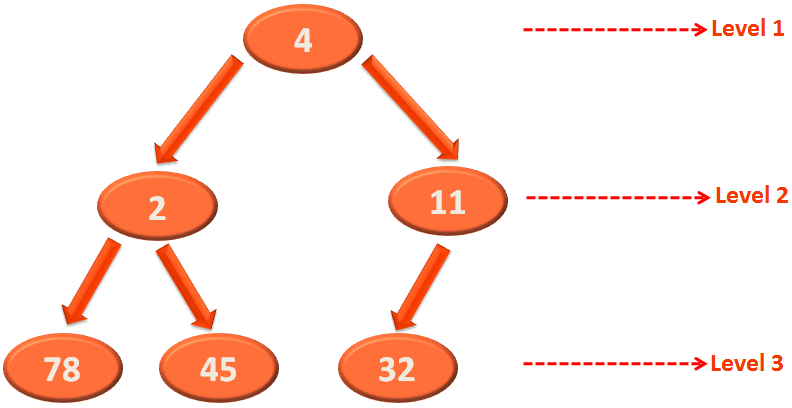
Again, control goes to 'buildHeap(...)' method and 'heapify(...)' is called again.

And 78 is dealt with.

Once again the swapping is done and control goes to 'buildHeap(...)' method.

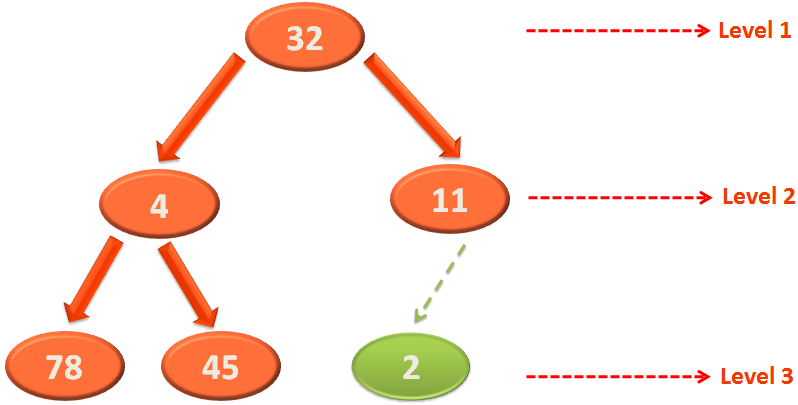
Now, the 'buildHeap(...)' method calls 'heapify(...)', dealing with the root element '4' finally.

As usual, we check if the left element i.e. 2 or the right element i.e. 11 is smaller and the swapping is done.

And the recursive call to 'heapify(...)' is made making 4 the root element. And no change is made.

And finally, we get a Heap.

Now, comes the deleteMin(...) method for sorting.

Let us discuss 'void deleteMin(int arr[ ])' method in detail :

  
public void deleteMin(int arr[]) {

    int len = arr.length-1;

    // Extract elements one by one from Heap
    for (int last=len; last>0; last--) {
            
        int temp = arr[0];
        arr[0] = arr[last];
        arr[last] = temp;

            
        heapify(arr, 0, last-1);
    }
}

Let us take the above Heap,

We will start with the last element and go till the top of the Heap.
```
for (int last=len; last>0; last--)
```

Then swap the root element i.e. arr[0] with the last element i.e. arr[last].
```
int temp = arr[0];
arr[0] = arr[last];
arr[last] = temp;
```
Now, if you look at the above structure, it is no longer a Heap(Since, the root element i.e 32 in Level 1 is greater than its children i.e. 4 and 11).

So we need to call 'heapify(...)' method.

Finally, we call the 'heapify(...)' method to convert the above structure to a Heap. But ignoring the last element as the last element (i.e. 2) will not be a part of heap anymore.
```
heapify(arr, 0, last-1);
```
'last-1' tells to ignore the last element.

And, after completing the loop we get the final array in descending order.

Running Time of Heap Sort

There is a three step process involved in Heap Sort :

Build a Heap.

Remove the Minimum element.

Use Heapify.

Now, if we analyse the running time.

Building a Heap can be done in O(n) time.

Removing the element takes O(log n) time.

Heapify takes O(log n) time.

Combining all the above running time, we get :

Total running time for Heap Sort : O(n log n)

❮❮ PREV NEXT ❯❯