What is the first thing that comes to your mind when you hear the term 'Tree'? Well ! Off Course, the 'Trees' all around us.
But in case of Algorithms, the concept of 'Tree' is sort of a family tree. i.e. A family tree can have a Parent, child, ancestor and so on. Kind of same concepts can be seen here.
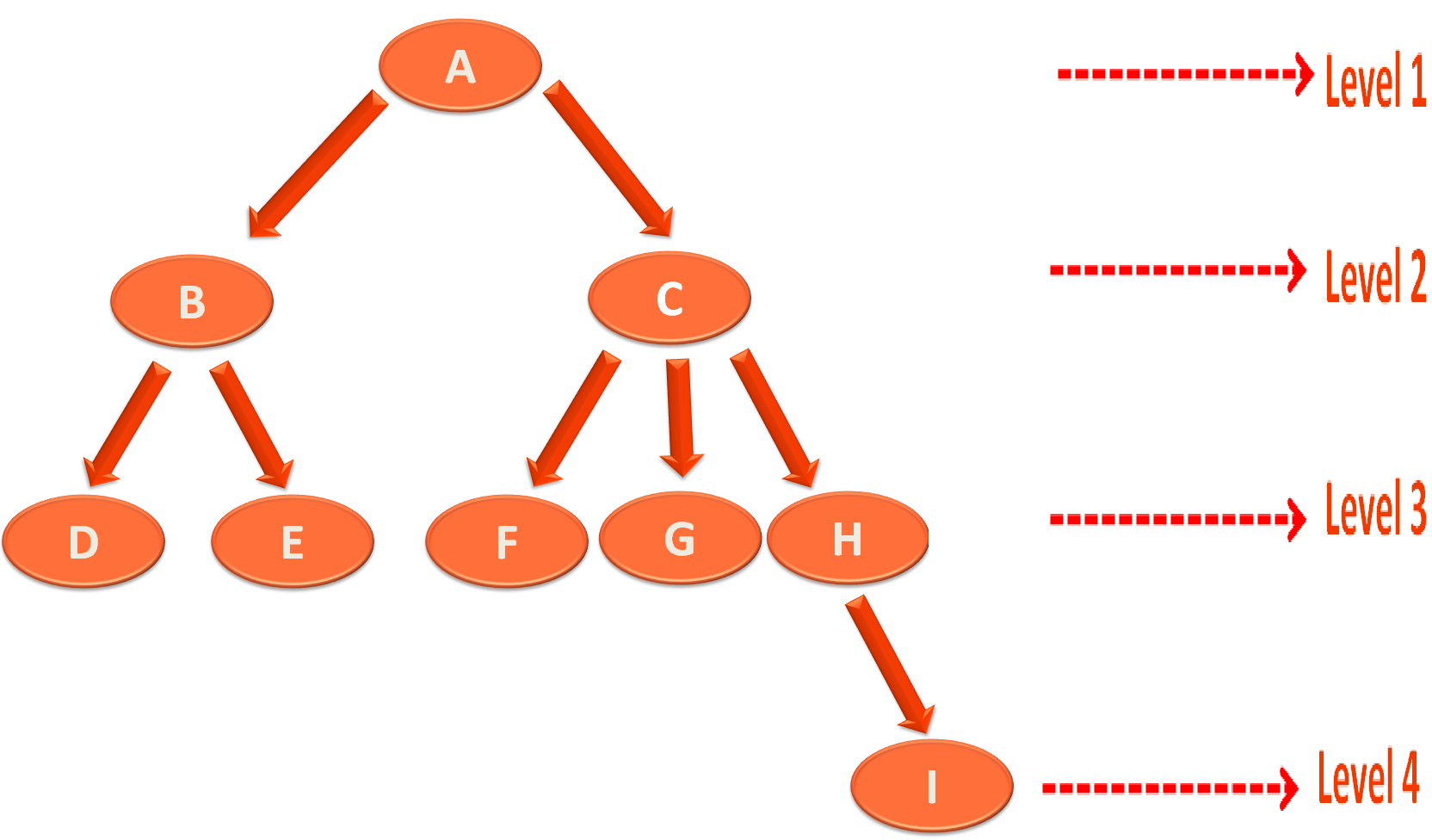
Let us understand some of the terms that are used in Tree :


