DFS - DEPTH FIRST SEARCH
DFS - Depth First Search for Undirected Graph
DFS - Depth First Search is also another Graph traversal algorithm that is quite easy to understand.
Let us understand with the same example we have used for BFS :
Say, you are a courier delivery guy and there are 5 cities (a, b, c, d and e) where you have to deliver the courier packages.
But your Boss is very strict and he doesn't want you to visit the same city twice.
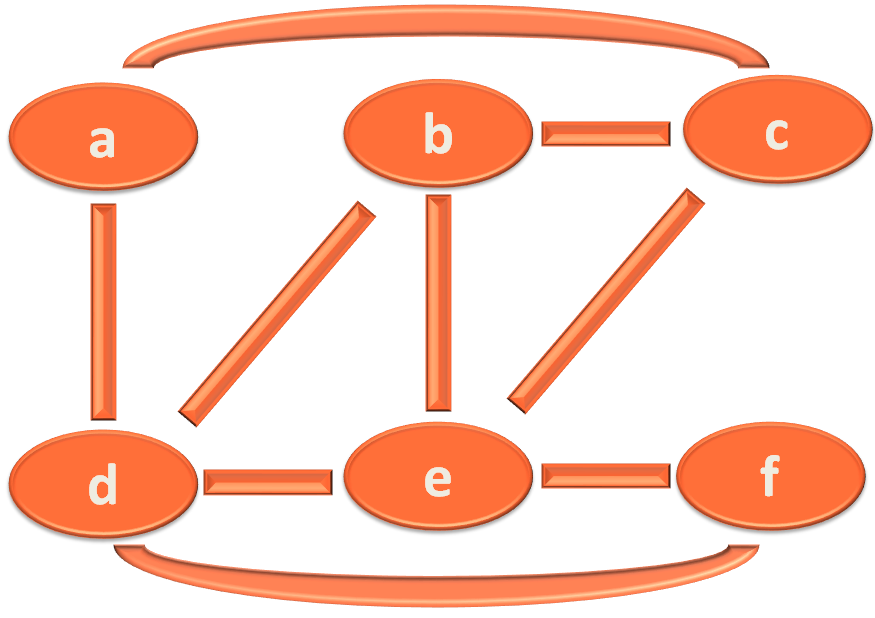
Below is the undirected Graph, which is also a roadmap that your Boss has given you.
So, as we can see there are 6 cities/vertices(a, b, c, d, e, f) and there are 9 edges/routes
Now, you will have to figure out a way to visit each city exactly once.
And this time we will use Depth first search (DFS) to solve the problem.
Now, for Depth first search (DFS) algorithm, you will need to follow the below steps :
Let's say, this time you are starting from City/Vertex 'a'. And you have to deliver packages to Cities/Vertices b, c, d, e and f.
You will just need a stack to maintain the order of the visited Vertices/Cities.
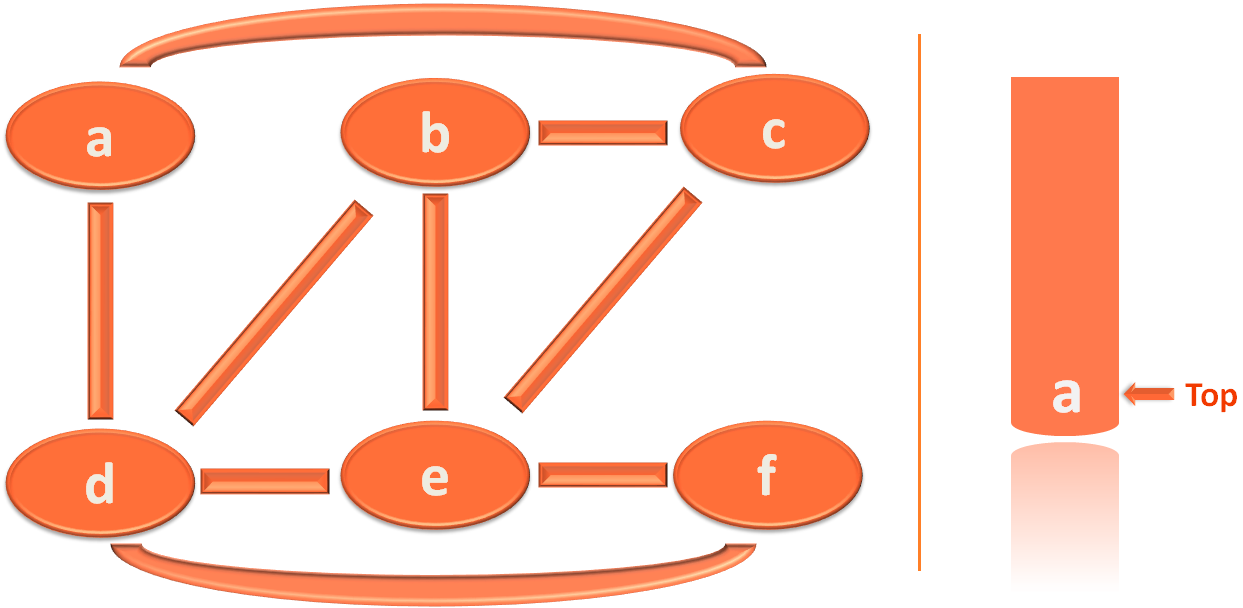
- So, the first thing you need to do is, mark 'a' as visited. But Why?
Simple answer, because we have already visited it.
And at the same time, place 'a' into the stack.
-
The next thing you need to do is, look at the stack and take the 'top' element(i.e. 'a').
Then try to find out the adjacent Vertices of 'a'(i.e. All the Vertices/Cities that are reachable from 'a'). They are 'c' and 'd'.
Now, you can either visit 'c' or 'd'.
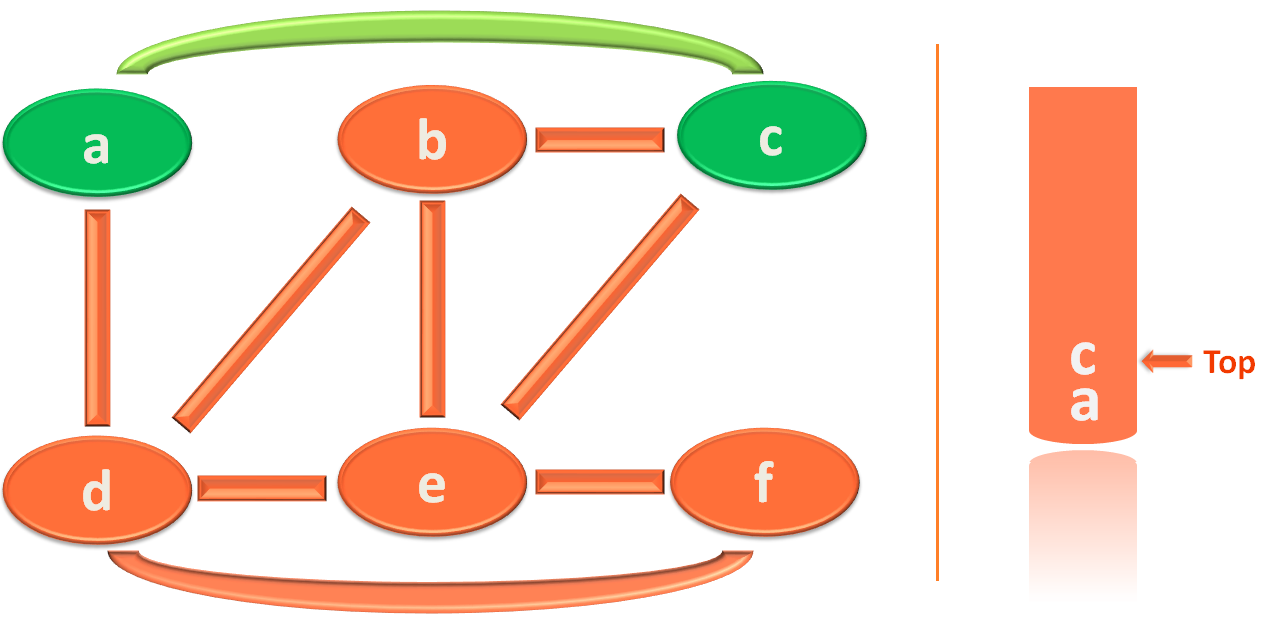
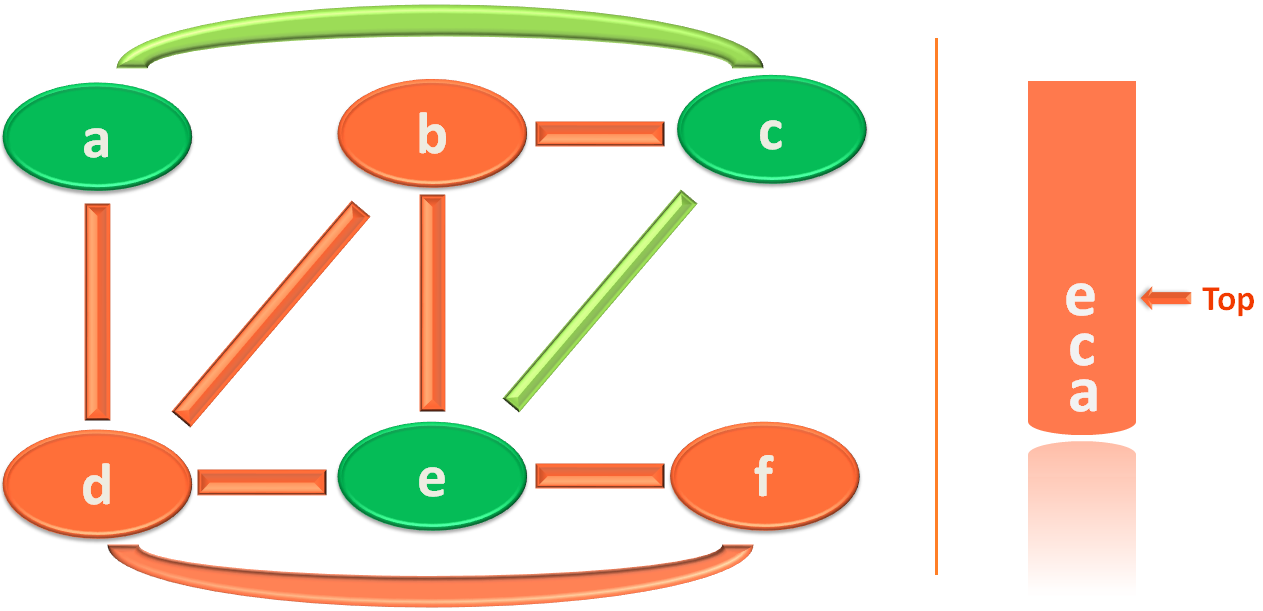
Let's say, you have chosen to visit the vertex 'c'.
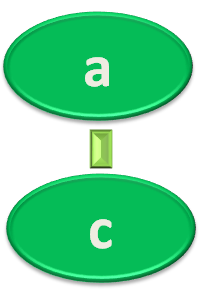
So, you visited 'c' and marked 'c' as visited. And placed it in the stack.
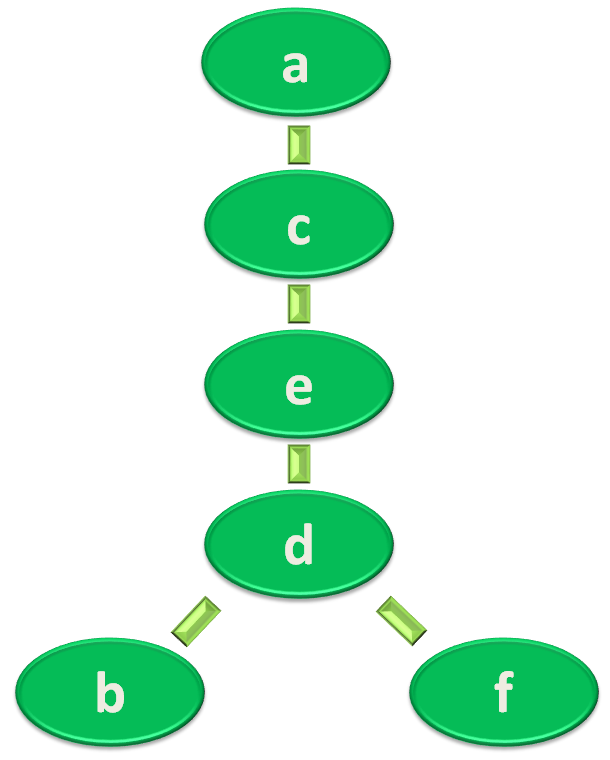
And currently the visited path is :
-
Next, you will repeat the same thing. i.e. Look at the Queue and take the top element ('c' is the top element). Then try to find out the adjacent Vertices of 'c'.
And, they are 'a', 'e' and 'b'.
Now, you can either visit 'a', 'e' or 'b'.
But, vertex 'a' is already visited. So, you need to choose from 'e' or 'b'.
Let's say, you have chosen to visit the vertex 'e'. And you marked 'e' as visited. And placed it in the stack.
So, currently the visited path is :
- Again, we will take the top element from the stack(i.e. e) and try finding the Adjacent Vertices of 'e'.
The Adjacent Vertices of 'e' are 'd', 'f', 'c' and 'b'.
But 'c' is already visited. So, you are left to choose from 'd', 'f' or 'b'.
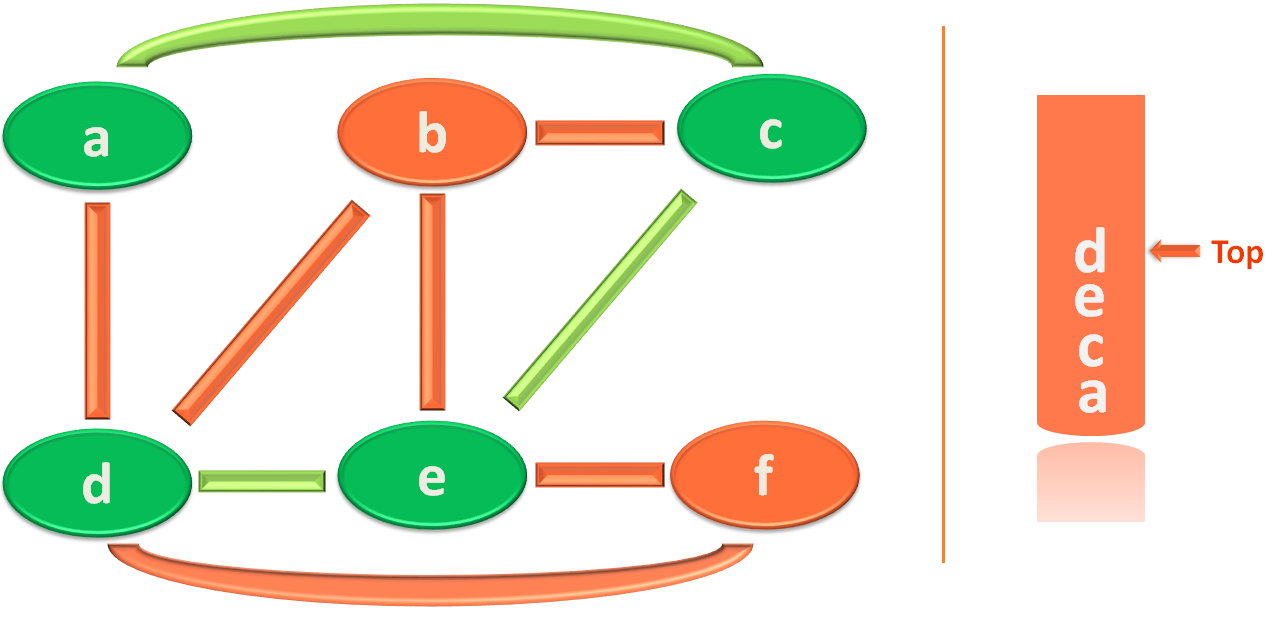
Say, you have chosen to visit the vertex 'd'. And you marked 'd' as visited. Also placed it in the stack.
And, the visited path is :
- Similarly, you will take the top element from the stack(i.e. d) and try finding the Adjacent Vertices of 'd'.
The Adjacent Vertices of 'd' are 'a', 'b', 'e' and 'f'.
Among which vertices 'a' and 'e' are already visited.
So, you are left to choose from 'b' or 'f'.
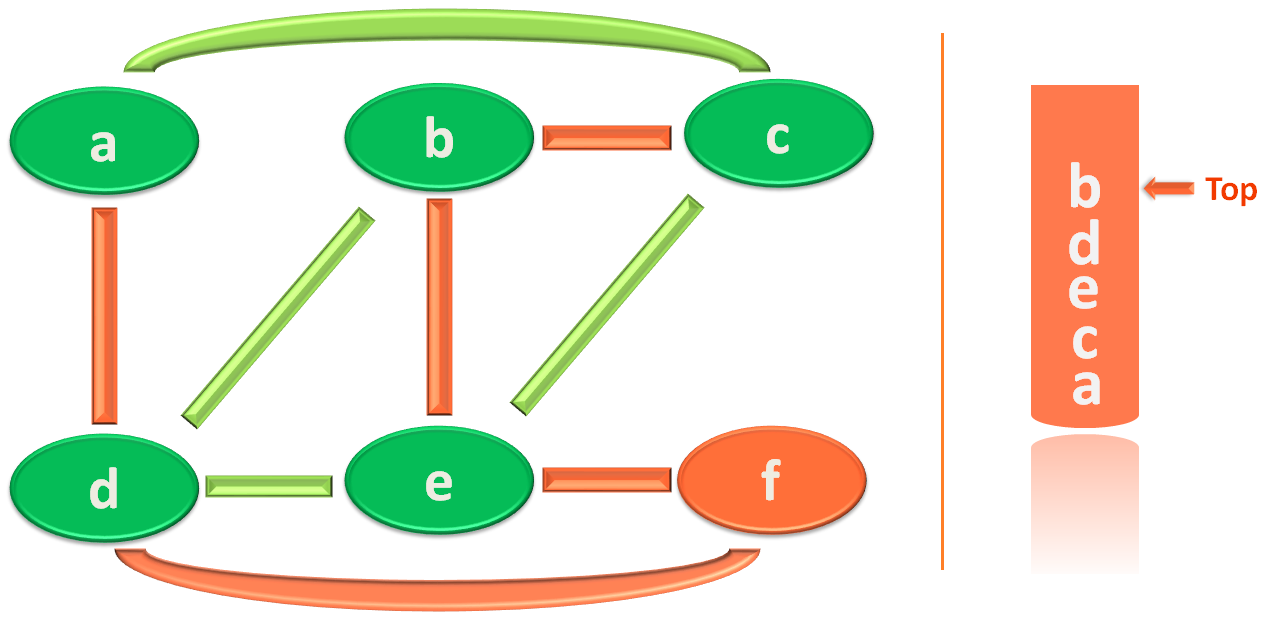
And, you have chosen to visit the vertex 'b'. And you marked 'b' as visited. Also placed it in the stack.
And, the visited path is:
- Once again, you will take the top element from the stack( i.e. b) and try finding the Adjacent Vertices of 'b'.
The Adjacent Vertices of 'b' are 'c', 'e' and 'd'.
But, the vertices 'c', 'e' and 'd' are all visited.
So, you have no city/vertex to visit.
But the question is, the city/vertex 'f' is not yet visited!
And this is where Backtracking comes into picture. Backtracking is, to go back in the same track you came from.
So, how do you backtrack here?
And this is where, the stack comes handy. As the stack, keeps track of the order of the visited vertices.
Let's see how!
Now, since all the Adjacent vertices of vertex 'b' are visited. We will pop out 'b' from the stack.
And, still the visited path is :
- Now, if you see the top element of the stack, it is the vertex 'd'.
And 'd' was visited just before you have visited 'b'. So, thanks to the stack, it helped us backtrack.
Now, we repeat the same process. i.e. Try to find the Adjacent vertices of 'd'( i.e. the top element of stack).
The Adjacent Vertices of 'd' are 'a', 'b', 'e' and 'f'.
Among which vertices 'a', 'b' and 'e' are already visited.
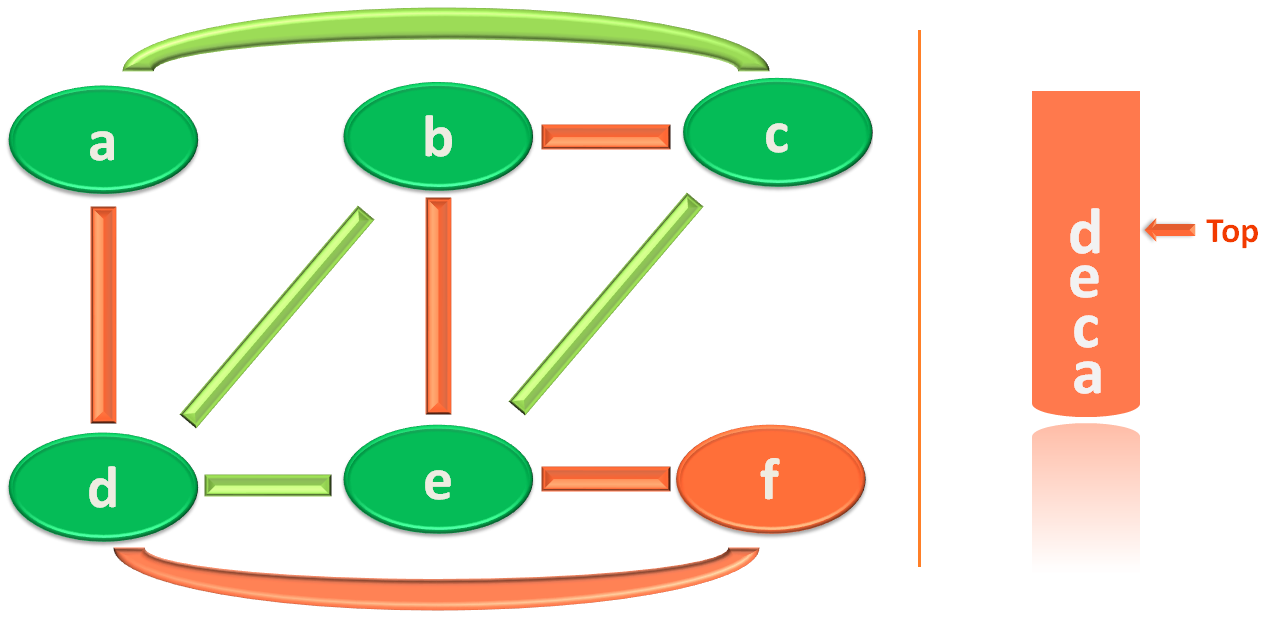
And Yay! We are left with 'f'.
And you marked 'f' as visited. Also placed it in the stack.
And, the visited path is :
Now, if we look at the diagram, we can see that all the nodes are visited.
But the logic is to continue the process until the stack is completely empty.
So, we take the top element of the queue(i.e. f) and check if all the adjacent vertices of 'f' are visited or not.
And as we know, all the adjacent vertices of 'f'(i.e. d and e) are visited. So, we pop 'f' out of the stack.
Similarly, we will check if the adjacent vertices of the top element 'd' is visited or not. And we found that all are visited.
Similarly, we pop all the element until the stack is empty.
And, the actual path traversed using Depth First Search (DFS) is :
Note : There are two ways we can implement Depth First Search (DFS). First is the Iterative approach and the second approach is the Recursive approach. The recursive approach is where java create and maintains the above stack all by itself and is quite popular. And the Iterative approach is where we need to create and maintain the stack ourself.
Time complexity for Depth First Search (DFS) :
O(V + E)
Where V is the number of vertices and E is the number of edges in the graph.
Space Complexity for Depth First Search (DFS) :
O(V)
Where V is the number of vertices.
We will see the implementations of Depth First Search (DFS) in the next tutorial.