So, far we have looked at Binary Trees(i.e. A tree that can have maximum 2 children).
Now, we will use the Binary Trees and tweak its feature a little, so that it becomes quite effective for searching an element in it. And will call it a 'Binary Search Tree'.
The Binary Search Tree has two important properties :
Let us understand the above properties with the below example,
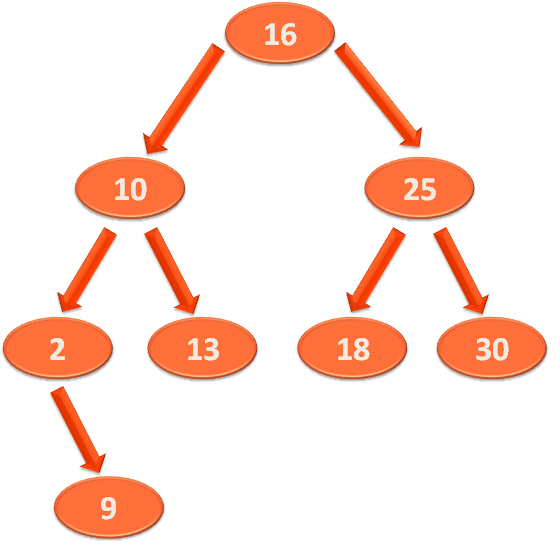
As we can see that '16' is the root element.
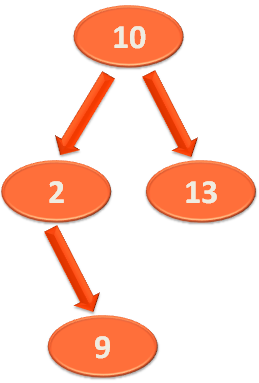
And the Left Sub-Tree of '16' is :
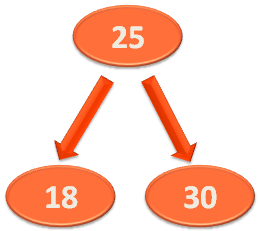
And the Right Sub-Tree of '16' is :
Now, according the first property, all Nodes in the Left Sub-Tree must be less than the Root element and the Right Sub-Tree.
So, let us pick any element from the Left Sub-Tree. Say, we have picked the element '13'.

Now, if we compare '13' with the root element '18'. We can see that '13' is less.
Similarly, if we compare '13' with all the elements of the Right Sub-Tree. There are three elements 25, 18 and 30.

And '13' is less than all the three elements of the Right Sub-Tree.
Now since, we have checked the first property. Let us check the second property, i.e. All Nodes in the Right Sub-Tree must be greater than the Root element and the Left Sub-Tree.
So, as usual, let us pick any element from the Right Sub-Tree.
The Right Sub-Tree is,

Let us take the element '18'. And let us compare '18' with the root element '16'.
And '18' is greater than the root element '16'.
Now, let us compare '18' with the elements of the Left Sub-Tree. The elements in the Left Sub-Tree are 10, 2 9 and 13.

And '18' is greater than all the elements of the Left Sub-Tree.
Now, let us take any Sub-Tree. Say, we will take the Right Sub-Tree.

Now, if we consider '10' as the root element. All the elements of the Left Sub-Tree (i.e. 2 and 9) is less than '10'.
And the element in the Right Sub-Tree(i.e. 13) is greater than the root element '10'.
So, above properties applies to the the entire 'Binary Search Tree'.
Let us take the same Binary Search Tree to find the Smallest and Largest element.

The Smallest element is always at the end of the left most Sub-Tree i.e. 2.

And the Largest element is always at the end of the right most Sub-Tree i.e. 30.

So, we have the below Binary Search Tree :

Now, let us say, we will try inserting the element '3' to the above Binary Search Tree.
And as per the properties of the Binary Search Tree, all elements less than the root element should be on the left Sub-Tree and all elements greater than the root element should be on the right Sub-Tree.
With these properties in mind, let us try inserting the element '3' to the Binary Search Tree.
So, the first thing we do is, compare '3' with the root element '16'.
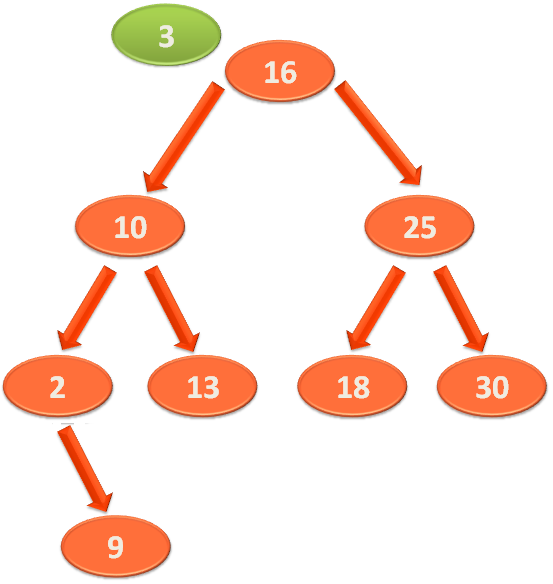
And find that '3' is less than '16'. So, as per the property of the Binary Search Tree, '3' should be somewhere in the Left Sub-Tree.
And we compare '3' with the first element of the Left Sub-Tree i.e. 10.
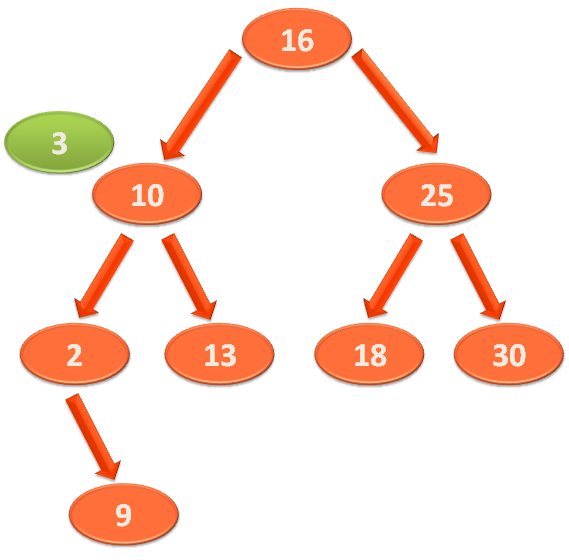
Even in this case we find that '3' is less than '10'. So, '3' should sit somewhere in the Left Sub-Tree of '10'.
And the first element in the Left Sub-Tree of '10' is '2'.
So, we compare '3' with '2'.
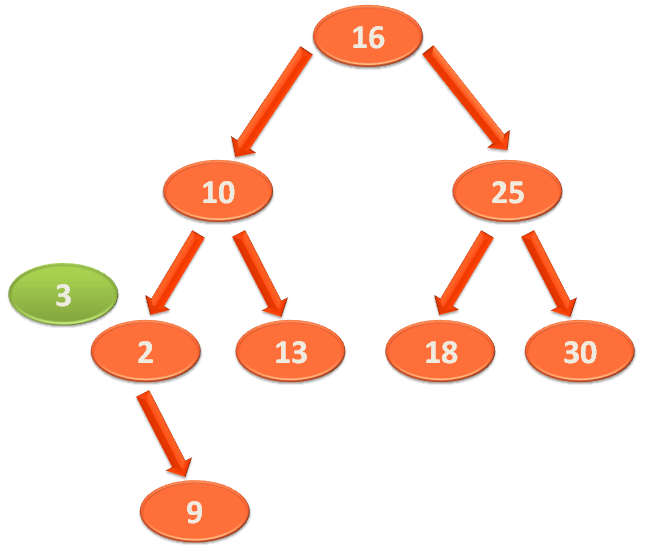
Now, in this case, '3' is greater than '2'. So, it will sit somewhere in the Right Sub-Tree of '2'.
And the first element in the Right Sub-Tree of '2' is '9'.
So, we compare '3' with '9'.
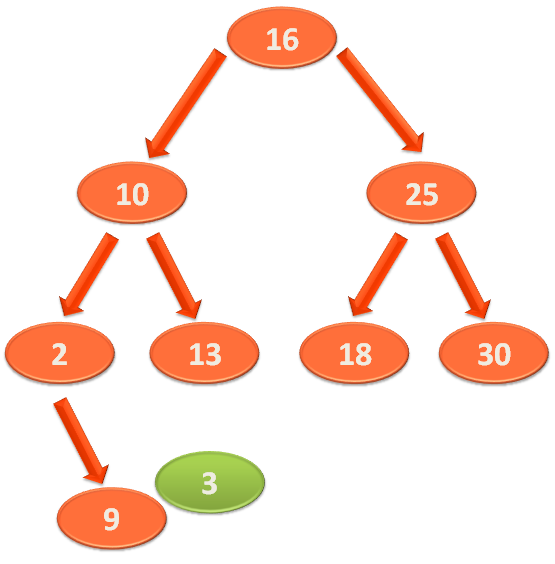
In this case we find that '3' is less than '9'. So, it sit somewhere to the left side of '9'.
And since, there is no elements in the left side of '9'.
So, '3' goes and sits there finally.
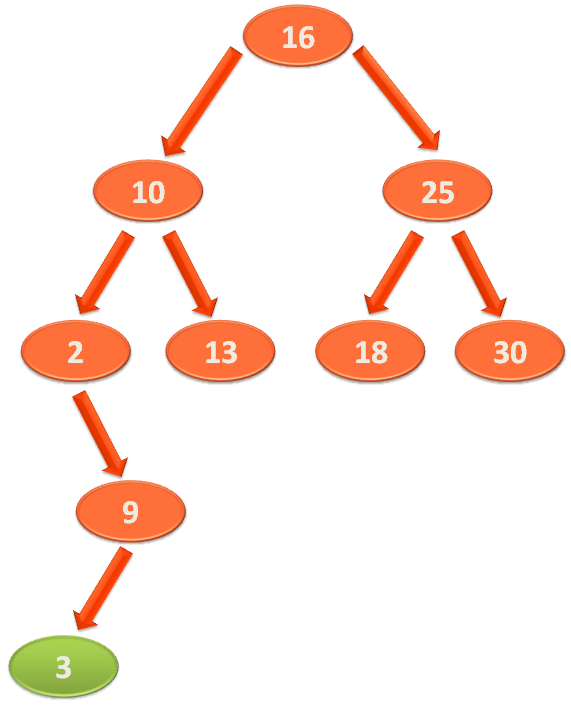
So, we have the below Binary Search Tree :

Let us say, we want to delete the element '18' from the above Binary Search Tree.

Now since, '18' has no children, it can be deleted and no further adjustments needs to be done in the above Binary Search Tree.

Next, let us say we want to delete the root element '16'.
So, we will delete the root element '16' first.
Now, the question would be, who would fill the place of the deleted root element i.e. '16'?
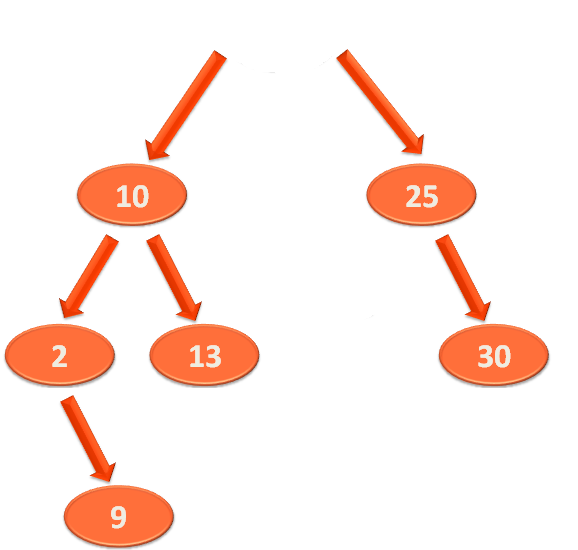
Now, let us take the element from the Left Sub-Tree to fill its place. So, as we know that all the elements that are less than the root element are on the Left Sub-Tree.
Below is the Left Sub-Tree :

Now, if we take the largest element from the above Left Sub-Tree and place it as the root element.
So in this case, the root element of the above Left Sub-Tree is '10'. And as we know all the elements at the right of the Binary Search Tree should be greater than the root.
And since, there is just one element in the Right Sub-Tree of 10 i.e. '13'. So, '13' can be placed at the place of the root element.
And '13' is called as the 'Inorder Successor'.
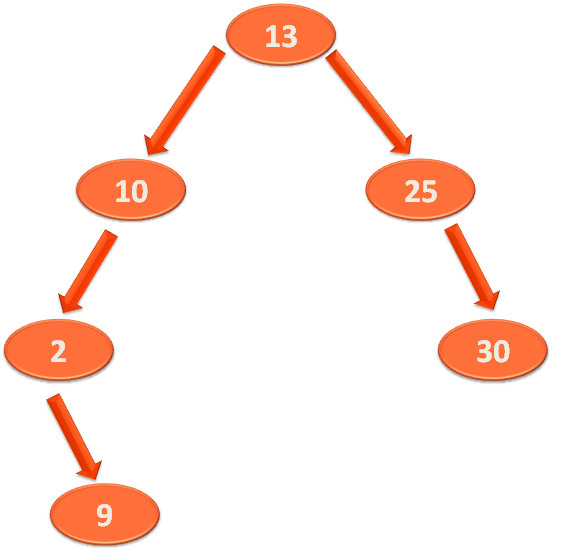
Once again, let us take the below Binary Search Tree,

Let us say, we want to search the element '2' from the above Binary Search Tree.
So, as we have done in the above case, we would compare the element '2' with the root element '16'.
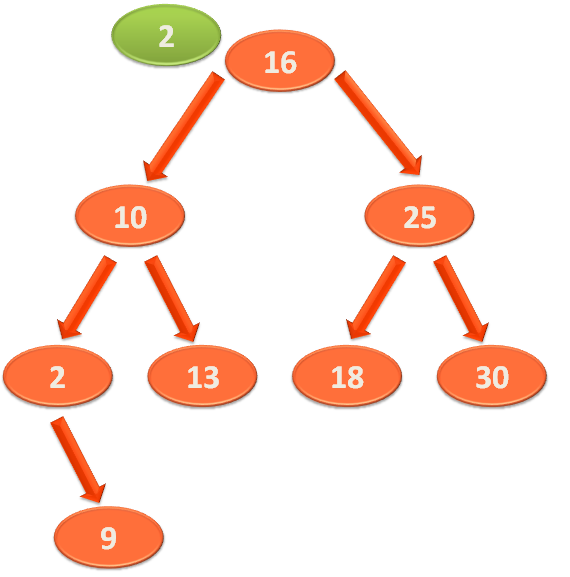
And find that '2' is less than '16'. So, the element '2' should be somewhere in the Left Sub-Tree.
So, we would compare '2' with the first element of the Left Sub-Tree i.e. 10.
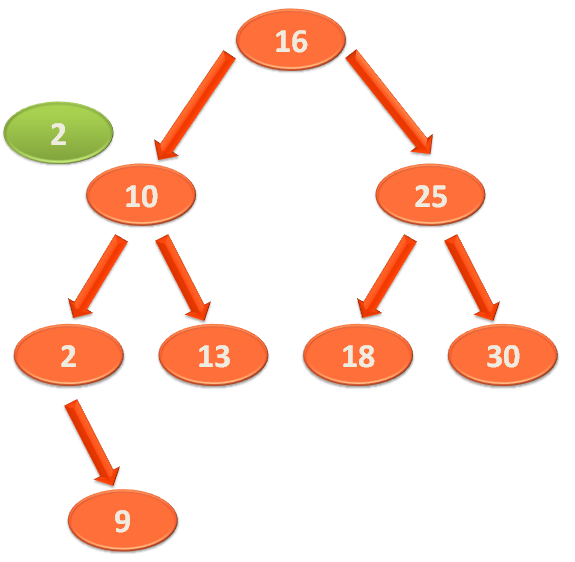
Now, '2' is less than '10'. So, '2' should be somewhere in the Left Sub-Tree of '10'.
So, we compare '2' with the first element of the Left Sub-Tree of '10'.
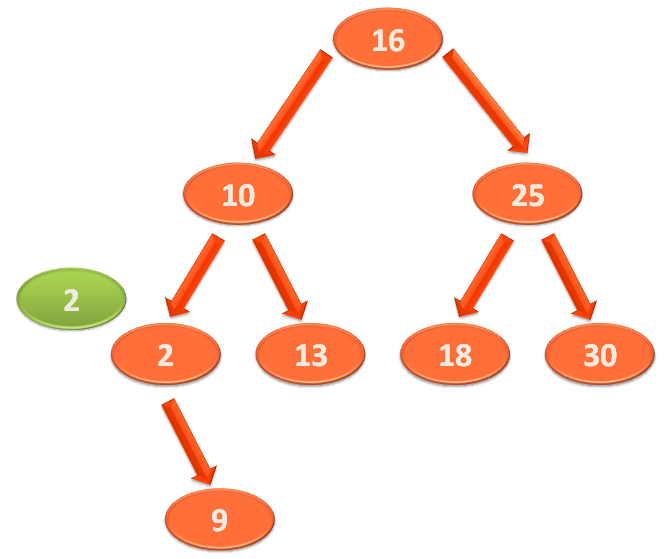
And the first element of the Left Sub-Tree of '10' is '2'. So, we find the element '2' in this location. And our search is complete.
Best Case to Insert an element in Binary Search Tree : O(log n)
Average Case to Insert an element in Binary Search Tree : O(log n)
Worst Case to Insert an element in Binary Search Tree : O(n)
Best Case to Delete an element from Binary Search Tree : O(log n)
Average Case to Delete an element from Binary Search Tree : O(log n)
Worst Case to Delete an element from Binary Search Tree : O(n)
Best Case to Search an element in Binary Search Tree : O(log n)
Average Case to Search an element in Binary Search Tree : O(log n)
Worst Case to Search an element in Binary Search Tree : O(n)