❮❮ PREV NEXT ❯❯

MERGE SORT

Merge Sort is an efficient algorithm that works on Divide and Conquer strategy. It might look a little complex than Bubble Sort or Insertion Sort. But no worries, we will make it as simple as Bubble Sort or Insertion Sort.

Note :Divide and Conquer is to divide a list into smaller parts. Then work on those smaller parts (Maybe you can perform a sorting on those parts) and merge them back.

As said, Merge Sort works on Divide and Conquer strategy. Just think Divide and Conquer strategy is to keep on dividing a list into approximately two equal halfs until there is only one element left in each divided list. And then comes the Conquer step, where we start combining the lists after sorting them.

Just remember that its a three step process :

Divide : We divide a list of size N(Say size is 4) into two equal halfs, n1 (So its size should be 2) and n2 (Even its size should be 2 as well).
Conquer : Then sort the lists n1 and n2 separately.
Combine/Merge : Then combine n1 and n2 again after sorting them.

Already looks complicated !! Let us simplify this with an example,

Example :

Let us say there are 4 elements in a list and we need to sort them in ascending order.

So, at first it is the DIVIDE step. And we go on dividing each part, until there is only one element left in the list.

Divide

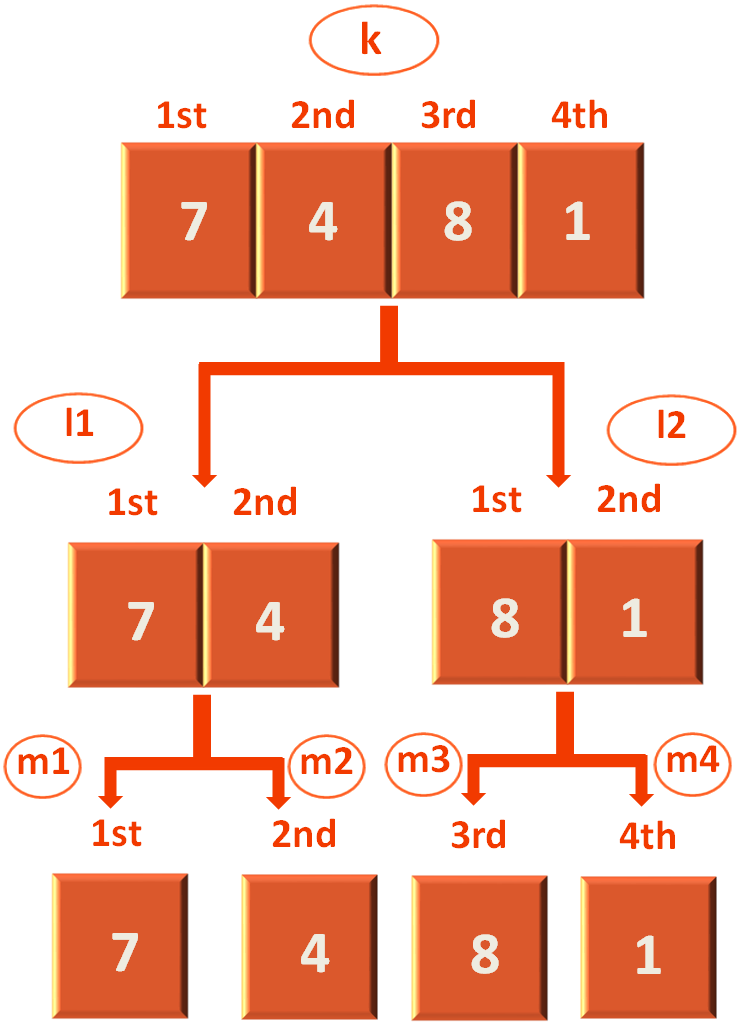
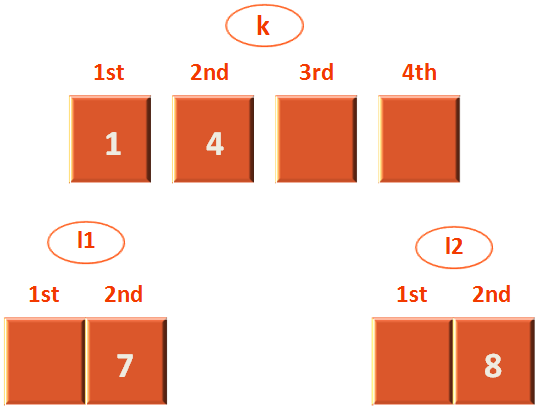
Now, as said we will divide the above list 'k' into two equal parts. So, that each part contains 2 elements each.

Now, we have 2 lists l1 and l2. And we have to subdivide l1 & l2 again as, we have to keep on subdividing the lists until we have 1 element in each list.

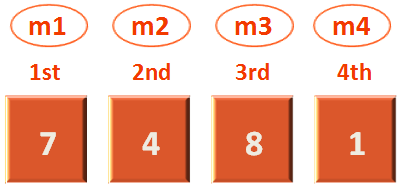
Finally, we are done with the divide step. As each list m1, m2, m3 and m4 contains one element each.

Now, it is time to CONQUER.

Conquer

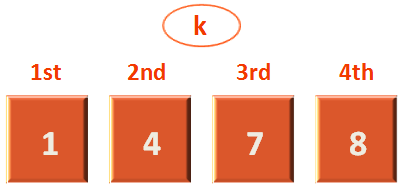
Now, let us look at the entire diagram and see, how the list is divided.

In Conquer step we will start from the very left and sort individual lists.

The very left element is

And since there is only one element in the list, we can assume that the above list is already sorted.

Similarly,

Also contains just one element and we can assume the above list is also sorted.

Now, it's time to COMBINE/MERGE.

Combine / Merge

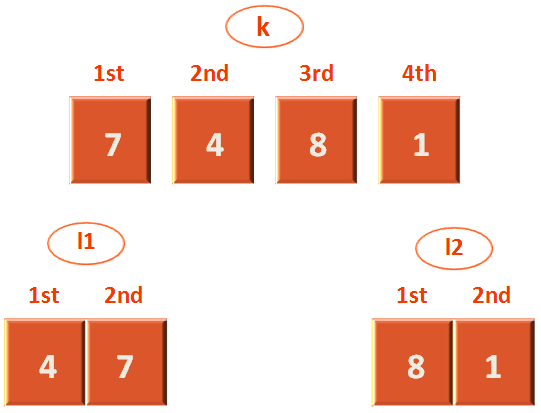
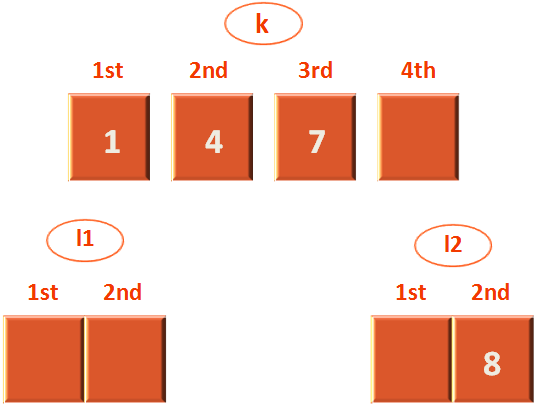
So, we need to Combine/Merge 7 and 4 back to the sublist from which it was divided(Off course after sorting them).

And, the immediate list from where 7 and 4 got subdivided is,

So, we check if the element in the m1 list is less than the element in the m2 list. And we find 7 in greater than 4. So, we swap the positions of 7 and 4 and put them back to the list l1.

Now, the new list becomes,

And we can discard the lists m1 and m2.

And, the list l1 is sorted.

So, we try going up and find the list k has one more sublist l2(Which is not yet sorted).

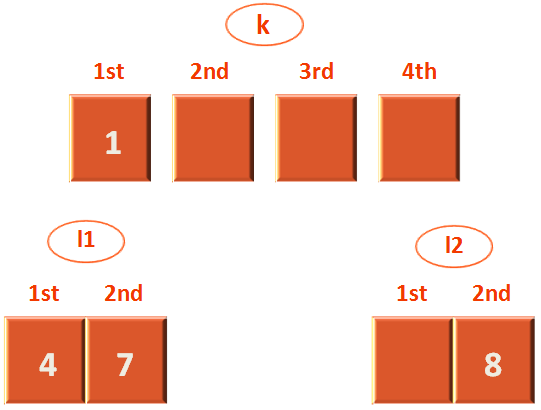
Now, let us take the sublist l2,

Now, it is the Conquer step where we intend to sort the lists m3 and m4,

Conquer

Since, the lists m3 and m4 has only one elements each, it is considered to be sorted.

Now, we combine/merge them.

COMBINE / MERGE

So, we check if the element in the m3 list is less than the element in the m4 list. And we find 8 in greater than 1. So, we swap the positions of 8 and 1 and put them back to the list l2.

Now, the new list becomes,

So, we can say that l1 and l2 is sorted.

Now, it's time we take a look at the main list k.

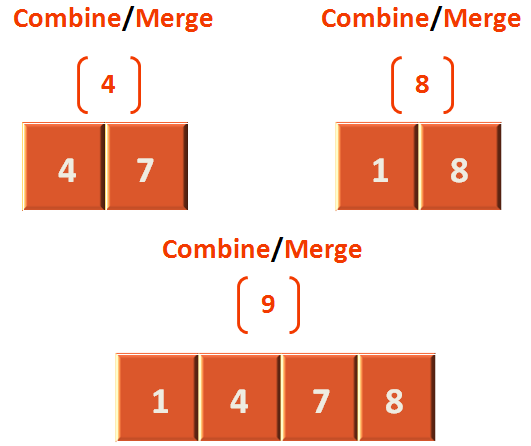
Since, l1 and l2 is sorted it's time to Combine/Merge l1 and l2 with the main list k.

COMBINE / MERGE

Now, we need to Combine/Merge list l1 and l2 back to the main list k from which it was divided.

Note : And, don't forget that we have to sort the list l1 and l2 before merging it with the main list k.

Now, comes the main part.

We need to compare the first elements of lists l1 and l2. And, why is that? Because lists l1 and l2 are already sorted. So, the smallest element in the list l1 is 4 and the smallest element in list l2 is 1. If we compare these two elements, we get the smallest element.

So, we check if 1st element of l1 i.e. 4 is greater than the 1st element of l2 i.e. 1. And find 4 is greater than 1. So, we take '1' from list l2, and place it in the 1st location of list k.

So, 1 from list l2 goes and sits in the 1st position of list k.

Now, as we can see the first location of the list l2 is vacant. So, in the next step we compare the 1st element of l1 i.e. 4 with the 2nd element of list l2 i.e. 8(We compare with the second element of l2 as the 1st location of l2 is vacant).

And, we see 4 is less than 8. So, we take the first element of l1 i.e. 4 and place it in the 2nd location of the main list k.

Then we are left with the 2nd element of l1 i.e. 7 and the 2nd element of l2 i.e. 8. And when we compare them, we found 7 is less than 8. So, we take 7 from the 2nd location of l1 and place it in the 3rd location of the main list k.

And finally, we are only left with the 2nd element of list l2 i.e. 8. So, we take it and place in the 4th location of list k.

And the list k is sorted. So, we can discard the list l1 and l2.

Now, since we have understood the way Merge Sort Algorithm works. Let us understand the bigger picture from coding perspective.

Here, we will go all the way down to the left, breaking the list and come up by merging it.Let's see how?

As in the diagram, in step (1) we can see the left list has two elements i.e. 7 and 4 in unsorted order. And we divide it into two parts.
Next, in step (2) we have taken the left half which has only one element i.e. 7. Since, the list has one element, we don't have to divide it further.
Then, we take the other half i.e. 4 in step (3).
Now, it's time to Combine/Merge in step (4). And we merge 4 and 7 after comparing them with each other. So, the left half of the main list is sorted now.
Since, the left half of the main list is sorted. It's time to consider the right half of the main list in step 5. And the list has two elements 8 and 1, unsorted. Which we need to divide into two parts.
So, we take the left half in step (6) which has only one element i.e. 8. And the list doesn't have to be divided further.
Next, we go to the right half in step (7), which also has one element i.e. 1.
Now, it's time to Combine/Merge in step (8). And we merge 1 and 8 after comparing them with each other. So, the right half of the main list is also sorted now.
And we are in the final step (9). Where we combine both the lists after comparing them with each other. And we get the sorted list.

❮❮ PREV NEXT ❯❯