❮❮ PREV NEXT ❯❯

HEAP SORT

To understand Heap Sort, you need go through the 'Heap' tutorial.

As we will be using the terms like,

Building a Heap

Delete the minimum element from a Heap

Heapify

Note : Feeling lazy to go back and learn the above topics. No worries, we will explain them in brief.

So, to implement Heap Sort, we will be following the below steps :

We will build a Heap from the given elements.

We keep on deleting the minimum element until the Heap becomes empty. But the fun fact is, we don't delete the minimum element. Instead we keep on putting the minimum elements at the end of the array, until we get all the elements in descending order.

Let us clarify using the below example :

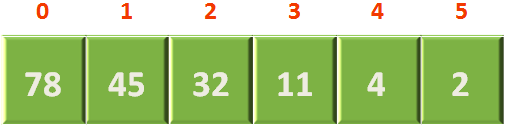
We are given a list of 6 numbers,

4, 78, 32, 2, 45, 11.

So, the first step is to create a Heap.

Note : If you have read, 'Building a Heap' from Heap tutorial. You can skip the below two step process of creating a Heap.

Let's, follow the below steps to create a Heap :

We will form a binary tree with the following numbers.

What we have done is, taken the first element 4 and placed it in the root element(In Level 1). Then we have taken the second and third element 78 and 32 and placed it as left and right child of the root element(In Level 2).

And, similarly Level 3 is filled.

Next, we will use Heapify to transform the above binary tree to a Heap.

Now, the condition of Heapify is, the children of the Node on which Heapify is applied,must be a Heap.

So, let us take the last Level(i.e. Level 3). Now, since there are no children of the elements of Level 3(i.e. 2, 45 and 11). We can consider 2, 45 and 11 satisfies the property of Heap.

Now, let us come to Level 2. We can apply Heapify on 78(As both of its children 2 and 45) can be considered as Heap.

After applying Heapify on 78, we get,

Similarly, we will apply Heapify on 32 of Level 2. And get the below result.

Now, we can apply Heapify on the root element i.e.4. As both of its children 2 and 11 are Heaps.

After applying Heapify, we get,

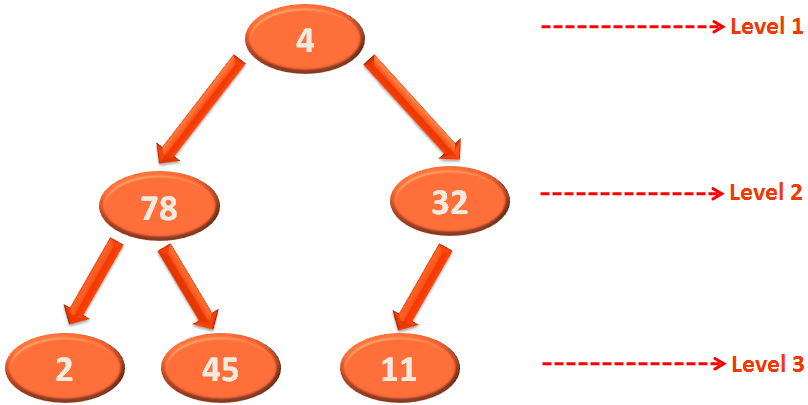
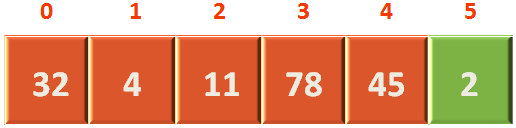
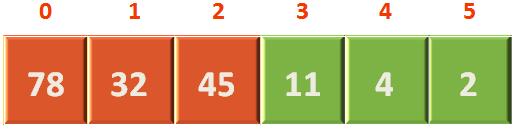
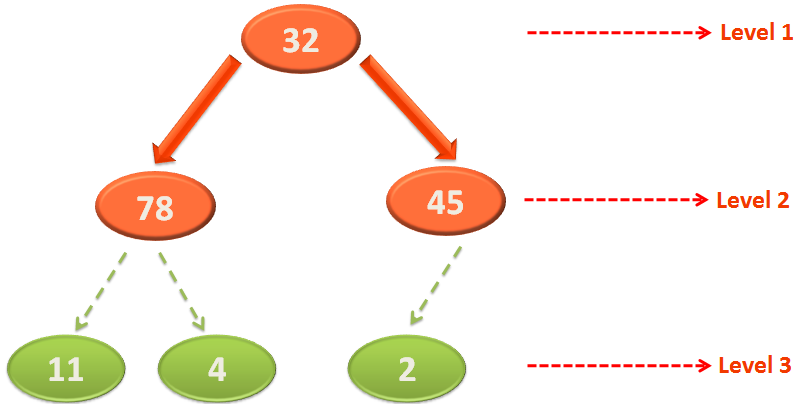
Now, since we have build the Heap. Let us represent it in the form of an array to understand better.

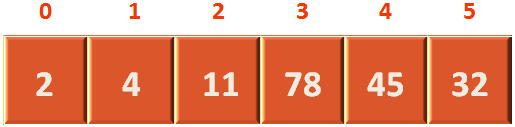
Creating the above array is quite simple.

We take the root element 2 and place it in the 1st location of the array.

Similarly, take the elements 4 and 11 from Level 2 and place it in the 2nd and 3rd location of the array. And so on.

Now, it's time to apply the 'Delete Min' feature. i.e. Keep on removing the minimum element and placing them at the end of the Heap.

Now, as we know that the minimum element is the root element of the Heap.

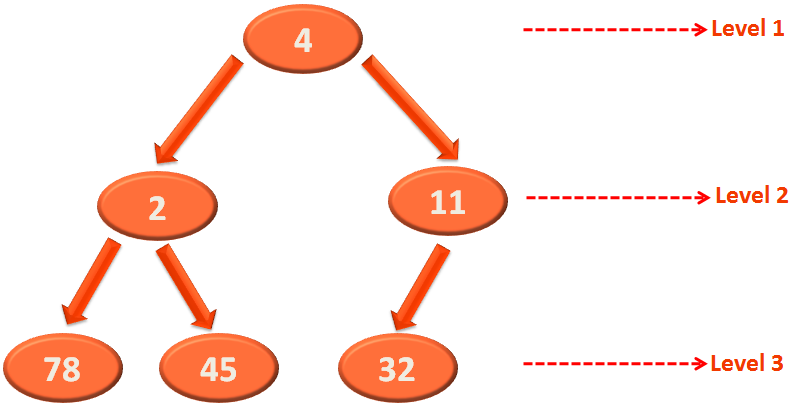
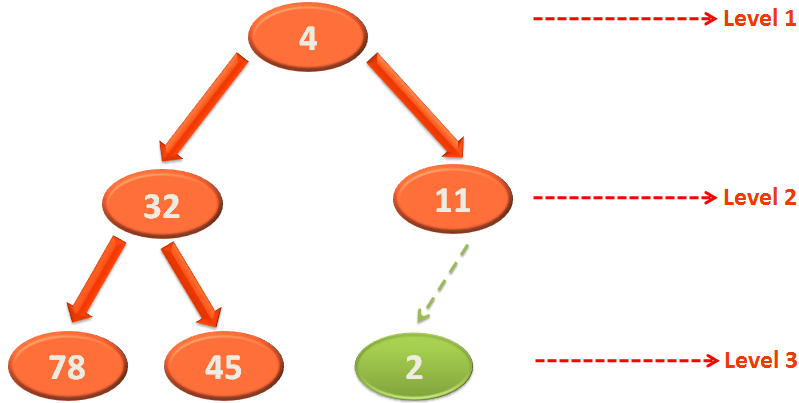
So, take the minimum element i.e. 2 and swap it with the last element of the Heap i.e. 32.

Note : The important point to note is, we will consider that 2 is no longer there in the Heap.As it is already removed from the Heap.

Now, the Heap doesn't satisfy the structural property. i.e. 32 is greater than its children 4 and 11.

And since the children of 32 i.e. 4 and 11 are already Heaps. We can apply Heapify on 32.

Note : The last node i.e. is not a part of Heap anymore.

After applying Heapify on 32,

So, we got a Heap again.

Now, let's apply 'Delete-Min' on it.

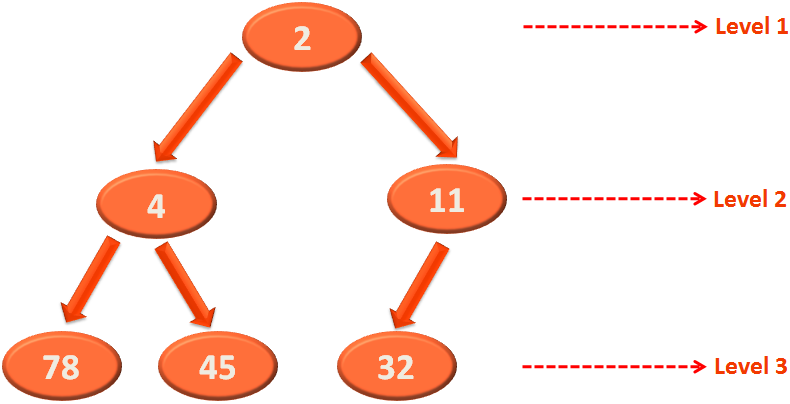
Since, the root element is the minimum element. Let's swap it with the last element i.e. 45(As 2 is not a part of Heap anymore).

Note : Now, both 4 and 2 are not part of the Heap anymore.

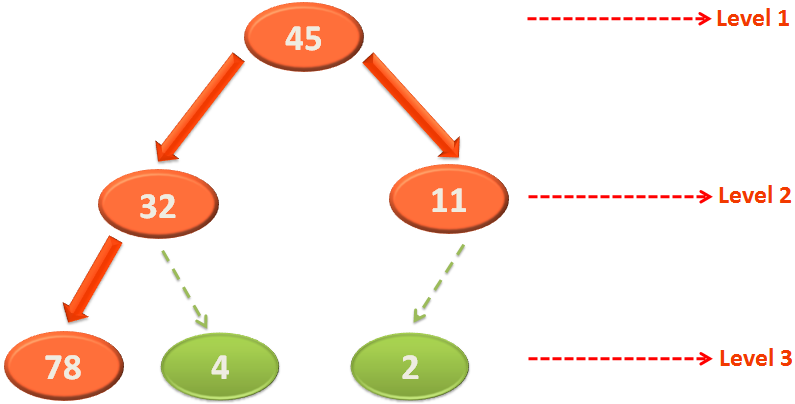
Again, the above structure is not a Heap.

Let's apply Heapify on the root node 45.

Since, both the children of 45 i.e. 32 and 11 are Heaps. We can use Heapify on 45.

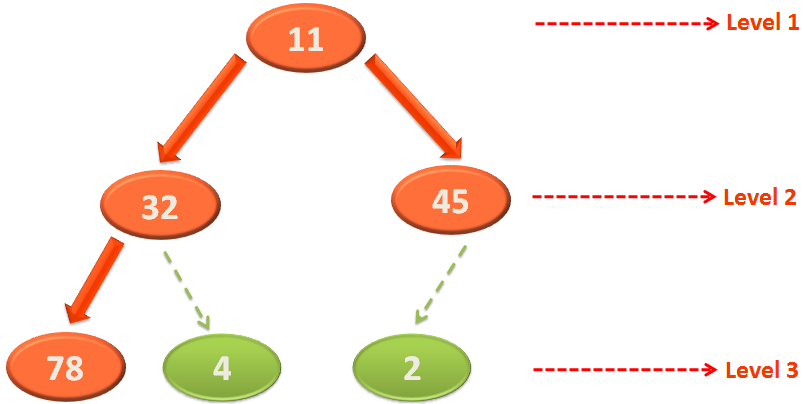
We got a Heap now. So, let's apply 'Min-Heap'.

Note : 11, 4 and 2 are not part of Heap anymore.

Let's apply Heapify on 78 to make it a Heap.

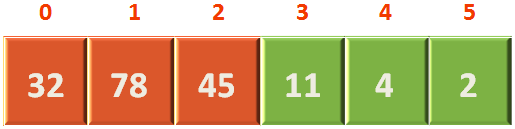
If we continue the same process until there is no element left. We get the below Heap.

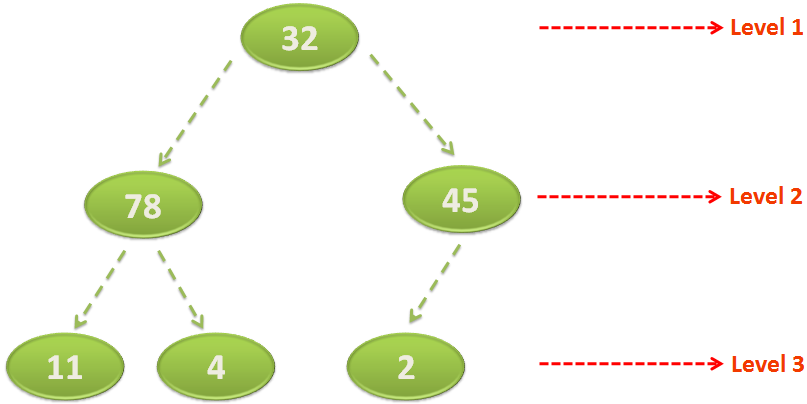
And if we look at the final Heap, we got the Heap in descending order.

Running Time of Heap Sort

There is a three step process involved in Heap Sort :

Build a Heap.

Remove the Minimum element.

Use Heapify.

There is a three step process involved in Heap Sort :

Building a Heap can be done in O(n) time.

Removing the element takes O(log n) time.

Heapify takes O(log n) time.

Combining all the above running time, we get :

Total running time for Heap Sort : O(n log n)

❮❮ PREV NEXT ❯❯