LINEAR SEARCH

Linear Search is the simplest algorithm available.

It starts searching an element from the very first location and then second then third, and continues until it finds the element.

Let us try understanding with a real life example :

Say you are a class teacher and you are told by somebody that one of the student in your class has brought a mobile phone in the classroom.

For simplicity, let's say, only there are only 5 students in your class. All sitting in a single row.

What would you do to catch that particular student?

You would start with the 1st student, and check his bag. Then come to the 2nd student and check his bag. And go on searching until you find the student who has the mobile phone in his/her bag.

And the same theory applies for 'Linear Search'.

Let us take the below example :

We have the below array, consisting 6 elements. Now, we are asked to find the element '2' from the array.

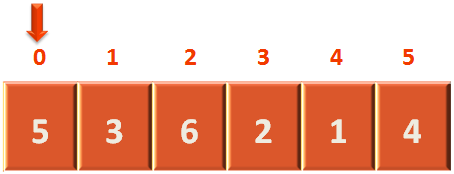
So, we start with the first element in the array and check, if '2' is present in the first location or not.

Since, the first element is '5'. We move to the second location.

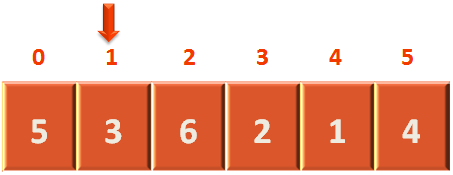
Even in the second location, the element 2 is not present. So, we move to the third location.

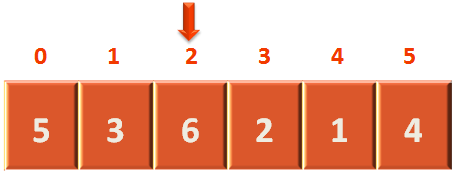
In the third location, the element is 6. So, the element 2 is not present, even in this location.

So, we move to the fourth location.

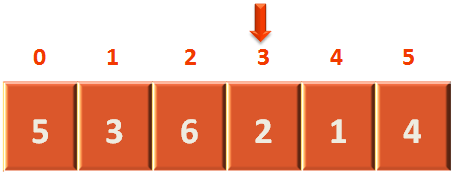
Finally, we found that the element '2' is present in the fourth location or array index '3'.

So, this is how 'Linear Search' works on finding an element.

Running Time of Linear Search

Best Case : O(1)

Just imagine that we are lucky. And the element we are trying to find is in the first location in the array.

So, we don't have to traverse any element and find the element at the very first location.

Average case : O(n)

Worst Case : O(n)

Just think ! What if the element resides at the last location in the array.

We have to traverse all the elements to reach the end of the array. And if there are 'n' elements in the array. Running time would be O(n).

❮❮ PREV NEXT ❯❯