ADJACENCY LIST DATA STRUCTURE

Adjacency List Data Structure is another implementation of Graph, that is quite easy to understand.

As the name suggests, in 'Adjacency List' we take each vertex and find the vertices adjacent to it(Vertices connected by an edge are Adjacent Vertices).

Then construct a Linked List from each vertex.

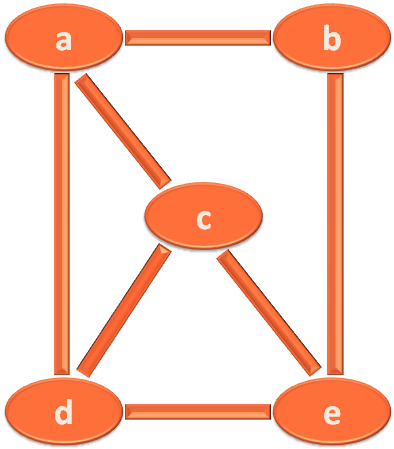
Let's understand with the below example :

Now, we will take each vertex and index it.

i.e.

a - 0
b - 1
c - 2
d - 3
e - 4

Note : While coding, the above representation of indexing comes handy.

At first we take the vertex 'a'. And try finding the vertices adjacent to it.

And find, vertices 'b', 'c' and 'd' are adjacent to it.

So, for vertex 'a' at index '0', we construct a LinkedList with elements, 'b', 'c' and 'd'.
Similarly, we take the vertex 'b' at index '1'. And try finding the vertices adjacent to it.

And find, vertices 'a' and 'e' are adjacent to it.

So, for vertex 'b', we construct a LinkedList with elements, 'a' and 'e'.
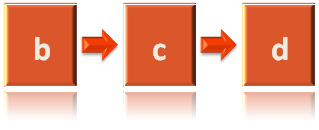
Then, we take vertex 'c' at index '2' and construct a LinkedList with elements, 'a', 'd' and 'e'.
Next, we deal with vertex 'd' at index '3' and construct a LinkedList with elements, 'a','c' and 'e'.
And lastly, we take with vertex 'e' at index '4' and construct a LinkedList with elements,'b', 'c' and 'd'.

So, we are keeping a track of the Adjacency List of each Vertex.

What would be the space needed for Adjacency List Data structure ?

If we suppose there are 'n' vertices. So, for storing vertices we need O(n) space.

And the length of the Linked List at each vertex would be, the degree of that vertex.

As for example, if you consider vertex 'b'. It has degree 2. And there are 2 adjacent vertices to it.

So, the sum of degrees would be 2*n.

Now, if we consider 'm' to be the length of the Linked List.

The total space required : O(n+m)

Note : The Adjacency List Data Structure is the standard and most preferred way of representing Graphs.

❮❮ PREV NEXT ❯❯