Adjacency Matrix Data Structure is another implementation fo Graph that is the most easy data structure to understand.
Let's understand with the below undirected graph :
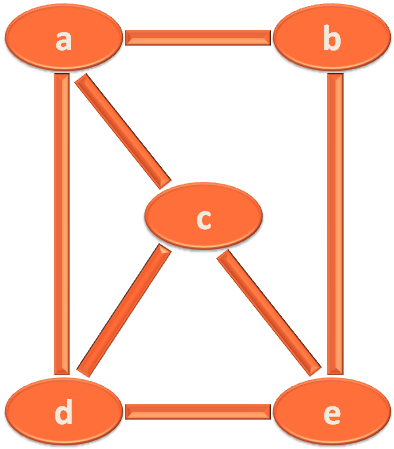
Let us suppose, there are 5 vertices. a, b, c, d and e.
Now, there is an edge between 'a' and 'b' or 'b' and 'a'. i.e. (a,b) or (b,a).
Similarly, there are other edges like (a,c) or (c,a), (c,e) or (e,c), (e,b) or (b,e), (e,d) or (d,e), (d,c) or (c,d) and (d,a) or (a,d).
Now, we will see an elegant solution to represent the edges.

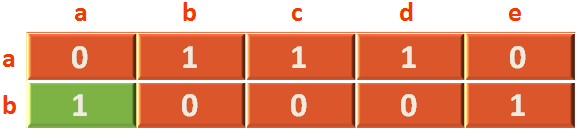
If you look at the extreme left, you can find, each row is represented by a vertex (i.e. a, b, c, d and e).
Again, if you have a look at the top. Each column is also represented by a vertex (i.e. a, b, c, d and e).
Now, if you look at the intersection of a row and column. You can find the number '1' represents an edge and number '0' represents there is no edge.
Say for example, we know that there is an edge between a and b or b and a.
So, if we look at the intersection of a and b. We can find the number '1' in it.

Similarly, if we see the intersection of b and a. We can also find the number '1' in it.
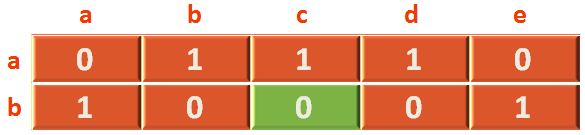
Now, we know that there is no edge between b and c. So, if you check the intersection, you can find number '0' in it.
Now, just pause! Think for a moment!
Can the above structure in the form of a 2D array?
Yes, off course we can.
For our convenience, let us represent the vertices in the form of numbers.
Say,
So, let us change the graph in the same form.
What I meant was instead of a, b, c, d and e. Let us represent it as 0, 1, 2, 3 and 4.
And the graph becomes :
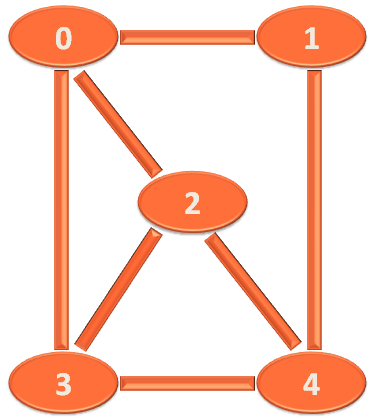
And the below Adjacency Matrix becomes :
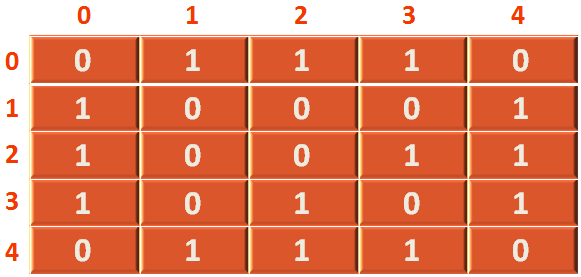
Now, can we represent the above as a 2d array?
If the name of the array is 'arr'. Then arr[0,1] has the number 1. That represents an edge between.
Similarly, there is an edge between vertex 0 and 3. And arr[0,3] has the number 1 in it.
Just think for a moment. Although there is just 1 edge in a graph, still you have to construct a 2D array as mentioned above.
As the edge that is present will be represent by the number '1' and the even though there is no edge. We still have to represent it with number '0'.
Space needed for Adjacency Matrix Data Structure : O(n)
To remove an edge just go to that edge and set it to '0'.
Time needed for Adjacency Matrix Data Structure to search or remove an edge : O(1)