SELECTION SORT

Selection Sort is also one of the simplest algorithm where we try finding the highest or lowest element and place it at the correct position.

Let us understand this with the below example.

Let us say we have 5 numbers in random order and we have to sort them in ascending order.

Now, let us apply Selection sort algorithm to sort the numbers and at every pass we will move from 1st location to 5th location and try finding the largest element and place the largest element at the end of the list.

Initially we will assume that the maximum value is at the first location(Name it as CurrentMaximum) and keep on comparing it with the other values. When we find a value that is greater than CurrentMaximum, we will make the 'CurrentMaximum' point to that. Sounds tough? Let us simplify.

Let us make the 'CurrentMaximum' point to the 1st location.

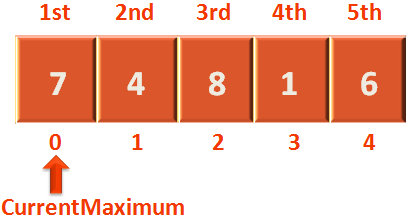
Then, check if the 'CurrentMaximum' i.e. 7 is less than the number in 2nd location i.e. 4. In this case 7 is greater than 4. So, 'CurrentMaximum' remains at 7 in the first iteration.

In 2nd Iteration, we compare 'CurrentMaximum' i.e. 7 with the element in 3rd location i.e. 8. And find 7 is less than 8.

Now, we make the 'CurrentMaximum' point to the 3rd location.

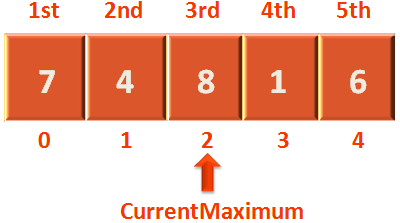
So, the 'CurrentMaximum' points to 8 now.

In the 3rd iteration, we compare 'CurrentMaximum' i.e. 8 with the element in the 4th location i.e. 1 and find 8 is greater than 1. So, the 'CurrentMaximum' points at 8.

In the 4th iteration, we compare 'CurrentMaximum' i.e. 8 with the element in the 5th location i.e. 6 and find 8 is greater than 6. So, the 'CurrentMaximum' points at 8.

Now, that we have come to the end of the list. It is time to swap the 'CurrentMaximum' i.e. 8 with the element in the 5th location i.e. 6.

So, at the end of 1st pass 8 is swapped with 6 and the list becomes:

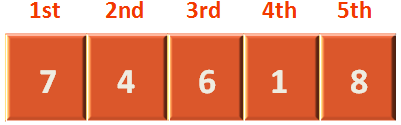
So, the highest value 8 is placed at the end of the list and 8 is considered to be sorted.

In the second pass we will consider running the algorithm between 1st to 4th location as the element in the 5th location is already sorted.

Just like in pass 1, we will point 'CurrentMaximum' to the 1st location.

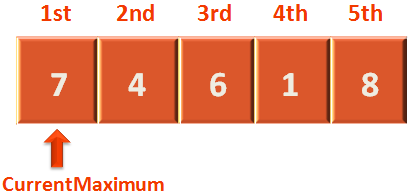
Check if the 'CurrentMaximum' i.e. 7 is less than the number in 2nd location i.e. 4. In this case 7 is greater than 4. So, 'CurrentMaximum' remains at 7 in the first iteration.

In 2nd Iteration, we compare 'CurrentMaximum' i.e. 7 with the element in 3rd location i.e. 6. And find 7 is greater than 6. So, 'CurrentMaximum' remains at 7 in the second iteration as well.

In the 3rd iteration, we compare 'CurrentMaximum' i.e. 7 with the element in the 4th location i.e. 1 and find 7 is greater than 1. So, the 'CurrentMaximum' points at 7.

Now, that we have come to the end of the list (Since, the element in 5th location i.e. 8 is already sorted). It is time to swap the 'CurrentMaximum' i.e. 7 with the element in the 4th location i.e. 1.

So, at the end of 2nd pass 7 is swapped with 1 and the list becomes:

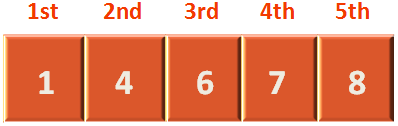
So, the second highest value 7 is placed at the 4th location and the elements in 4th and 5th location i.e. 7 and 8 is considered to be sorted.

Similarly, in the third pass we will consider running the algorithm between 1st to 3rd location as the elements in 4th and 5th location is already sorted.

Just like in pass 1 and 2, we will point 'CurrentMaximum' to the 1st location.

Check if the 'CurrentMaximum' i.e. 1 is less than the number in 2nd location i.e. 4.

In this case 1 is less than 4. So, 'CurrentMaximum' points to the 2nd location i.e. at 4.

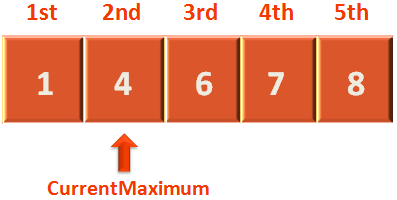
In 2nd Iteration, we compare 'CurrentMaximum' i.e. 4 with the element in 3rd location i.e. 6. And find 4 is less than 6.

So, 'CurrentMaximum' points to the 3rd location i.e. at 6.

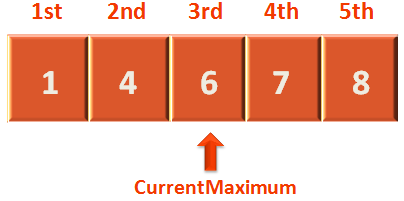
Now, that we have come to the end of the list (Since, the elements in 4th and 5th location i.e. 7 and 8 is already sorted). It is time to compare the 'CurrentMaximum' i.e. 6 with the element in 3rd location.

And guess what the 'CurrentMaximum' is pointing to the 3rd location currently. Which means the element in the 3rd location i.e. 6 is already sorted.

So, at the end of 3rd pass the list becomes:

So, the third highest value 6 is placed at the 3rd location and the elements in 3rd, 4th and 5th location i.e. 6, 7 and 8 is considered to be sorted.

In the 4th pass we will consider running the algorithm between 1st and 2nd location as the elements in 3rd, 4th and 5th location are already sorted.

Just like in pass 2 and 3, we will point 'CurrentMaximum' to the 1st location.

Check if the 'CurrentMaximum' i.e. 1 is less than the number in 2nd location i.e. 4.

In this case 1 is less than 4. So, 'CurrentMaximum' points to the 2nd location i.e. at 4.

Now, that we have come to the end of the list (Since, the elements in 3rd, 4th and 5th location i.e. 6, 7 and 8 is already sorted). It is time to compare the 'CurrentMaximum' i.e. 4 with the element in 2nd location.

And we found the 'CurrentMaximum' is pointing to the 3rd location currently. Which means the element in the 2nd location i.e. 6 is already sorted.

So, at the end of 4th pass the list becomes:

So, the fourth highest value 4 is placed at the 2nd location and the elements in 3rd, 4th and 5th location i.e. 6, 7 and 8 is considered to be sorted.

So, finally the list is considered to be Sorted.