TREE TRAVERSAL

We have already looked at the Binary Tree. Now, there should be a way to visit the Nodes of the Tree.

And Yes ! Visiting all the Nodes of the Tree in a specific order is 'Tree Traversal'.

There are three ways of visiting the Nodes of the Tree :

Now, let us take the below Tree and understand how all the three ways of Tree Traversal works.

So, Preorder Tree Traversal is,

So, we would visit the Root element first, then visit all the elements of the Left Sub-Tree and finally, visit all the elements of the Right Sub-Tree.

Now, the Root element is Node 'A'.

The Right Sub-Tree is,

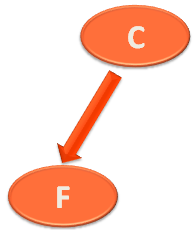
And the Left Sub-Tree is,

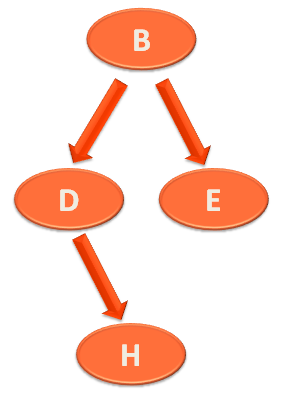
So, the first thing we will do is, print the root element(i.e. 'A') first. As the Preorder Traversal is 'Root --> Left --> Right'.

Then we come to the Left Sub-Tree as per the Preorder Traversal process. And if you look at the Left Sub-Tree,

'B' is the root of the Left Sub-Tree. So, we print 'B' next,

Then we come to the left Sub-Tree of 'B'.

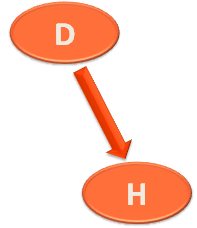
And find 'D' is the root of the left Sub-Tree of 'B'. So, we print 'D'.

Then we try finding the left Sub-Tree of 'D'. But 'D' doesn't have any Left Sub-Tree. So, as per the traversal process 'Root --> Left --> Right', we will go to the Right Sub-Tree of 'D'. And find 'H' there.

So, we print 'H'.

Now, we find that 'H' doesn't have any child.

So, we travel up, and go to 'B'.

And we find that the left Sub-Tree of 'B' is already visited.

So, as per the traversal process 'Root --> Left --> Right', we will go to the Right Sub-Tree of 'B'. And find 'E' there.

So, we print 'E'.

Again we travel up and reach 'A'.

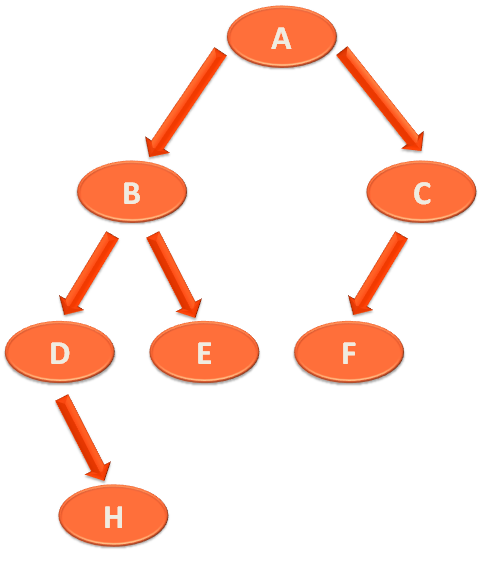
And we find that the Left Sub-Tree of 'A' is already visited. So, we visit the Right Sub-Tree of 'A'.

And find that 'C' is the root of the Right Sub-Tree.

So, we print 'C'.

And, as per the traversal process 'Root --> Left --> Right', we will go to the Left Sub-Tree of 'C'. And find 'F' there.

So, we print 'F'.

Then search for the Right Sub-Tree of 'C'. But we find it's empty.

And thus, all the Nodes of the Tree are visited and we complete the Pre-Order traversal with this.

And the final result for re-Order traversal is,

Next, let us see the Postorder traversal for the same tree.

So, Postorder Tree Traversal is,

So, we would visit all the elements of the Left Sub-Tree element first, then visit all the elements of the Right Sub-Tree and finally, visit the Root element.

Now, the Root element is Node 'A'.

And, as per the Postorder Traversal, 'Left --> Right --> Root'. We will visit the Left Sub-Tree.

And the Left Sub-Tree is,

Now, 'B' is the root of the Left Sub-Tree. And, as per the Postorder Traversal, 'Left --> Right --> Root'. We will visit the Left Sub-Tree of 'B'.

The Left Sub-Tree of 'B' is,

So, 'D' is the root of the Left Sub-Tree of 'B'. And, as per the Postorder Traversal, 'Left --> Right --> Root', we are supposed to visit the Left child of 'D'. But 'D' doesn't have any Left Child.

So, we visit the Right child of 'D'. Which is 'H'.

And we print 'H' first.

And since we have printed the Right element (i.e. H). Next, we print the root element (i.e. D) following the order 'Left --> Right --> Root'.

So, we print 'D'.

Now, we are done with the Left Sub-Tree of 'B',

So, it is time for us to travel upwards and reach 'B'.

Now, as per the Postorder Traversal, 'Left --> Right --> Root'. The Left Sub-Tree of 'B' is already visited. Now, it us time to go to the right element.

And find 'E' is the right element of 'B'.

And since, 'E' has no children. We print 'E' next.

Now, we are done with the right element of 'B'. So, we print 'B' next(As 'B'is the root).

So, we are done with all the left Sub-Tree of 'A'.

Now, it is time to deal with the right Sub-Tree of 'A'.

And the Right Sub-Tree of 'A' is,

So, 'C' is the root of the Right Sub-Tree of 'A'.

And, as per the Postorder Traversal, 'Left --> Right --> Root'. We come to the left element of 'C'. And find 'F' there.

So, we print 'F'.

Then try finding the right element of 'C'. But 'C' has no right child.

So, we print the root element i.e. 'C'.

And we are done with the right Sub-Tree of 'A'.

And since, we are done with the Left Subtree and Right Sub-Tree of 'A'. It's time to print 'A' and stop the execution.

Next, let us see the Inorder traversal for the same tree.

So, Inorder Tree Traversal is,

So, we would visit all the elements of the Left Sub-Tree element first, then visit the Root element and finally, visit all the elements of the Right Sub-Tree .

Now, the Root element is Node 'A'.

And, as per the Inorder Traversal, 'Left --> Root --> Right'. We will visit the Left Sub-Tree.

And the Left Sub-Tree is,

Now, 'B' is the root of the Left Sub-Tree. And, as per the Inorder Traversal, 'Left --> Root --> Right'. We will visit the Left Sub-Tree of 'B'.

The Left Sub-Tree of 'B' is,

So, 'D' is the root of the Left Sub-Tree of 'B'. And, as per the Inorder Traversal, 'Left --> Root --> Right', we are supposed to visit the Left child of 'D'. But 'D' doesn't have any Left Child.

So, we visit the root element i.e. 'D'.

And we print 'D' first.

And since, we have printed the Root element (i.e. D). Next, we print the Right element (i.e. H) following the order'Left --> Root --> Right'.

So, we print 'H'.

Now, we are done with the Left Sub-Tree of 'B',

So, it is time for us to travel upwards and reach 'B'.

Now, as per the Postorder Traversal, 'Left --> Root --> Right'. The Left Sub-Tree of 'B' is already visited. Now, it us time to print the Root element i.e. B.

Now, we are done with the root element i.e. 'B'. So, we print 'E' next(As 'E' is the only element in the right side of 'B').

So, we are done with all the left Sub-Tree of 'A'.

Now, it is time to print 'A'.

Now, it is time to deal with the Right Sub-Tree of 'A'.

And the right Sub-Tree of 'A' is,

So, 'C' is the root of the Right Sub-Tree of 'A'.

And, as per the Inorder Traversal, 'Left --> Root --> Right'. We come to the left element of 'C'. And find 'F' there.

So, we print 'F'.

Then we print the root element i.e. 'C'.

And we are done with the Inorder traversal of the above tree.