QUICK SORT

Quick Sort is an efficient algorithm that also works on Divide and Conquer strategy like Merge Sort. The benefit of Quick Sort over Merge Sort is, Quick Sort does the sorting 'in place'. i.e. No additional array will be needed to store the values while performing Quick Sort.

As said, Quick Sort works on Divide and Conquer strategy. Just think that in Quick Sort, we will take an array and divide it into two parts. And name those two parts as Higher part and lower part. Such that, the higher part will contain all the elements those are greater than the elements in lower part.

Similarly, the lower part will contain all the elements those are less than the elements in the higher part.

Say for example:

We have the below array,

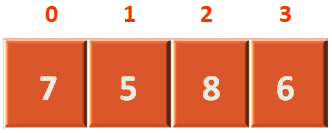
Now, we divide the list into two parts. Such that the Lower Part has all the elements that are lower than the elements in the higher part and vice versa.

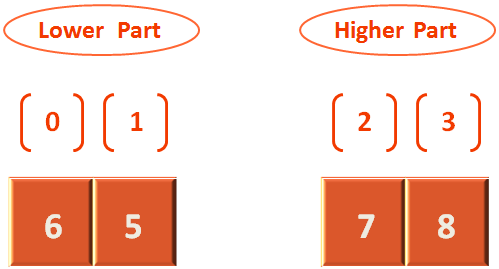
The Higher Part contains 7 and 8. Which is greater than the elements in lower part i.e. 6 and 5.

Now, the easiest part is, if we sort the higher part and lower part separately. And combine them, we get a sorted array.

Why?

The Lower part has all the smaller elements in it i.e. 6 and 5. And the higher part has all the larger elements.

Now, if we sort both Higher Part and Lower Part separately.

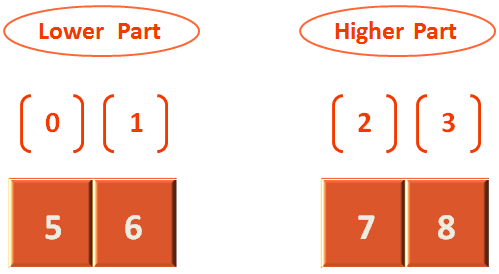
And, merge the Lower Part and Higher Part, we get a sorted array.

Just remember that its a three step process :

Now, the million dollar question is,

The Partitioning of Lower and Higher Part is done based on an element called the 'Pivot element'.

By the definition of english dictionary, Pivot is a fixed point supporting something that turns.

And the same definition applies here.

We choose an element from the Array and make it the pivot element. All the elements that are less than the pivot element sits on the Lower Part and the elements greater than or equal to the pivot element sits on the higher part. Quite simple! Right?

Now, let's see the actual implementation.

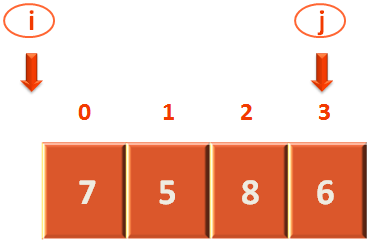
Let us consider the below array arr[4],

Usually, we can select any element to be the pivot element. And in this case, let us select the first element to be the Pivot element. And the first element is arr[0].

So, the pivot element is 7.

Now, if we compare all the elements with the pivot element (i.e. 7) and those elements which are less than the pivot element (i.e. 7) will be placed on the Left side or Lower part.

And, all the elements that are greater than or equal to the pivot element (i.e. 7) , will be placed on the Right side/Higher Part.

Now, we will run two pointers, 'i' and 'j'. Where 'i' will start from a location just before the first position and 'j' will start from the a location just after the last position.

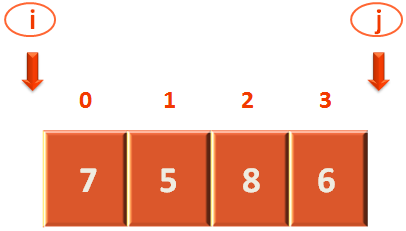
So, the idea is:

Sounds quite theoretical ! Right ?

Let us see the implementation below:

In the 1st step, the first thing we will do is, move 'j' to the left. i.e. Make 'j' point to the last element, then check if the last element (i.e. Where 'j' is currently pointing) is less than or equal to the pivot element or not.

In this case the last element is '6', that is less than the pivot element i.e. 7.

So, the 'j' element is ready to be swapped.

Now, it's time to deal with 'i'. So, in this step itself, we will make 'i' point to the 1st element

And check if the 1st element(i.e. Where 'i' is currently pointing to) is greater than or equal to the pivot element or not.

In this case the 1st element is '7', that is equal to the pivot element i.e. 7.

Now, the 'i' element is also ready to be swapped.

Now since, both the 'i' and 'j' elements are ready to be swapped. We can swap the element in the 1st position i.e. '7' with the element in the last position i.e. 6.

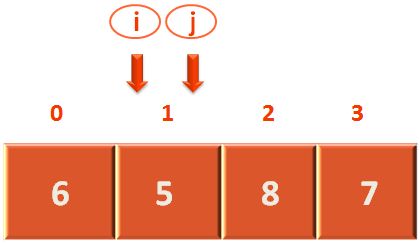
And the list after swapping becomes,

In the 2nd step, the first thing we will do is, make 'j' point to the 2nd last location

And check if the 2nd last element(i.e. Where 'j' is currently pointing to) is less than or equal to the pivot element or not.

And in this case the 2nd last element is '8' which is not less than or equal to the pivot element i.e. 7.

And since, our idea is to find a number that is less than or equal to the pivot element. So, we make 'j' point to the third last location.

And we can see that, there is 5 in that location( i.e. Where 'j' is currently pointing to). So, we check if 5 is less than the pivot element ( i.e. 6) or not.

And we find that 5 is less than the pivot element.

So, we mark the 'j' element for swapping.

Now, the time is to deal with 'i'.

So, firstly we will make 'i' point to the 2nd location,

And check if the 2nd element(i.e. Where 'i' is also currently pointing to) is greater than or equal to the pivot element or not.

And in this case, the 2nd element is '5' that is less than the pivot element i.e. 7.

So, we make 'i' point to the 3rd location.

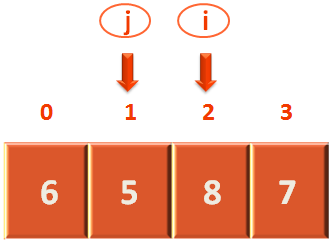
And check that if the 3rd element(i.e. Where 'i' is also currently pointing to) is greater than or equal to the pivot element or not.

And find that the 3rd element is '7' which is equal to the pivot element i.e. 7.

So, 'i' element is marked for swapping.

BUT ! Just Wait. Isn't this is the place where 'i' and 'j' have crossed each other. So, we don't have to swap 'i' and 'j' element.

And it's time for us to stop and note the point where 'j' is currently pointing to.

Now, just look closely. The list is already divided into two parts. All the elements that are less than the pivot element i.e. 7 are on the left side or lower part and all the elements greater than or equal to the pivot element i.e. 7 are on the right side or the higher part.

But hang on ! This is not the end. We have to keep on subdividing each part until there is only one element left.

So, what we will do is, take the Lower and Higher part separately and sub-divide each part into Lower and Higher part.

Let's simplify it.

Let's take the above Lower part first and reset the pointers. 'i' to a location just before the 1st element and j to a location just after the last location(As we have done above).

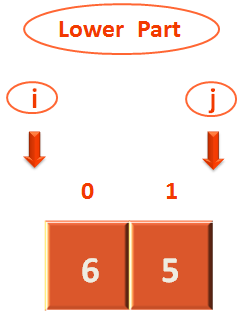
Next, we will have to take the pivot element. Which should be the first element. And in this case the first element is 6.

So, the pivot element is 6.

And, as we have done earlier, we will compare all the elements with the pivot element and those elements which are less than the pivot element will be placed on the Left side or Lower part.

And, all the elements that are greater than or equal to the pivot element, will be placed on the Right side/Higher Part.

So, at first we will make 'j' point to the last location,

And check if the last element (i.e. Where 'j' is currently pointing to) is less than or equal to the pivot element or not.

In this case the last element is '5' , that is less than the pivot element i.e. 6.

So, 'j' element is ready to be swapped.

Now, let us deal with 'i' . As usual the first thing we will do is make 'i' point to the 1st location.

we will check if the 1st element(i.e. Where 'i' is currently pointing to) is greater than the pivot element or not. In this case the 1st element is '6' , that is equal to the pivot element i.e. 6.

Now, the 'i' element is also ready to be swapped.

So, we can swap the element in the 1st position i.e. '6' with the element in the last position i.e. 5.

And the list after swapping becomes,

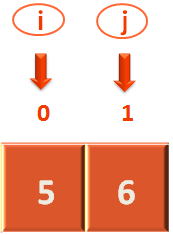
Now since, 'i' and 'j' have not crossed each other or have overlapped, we have to continue with the 2nd Step.

Now, the first thing we will do is make 'j' point to the 1st location.

Then check if the first element (i.e. Where 'j' is currently pointing to) is less than or equal to the pivot element or not.

In this case the first element is '5', that is less than the pivot element i.e. 6.

So, we mark 'j' element for swapping.

Now, let us deal with 'i'. As usual the first thing we will do is make 'i' point to the 2nd location.

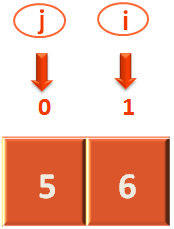
we will check if the 2nd element(i.e. Where 'i' is currently pointing to) is greater than or equal to the pivot element or not. In this case the 2nd element is '6', that is greater than the pivot element i.e. 5.

So, the 'i' element is also ready to be swapped.

BUT! Just wait. 'i' and 'j' has just crossed each other.

So, it's time for us to STOP and note the position where 'j' is pointing to.

And Bingo ! the list is already divided into two parts. All the elements that are less than the pivot element i.e. 6 are on the left side and all the elements greater than or equal to the pivot element 6 are on the right side.

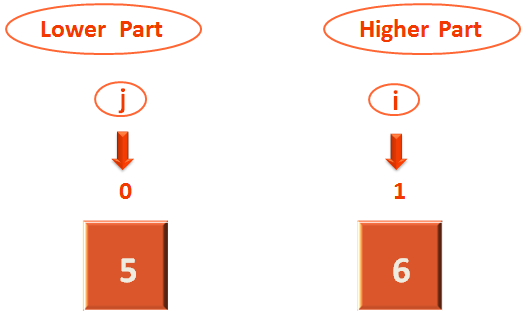
And no further division is needed as each part consists of one element each.

Now, let us take the higher element from above, consisting two elements.

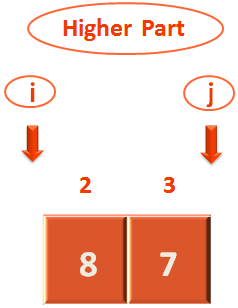
Similarly, let's take the pivot element from the first location, which is 8 in this case.

Now, as per the rule. Let us make 'j' point to the last location of Higher Part.

And, we will check the element where 'j' is currently pointing to (i.e. 7) is less than or equal to the pivot element or not.

And the element where 'j' is currently pointing to (i.e. 7) is less than the pivot element i.e. 8.

So, we can mark the 'j' element for swapping.

Now, it is the time to deal with 'i'.

So, at first we need to make 'i' point to the 1st element.

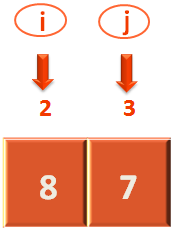
Now, we will check if the 1st element(i.e. Where 'i' is currently pointing to) is greater than or equal to the pivot element or not. In this case the 1st element is '8', which is equal to the pivot element i.e. 8.

So, 'j' element is also marked for swapping.

So, we swap the values of 'i' and 'j'.

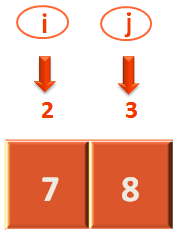
Now since, 'i' and 'j' have not crossed each other or have overlapped, we have to continue with the 2nd Step.

Now, the first thing we will do is make 'j' point to the 1st location.

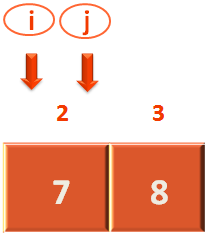
Then check if the first element (i.e. Where 'j' is currently pointing to) is less than or equal to the pivot element or not.

In this case the first element is '7', that is less than the pivot element i.e. 8.

So, we mark 'j' element for swapping.

Now, let us deal with 'i'. As usual the first thing we will do is make 'i' point to the 2nd location.

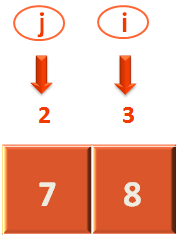
we will check if the 2nd element(i.e. Where 'i' is currently pointing to) is greater than or equal to the pivot element or not. In this case the 2nd element is '8', that is equal to the pivot element i.e. 8.

So, the 'i' element is also ready to be swapped.

BUT ! Just wait. 'i' and 'j' has just crossed each other.

So, it's time for us to STOP and note the position where 'j' is pointing to.

And Yay ! the list is already divided into two parts. All the elements that are less than the pivot element i.e. 8 are on the left side and all the elements greater than or equal to the pivot element 8 are on the right side.

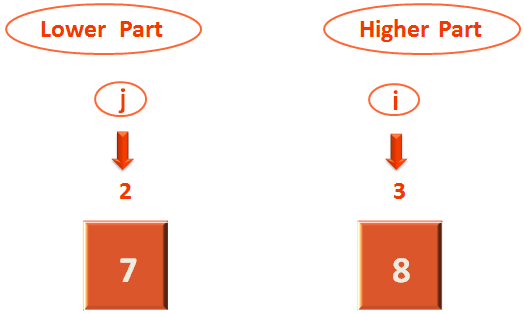
And no further division is needed as each part consists of one element each.

And, finally it's time to club all the lists.

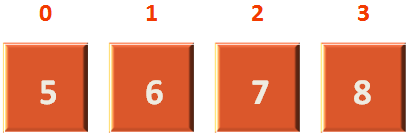
Into one final list.

And we get a sorted list/array.