GRAPH

A Graph is composed of a set of 'Vertices' and a set of 'Edges'.

Let us understand 'Vertices' and 'Edges' with the below example :

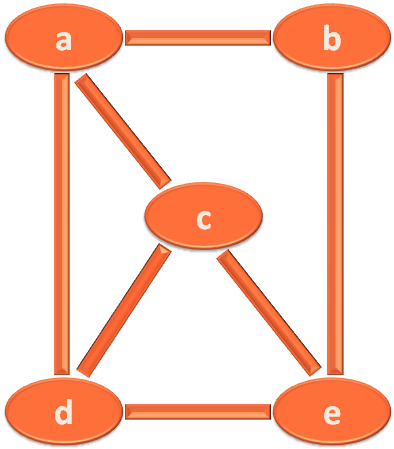
In the above diagram, a, b, c, d and e are the 'vertices'. And the lines connecting them are the 'edges'.

Just consider, you are a bus driver. And a,b,c,d and e are destinations and the lines connecting them are the roads.

An 'edge' is a pair of vertices.

So, the 'edge' that is connecting vertices 'a' and 'b' can be represented as,

Similarly,

The 'edge' connecting 'c' and 'e' is represented as,

There are two types of Graphs :

The Graph we have seen above is an undirected graph. Where no direction is specified.

And in a directed graph, direction would be specified.

If we modify the above graph to a directed graph :

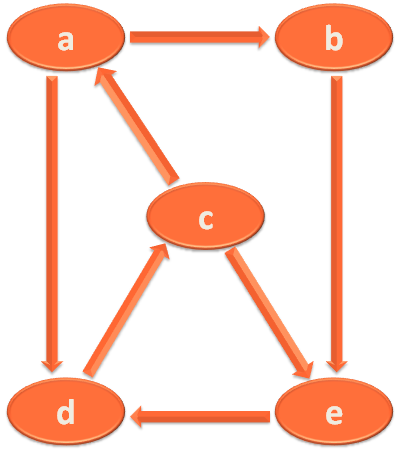
In the above graph, the direction is specified.

Where a,b is an edge, but b,a cannot be represented as an edge. Guess why? As the direction is specified.

Let us take the undirected graph to explain the graph terminologies.

Vertices connected by an edge are Adjacent Vertices.

(a,e) is not an adjacent vertices but (a,c) can be called adjacent vertices, as it is connected by an edge.

A degree of vertex is the number of adjacent vertices it has.

The degree of vertex 'a' is 3 as it has 3 adjacent vertices i.e. (a,b) (a,c) and (a,d).

Let us take the above example to explain this.

You are a bus driver and a, b, c, d, e are bus stops. And the edges are the roads.

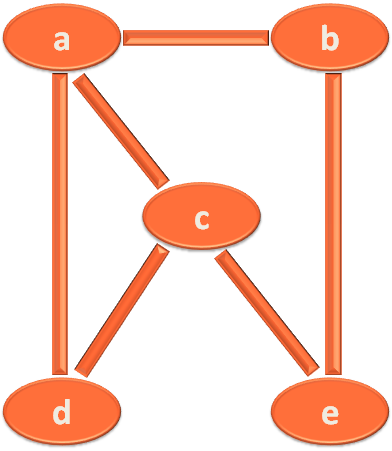
Now, if you are asked to travel from a to c. How would you do it?

You could have taken the path a to c or ( a,c).

Or to drop passengers to location b and c. You might have taken the path ( a,b,e,c). And so on.

And the same logic applies here. ( a,c), ( a,b,e,c) is a path but ( a,b,c) is not a path as there is no edge connecting b and c.

If there is a path between two vertices, they are said to be connected.

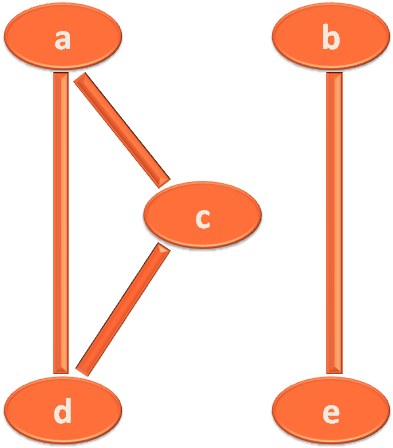
There is no path from a, c, d and b,e.

A Tree in a Graph is connected graph without cycles.

Let us understand with an example :

The below graph is not a Tree. Guess why ?

The below graph is not a Tree because it is forming a cycle. i.e. a,c,d,a.

Now, if we remove the edge (a,d).

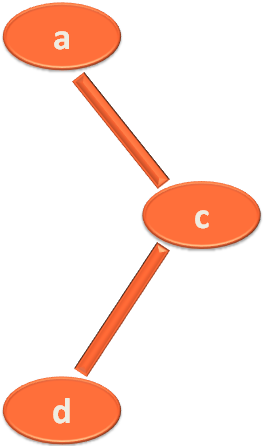
It becomes are tree as it is not forming a cycle anymore.

Forest is a collection of Trees.

It is a Graph in which there is a edge between every pair of vertices.

The above graph is a Complete Graph as there is not a single edge that is missing. In other words, you cannot draw anymore edges connecting two vertices.

In the above case we have 5 Vertices.

Let us suppose, 'n' be the number of vertices.

Then we can write,

Number of edges in a complete graph = n(n-1)/2

Now, if we consider the above example and substitute the value n with number of vertices,

Number of edges in a complete graph = 5(5-1)/2

                   = 10

Now, to cross verify, if we count the number of edges in the above graph. We can see it's 10.

Spanning tree as the name suggests is a tree that is derived from an existing graph.

Let us say, in the below graph, the vertices are the number of cities. And the edges are the roads connecting them.

Now, let's say, we want to cut of the extra roads connecting the cities. i.e. If we want to reach city 'c'. We can take the path (a,c) or (a,d,c) or (a,d,e,c) and so on.

We don't want that. We just need a single road that goes from a to c.

And thus comes spanning tree.

Let us take the below graph,

If we want to make a spanning tree out of the above graph. We need to convert it to a tree and make sure that all the vertices are present.

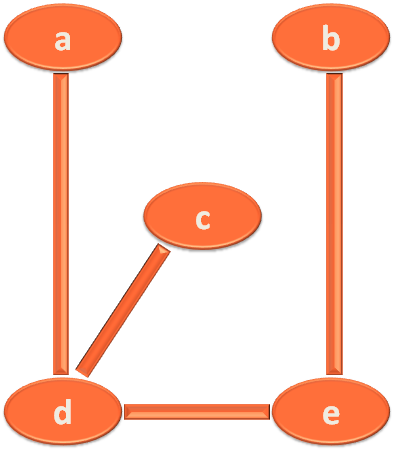
Fair enough !

Now, it is a spanning tree derived from the above graph.