

As we have already seen, the name Spanning Tree is comprised of the terms 'Spanning' and 'Tree'.
And as we know, a 'Tree' is a connected sub-graph with 'no cycles'.
And 'Spanning' says, you have to include all the vertices of a graph.
And if you combine Spanning and Tree, it is a sub-graph that includes all the vertices of the Graph, which has no cycles.
Let us take the below graph as an example,
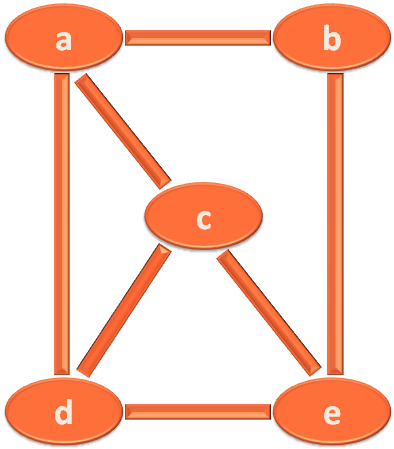
If we want to make a spanning tree out of the above graph. We need to convert it to a tree and make sure that all the vertices are present.
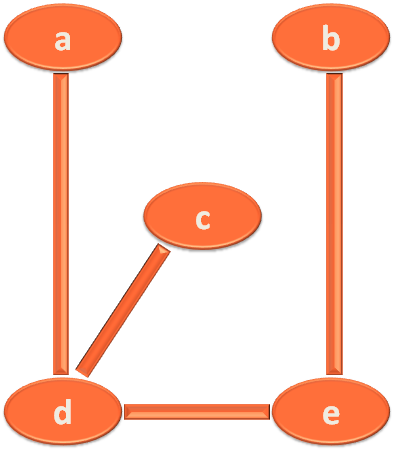
Fair enough !
Now, it is a spanning tree derived from the above graph.
A Minimum Spanning Tree is a spanning tree with minimum length or weight.
Now, what is minimum length or weight?
The minimum length or weight is the minimum length of the edges. i.e. Every edge should have a length. And we need to construct a spanning tree, only with those edges that are smallest in length.
Hard to understand ?
Let us simplify with the below example.
We will be rewriting the above graph, by giving length for every edge.
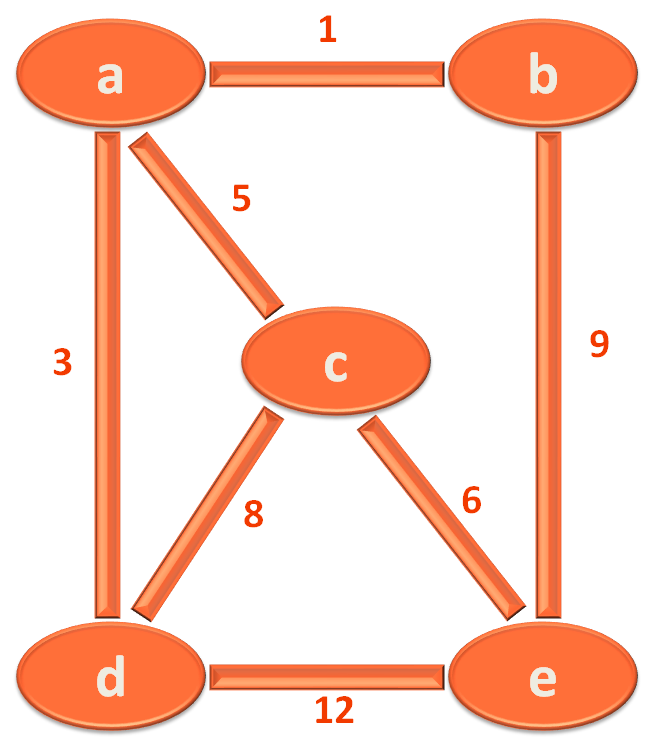
Let us see the edge and its corresponding length.

Now, let us take the edges with smallest length/weight and try forming a Spanning Tree.
So, we can take the edges (a,b), (a,d), (a,c) and (c,e). And form a spanning tree which would be a minimum spanning tree.

What we have done is, started from the edge of smallest length. i.e. The edge a,b has the smallest edge of length 1.
Next, we searched for the edge with second minimum length. i.e. The edge a,d has the edge length(i.e. 3) that is smaller than all the other edges but greater than edge a,b.
Similarly, we have taken all the edges in the similar fashion. And the above minimum spanning tree is formed.
Also, if you take the sum of all the edges of the minimum spanning tree,
The total length becomes 15. Which is the smallest sum compared to the sum of other edges.
The answer is, we haven't seen the 'How' part.
There are efficient algorithms :
That we will be seeing in the next tutorial.