Logarithm ! The term itself is quite scary ! Isn't it ?
But trust me, it isn't. We will make it super simple for you to understand.
While performing complexity analysis, the term 'log' or 'logarithm' is quite commonly used.
We have often seen log2n. But how is it calculated? And how is it said to be so effective?
Let us see below,
The condition (Again ! Don't get scared by the below condition),
Is true, if and only if,
Just remember 'b' in the above expression is called base. We might not write it often because in complexity analysis, the base is often 2. i.e. log2n.
So, from Computer Science or Algorithm perspective, the base is always 2.
And the above condition got simplified.
i.e.
Is true, if and only if,
Now, say the value of 'n' is 4. So, let's substitute the value of log2n with log24 and 2m = n with 2m = 4.
All we have done is, substituted the value of 'n' with 4.
So the condition,
Is true, if and only if,
And we know that,
So, we can say that m = 2 in this case.
And if we substitute the value of m with 2.
The expression,
becomes
In other words the value of log 4 is 2.
Fair enough !
Now, let us take another example,
Say, you are asked to calculate the value of 'log 16'.
Now, you would go to the expression,
And since you are asked to calculate the value of 'log 16', the value of 'n' is 16. So, we will substitute 'n' with 16.
Now, 2 to the power what is equal to 16? In other words, how many time 2 needs to be multiplied to itself to get 16.
2 needs to be multiplied 4 times with itself to get 16.
So, the value of 'm' is 4.
And the value of log 16 is 4.
We have already seen 'log n' or 'log 16' is equal to 4.
Now, say if we double the value of 'n' in 'log n'. i.e. We double the value of 16 in log 16.
So, it is 'log 32'.
Now, if we calculate 'log 32'. We need to go to the expression,
Substitute the value of 'n' with 32.
So, 2 to the power what is 32 ? It is 5. 2 to the power 5 is 32.
So, 'log 32' is 5.
Just have a closer look.
'log 16' is equal to 4. Now, we have doubled the value of n, i.e. 'log 32'. And the value of 'log 32' is 5.
The 'n' of 'log n' had increased from 16 to 32 and the value of 'log 16' was 4 and 'log 32' is 5.
Which means, even though 'n' of 'log n' doubles(i.e. From 16 to 32). But its value only increases by 1(i.e. From 4 to 5).
Now, if you compare this with Complexity Analysis. Just imagine O(n) or O(32) is quite larger than O(log n) or O(log 32). As the value of 'log 32' is just 5.
Let us clear it with the below example,
Say, we have an array that has 16 elements in it.

Now, say you are asked to search '16' from the array. And since the element is in the last location. You have to iterate 16 times to search for the number 16. i.e. You would start searching the first element then the second element then the third and continue 16 times until you find 16.
for(int i = 0 ; i < 16 ; i++) {
if(arr[i] == 16) {
System.out.println("The element 16 is found");
}
}Now, let's imagine you have found a better way to search the number. i.e. At every iterationyou divide the array into two halfs and search the element.
So, in the first iteration, we have divided the array into two parts,

And ignore the first part. And we have the second part with us.

Then in the second iteration, we further divide above half into two parts.

And take the second part.

Again in the third iteration, we divide the array into two parts.

And take the second part.
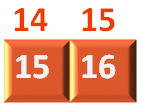
Then in the fourth iteration, we divide the array into two parts.

And take the second part.

And find the element 16 in just 4 iterations.
Justy recall ! To find the same element, you had to run your loop 16 times. But with this new logic, you just have to run your loop 4 times to search the same element out of 16 elements.
Which is 'log n'. Or, 'log 16' i.e. 4.
To make it more simple. There are '16' elements in the array. And to search an element from the array we had to iterate just 4 times.
Or in other words 'log 16' times. As 'log 16' is 4.