BFS-BREADTH FIRST SEARCH

BFS - Breadth First Search is one of the Graph traversal algorithm that is quite easy to understand.

Let us understand with the below example :

Say, you are a courier delivery guy and there are 5 cities (a, b, c, d and e) where you have to deliver the courier packages.

But your Boss is very strict and he doesn't want you to visit the same city twice.

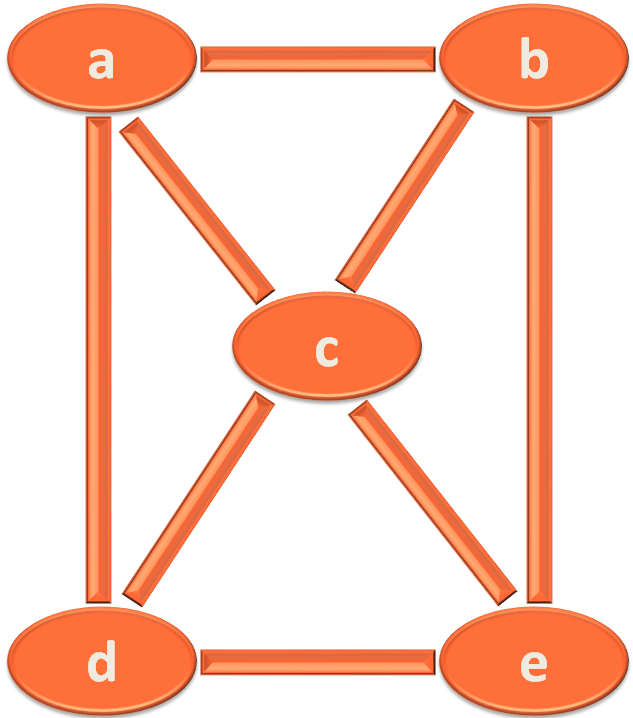
Below is the undirected Graph, which is also a roadmap that your Boss has given you.

So, as we can see there are 5 cities/vertices(a, b, c, d, e) and there are 7 edges/routes

a --- b or b --- a
a --- c or c --- a
a --- d or d --- a
b --- e or e --- b
e --- d or d --- e
e --- c or c --- e
d --- c or c --- d

Now, you will have to figure out a way to visit each city exactly once.

And Breadth first search (BFS) comes to rescue.

Now, if you want to follow Breadth first search (BFS) algorithm, you would have to follow the below steps :

Let us say you are starting from City/Vertex 'c'. And you have to deliver packages to Cities/Vertices a, b, d and e.

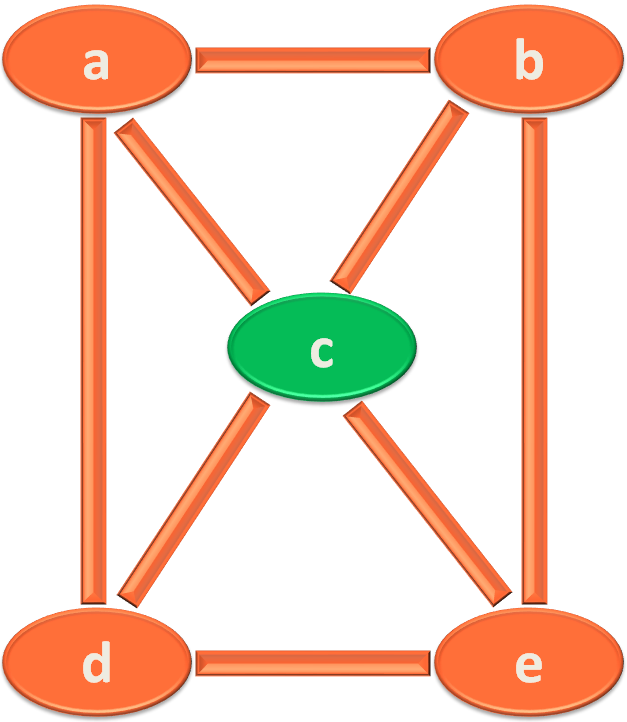
First thing you have to do is, take a queue and place the starting City/Vertex('c' in this case) in that Queue and mark it with Level 0.

At the same time, mark 'c' as visited. But Why?

Simple answer, because we have already visited it.
The next thing you need to do is, try to find out the adjacent Vertices of 'c'(i.e. The Vertices/Cities that are reachable from 'c'). They are 'a', 'd' and 'e'.

Now, you need to take 'c' out of the Queue and place it in the Visited List.

Then insert the adjacent Vertices of 'c'(i.e. 'a', 'd' and 'e') to the Queue and mark them with Level 1.

At the same time, mark 'a', 'd' and 'e' as visited.
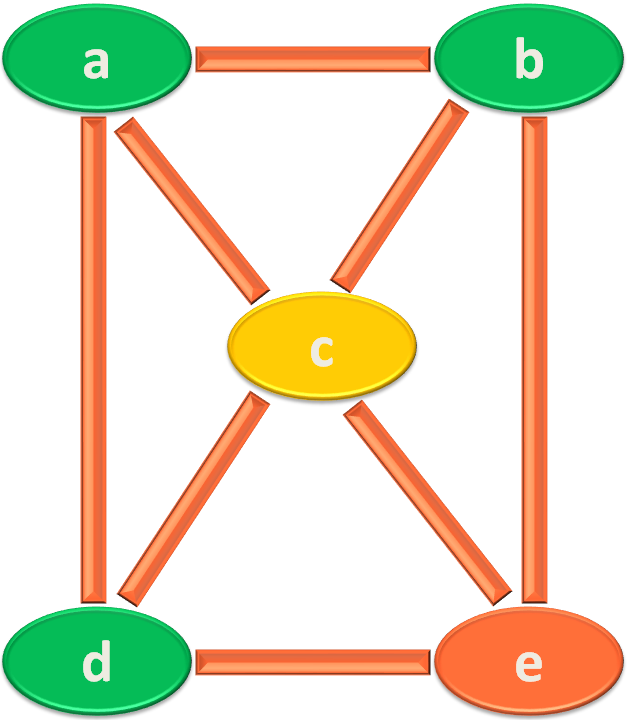
Then you go to the first element of the Queue (It is 'a'). And in the same way, try finding the Adjacent Vertices of 'a'.

The Adjacent Vertices of 'a' are 'b', 'c' and 'd'.

But 'c' and 'd' is already marked as visited. How?

Simple logic! Whoever visits the Queue has to be marked as Visited.

Just have a look at the above 'QUEUE'. 'd' is already present in the Queue and 'c' is in the above 'VISITED' list.

So, we will take 'b' and insert it into the Queue, marking its level to 2.

Also, take 'a' out of the Queue and place it in the visited List.
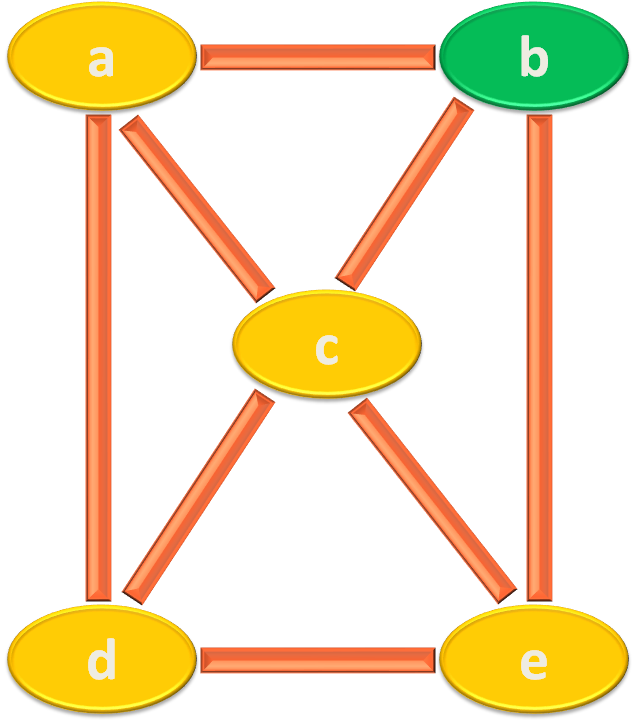
Again, we will take the first element from the queue(i.e. d) and try finding the Adjacent Vertices of 'd'.

The Adjacent Vertices of 'd' are 'a', 'c' and 'e'.

But 'a', 'c' and 'e' are already marked as visited(Discussed in point 1, 2 and 3).

So, we take 'd' out of the Queue and place it in the visited List.
Similarly, we will take the first element from the queue( i.e. e) and try finding the Adjacent Vertices of 'e'.

The Adjacent Vertices of 'e' are 'd', 'c' and 'b'.

Even in this case 'd', 'c' and 'b' are already marked as visited.

So, we will take 'e' out of the Queue and place it in the visited List.
Lastly, we take the only element from the queue(i.e. b) and try finding the Adjacent Vertices of 'b'.

The Adjacent Vertices of 'b' are 'a' and 'e'.

Even in this case both 'a' and 'e' are already marked as visited.

So, we will take 'b' out of the Queue and place it in the visited List.

Now, since the Queue is empty, we can assume all the vertices/cities are visited.

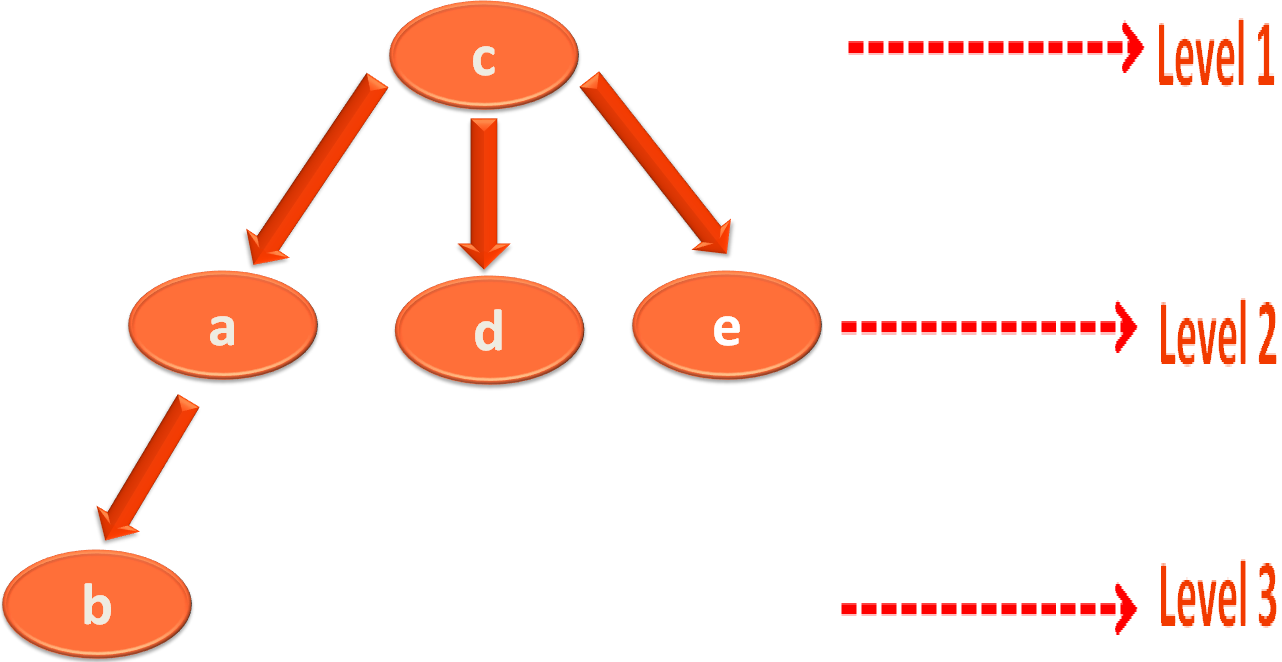
So, we collect all the vertices and their Levels from the Visited List and try drawing a tree based on its Level.

Now, if you look at the above tree. The Source Vertex/City 'c' is at level '0', from where we have started.

Then we came to level 1 and traversed the Vertex/City 'a' and proceeded right visiting Vertex/City 'd' and 'e'.

Then we came to the Level 2 and visited the last Vertex/City 'b'.

Congrats!! You have visited all the Vertex/City exactly once.

Why is the Algorithm called Breadth First Search (BFS)?

If you see the above tree structure. At first, we have started from the source vertex ( i.e. 'c') at Level 0.

Then came down to Level 1 and travelled from 'a' to 'c', i.e. Breadthwise.

And thus, its called Breadth First Search (BFS). Where we travel Breadthwise first and come a Level down.

Efficiency of Breadth First Search (BFS)

Just think, what all do we need for performing Breadth First Search (BFS).

A queue that should be as long as the number of Vertices.
A Graph that should store the Vertices.
A Linked List to store the Adjacent Vertices that shouldn't be more than the number of Vertices.

So, the maximum space needed would be the length of the Vertices.

Space required for Breadth First Search (BFS) : O(V).

Where 'V' is the number of Vertices

Now, let us come to the running time of Breadth First Search (BFS).

To run Breadth First Search, we need to scan the Vertices and also the Edges.

Running time for Breadth First Search (BFS) : O(V+E)

Where V is the number of Vertices.

And E is the number of edges.

❮❮ PREV NEXT ❯❯