Just like Merge Sort, the coding for Quick sort is also based on Recursion. If you don't know recursion, no worries. We will explain Recursion as much as possible.
public class QuickSort {
void sort(int arr[], int left, int right) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
// right part.
int pos = divide(arr, left, right);
sort(arr, left, pos); // Sorts the left part of the array recursively.
sort(arr, pos+1, right); // Sorts the right part of the array recursively.
}
}
int divide(int arr[], int low, int high) {
int pivot = arr[low];
int j = high+1;
int i = low-1;
while(true) {
while (arr[--j] > pivot);
while (arr[++i] < pivot);
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j;
}
}
public static void main(String[] args) {
int arr[] = {7,5,8,6};
System.out.println("Array before Sorting");
for (int i=0; i<arr.length; i++)
System.out.print(arr[i] + " ");
System.out.println();
QuickSort quickSort = new QuickSort();
quickSort.sort(arr, 0, arr.length-1);
System.out.println("Array after Sorting");
for (int i=0; i<arr.length; i++)
System.out.print(arr[i] + " ");
}
}
In the above code we have two methods:
void sort(int arr[], int left, int right)
and
int divide(int arr[], int low, int high)
The first method 'void sort(...)' divides the list into two or more parts.
And the next method 'int divide(...)' returns the position, based on what the list is divided. It calculates the position such that, all the elements less than the pivot element is placed on the left side of the divided list and all the elements greater than or equal to the pivot element is placed on the right side of the divided list.
The execution begins from the 'main(..)' method.
So, initially we will be taking the array,
int arr[] = {7,5,8,6}; And pass it to the sort(...) method,
quickSort.sort(arr, 0, arr.length-1);
void sort(int arr[], int left, int right) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
//right part.
int pos = divide(arr, left, right);
sort(arr, left, pos); // Sorts the left part of the array recursively.
sort(arr, pos+1, right); // Sorts the right part of the array recursively.
}
}
So, we are passing the array 'arr', its starting point i.e. 0(mentioned 'left' inside the parameter of 'sort(...)' method) and the end point i.e. arr.length-1 (mentioned 'right' inside the parameter of 'sort(...)' method).

The array 'arr' contains (7, 5, 8, 6).
And the value of the variable, 'left' is '0'.
The length of the array is 4. Which means (4-1), i.e. 3. So, the value of the variable 'right' is 3.
In the next step we check
if(left < right)
Which means the array length should be more than 1(i.e. If the array length is not more than 1, there is just one element in the array and no further calculation is needed).
Then we calculate the position of pivot element by calling the 'divide(arr, left, mid)' method, so that we can divide the array into two parts.
int pos = divide(arr, left, mid);
Since, our idea is to move the 'pivot' element at position in the array, such that all the elements smaller to the 'pivot' element would be placed at the left of it.
And all the elements greater than the 'pivot' element should be placed at the right hand side of the 'pivot' element.
And that is exactly the work, 'divide(int arr[], int low, int high)' is going to do.
It places the 'pivot' element at the right position and returns the exact position of the 'pivot' element.
int divide(int arr[], int low, int high) {
int pivot = arr[low];
int j = high+1;
int i = low-1;
while(true) {
while (arr[--j] > pivot);
while (arr[++i] < pivot);
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j;
}
}
All we are doing in the above case is,
int divide(int arr[], int low, int high)
Getting the elements of the array in arr[].
And the 'low' and 'high' variables contains '0' and '3'.
In the next step, we get the pivot element(The first element in the array will be the pivot element).
int pivot = arr[low];
Now, since arr[low] or arr[0] contains '7'. The pivot variable 'pivot' will have '7'.

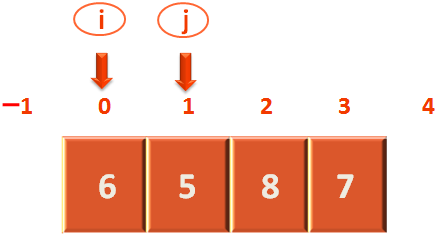
Next, we will make 'j' to point to a position right after the last element.
int j = high+1;
So, the value of 'j' becomes

Similarly, we will make 'i' to point to a position just before the first element.
int i = low-1;
So, the value of 'i' becomes
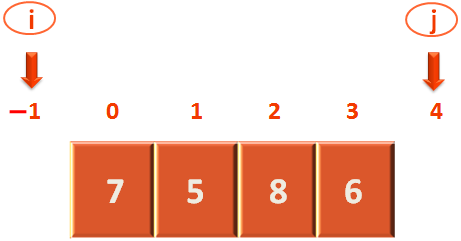
Now, let's check the main chunk of code from above:
while(true) {
while (arr[--j] > pivot);
while (arr[++i] < pivot);
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j;
}
There are three 'while' loops.
while(true)
while (arr[--j] > pivot);
while (arr[++i] < pivot);
The outer loop
while(true)
only exits when 'i' and 'j' cross each other.
Let us see how.
The while loop runs indefinitely,
while(true)
And the above 'while' loop only stops when the 'if' condition is not satisfied and the control goes to the 'else' statement,
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j;while(true) Which means when 'i' is greater than or equal to 'j', it returns 'j' and exits.
In other words, when 'i' and 'j' cross each other, The above 'while' loop (i.e. while(true)) stops.
Now, let us come to the inner 'while' loop,
while (arr[--j] > pivot);
So, the idea is to move 'j' towards the left until it finds an element less than the pivot element.
And, the above 'while' loop exactly does the same.
It keeps on decrementing 'j', and the loop continues until it finds an element less than the pivot element.

Let us demonstrate in brief,
while (arr[--j] > pivot);
while (arr[--j] > pivot);
When we replace 'j' and 'pivot' with its actual values,
while (arr[3] > 7);
In the above case, the value of j becomes 3 as we are decrementing the value of 'j' first, then we are going to compare it.
And we can see that arr[3] has '6', i.e. less than the pivot element i.e. 7.
So, the control comes out of the while loop, pointing 'j' to the 4th location.

Similarly, let us come to the inner 'while' loop,
while (arr[++i] < pivot);
So, the idea is to move 'i' towards the right until it finds an element less than the pivot element.
Even in this case, the above 'while' loop does the same.
It keeps on incrementing 'i' until it finds an element less than or equal to the pivot element.

Let us demonstrate in brief,
while (arr[++i] < pivot);
while (arr[++i] < pivot);
When we replace 'i' and 'pivot' with its actual values,
while (arr[0] > 7);
And we can see that arr[0] has '7', i.e. equal to the pivot element i.e. 7.
So, the control comes out of the while loop, pointing 'i' to the 1st location.
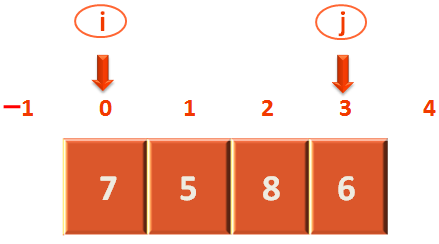
Now, since we are done with the 'while' loops. It's time to check the 'if' block (That helps to exit from the outer loop).
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j;
The above 'if' block checks, if 'i' and 'j' have crossed each other or not (i.e. Have a look at the above array block. Until 'i < j', 'i' and 'j' have not crossed each other).
In the above case 'i' is less than 'j'. Since, the value of 'i' is 0 and the value of 'j' is 6.
So, we get into the 'if' block. And all it does is swaps the values of arr[i] and arr[j].
So, we swap the values of arr[0] and arr[3].
And the new array contents after swapping becomes :
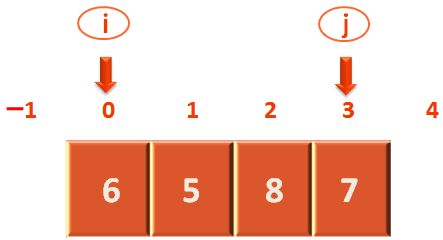
We are not yet done as the return statement in the 'else' part has still not executed.
else
return j; We are not yet done as the return statement in the 'else' part has still not executed.
else
return j; So, we continue with the outer loop,
while(true)
And reach the inner 'while' loop,
while (arr[--j] > pivot);
And, the idea is to move 'j' towards the left until it finds an element less than or equal to the pivot element.
And, the above 'while' loop exactly does the same.
So, after looping through. The 'while' loop stops at the second position when it finds the element '5' in the second location in the array is less than the pivot element.
Similarly, the control comes to the next while loop dealing with 'i'.
while (arr[++i] > pivot);
And, the idea is to move 'i' towards the right until it finds an element greater than or equal to the pivot element.
And, the above 'while' loop exactly does the same.

And, after looping through. The 'while' loop stops at the third position when it finds the element '8' in the third location in the array is greater than the pivot element.
And we can see that 'i' and 'j' have crossed each other.
So, if we look at the 'if' statement,
if (i < j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
} else
return j; The value of 'i' is 2 and the value of 'j' is 1.
And finally the control comes to the else statement and returns the value of 'j' i.e. 1.
Now, let us divide the above array based on the value of 'j'.

And BINGO ! That's what we wanted. All the elements less than the pivot element i.e. 7 is on the left side. And all the elements greater than or equal to the pivot element i.e. 7 is on the right side.
And the next piece of code will take the above two parts and calculate it further.
Let us see how?
In the next line, the value of 'j'(i.e. 1) will be assigned to the 'pos' variable.
Let us take a look at the 'sort(..)' method again,
void sort(int arr[], int left, int right) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
//right part.
int pos = divide(arr, left, right);
sort(arr, left, pos); // Sorts the left part of the array recursively.
sort(arr, pos+1, right); // Sorts the right part of the array recursively.
}
}
The 'pos' variable, from the above code contains 1 (i.e. The value returned from 'sort(int arr[], int left, int right)')
int pos = divide(arr, left, right);
Now, comes the fun part. When we encounter the line,
sort(arr, left, pos);
We call the sort(...) method from the sort(...) method itself. And this is called recursion. Where a method keeps on calling itself until it comes to an end. And it maintains an internal stack which is hidden from the programmer.
It might look a little complex, but trust me it is quite simple. Just stay with me.
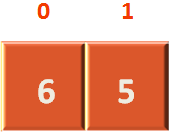
All we are doing in this step is, taking the left hand side of the array and passing it to the 'sort()' method.
i.e. If we substitute the values of 'sort(arr, left, pos);'
We can see 'left' variable has '0' and 'pos' variable has 1.
Which means, the 'sort()' method is going to operate on the left side of array.
And if we come to the next line,
sort(arr, pos+1, right);
The above line will deal with the right part of the array.
i.e. If we substitute the values of 'sort(arr, pos+1, right);'
We can see 'pos+1' variable would be '2'(Since value of 'pos' variable is 1) and 'right' variable has 3.
Which means, this time the 'sort()' method is going to operate on the right side of array.

Let us see it in brief, how the array is partitioned at every step :
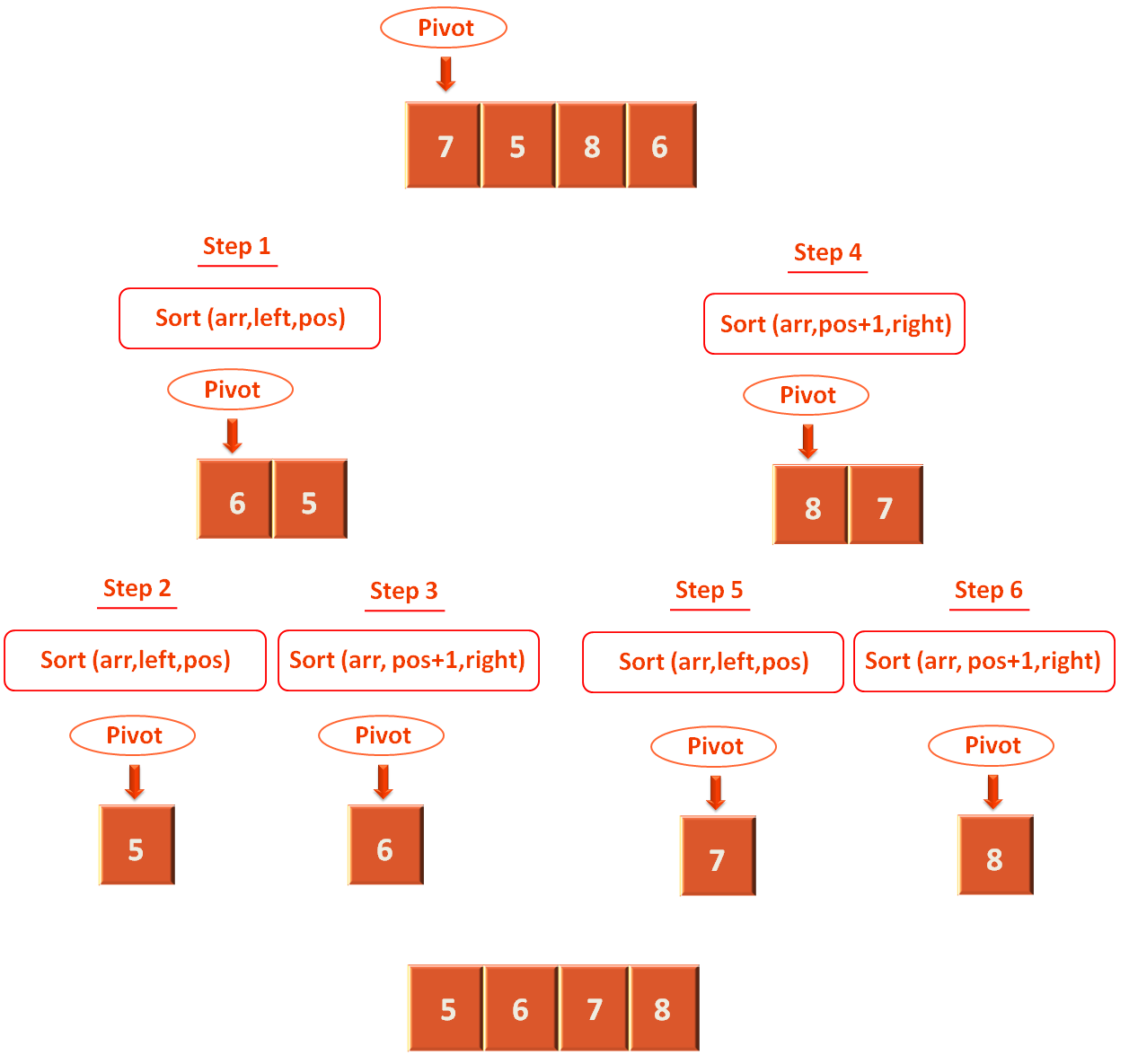
The above 6 step process is the best way to understand the code.
We have the array with values 7, 5, 8, 6.
From which we select the pivot element(i.e. 7) and call the 'divide(arr, left, right)' method. Based on this pivot element, the array is divided into two parts. Such that all the elements less than the pivot element will be placed on the left half and all the elements greater than or equal to the pivot element will be placed on the right part.
if(left < right)
Now, if we combine all the parts. We get a sorted array.
There are complicated processes to understand the efficiency/running for Quick Sort. But we will keep it simple, so that it becomes simple to understand and we can calculate the running time for any algorithm this way.
Let's say we are lucky.
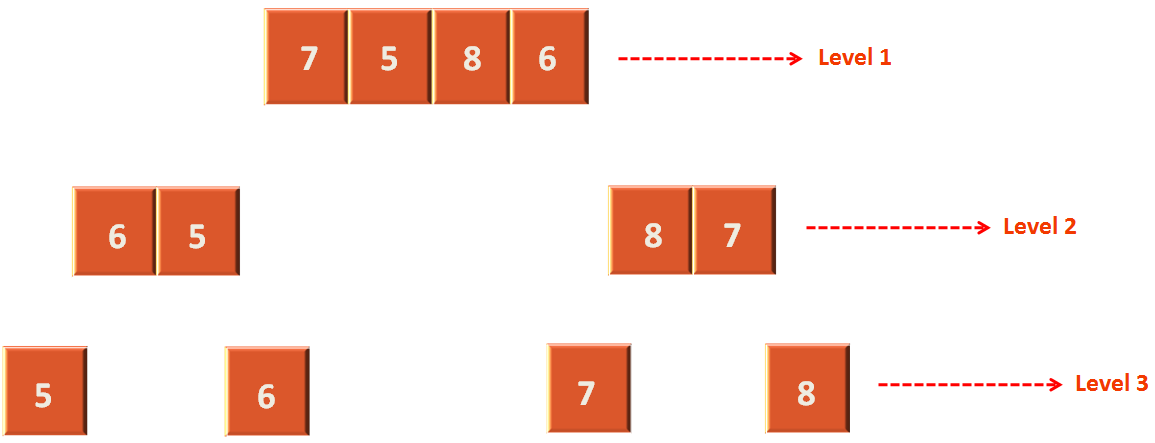
As as we have seen in the above case the array is divided exactly into two parts at all steps.
Thus, at each step the 'divide(...)' method will take n times at each level. And how many levels are there. There are three levels or log n.
So, if we combine we get the,
Best case running time : O(n log n )
Now, lets say we are quite unlucky.
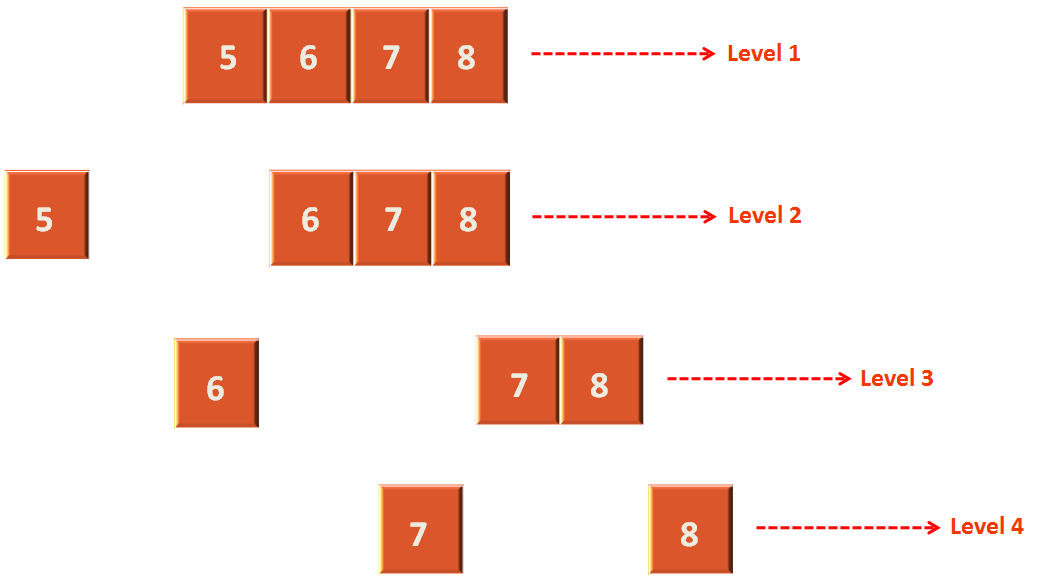
In the above array has 4 levels. In other words there are n levels. And also the divide(...) method is going to run n times at each level.
So, the
Worst case running time : O(n**2)
Average case running time : O(n log n)