ASYMTOTIC NOTATIONS

In the previous lesson we have seen, how to find the Time and Space Complexity of an Algorithm.

Now, in this lesson we will see a way to represent it.

To make it a little simpler. Let's say, in the previous lesson, we have got a running time of an Algorithm as Linear Time or 'n'. But there has to be a way to represent it.

And yes! There is a way to represent it. And it is called as 'Asymptotic Notation'.

There are three types of 'Asymptotic Notations' :

Big-oh or 'O' - Is called as Upper Bound.
Big-omega or 'Ω' - Is called as Lower Bound.
Theta or '𝚹' - Is called as Average Bound.

Before we explain all the three types of 'Asymptotic Notations', let us write all the complexities we can possibly have, starting from lowest to the highest.

1, log n, √n, n, n log n, n² , n³ ,...., 2ⁿ , 3ⁿ ,..., nⁿ

So, the lowest time would be taken by a constant operation i.e. 1. Then comes log n and so on as mentioned above.

Note : Just a little warning before we start. We would be writing some mathematical functions below. Just don't get panicked, we would explain each and everything in simple words.

Now, let us look at all the three types of 'Asymptotic Notations' in detail :

Big-oh or 'O'

The Big-oh or 'O' is called as Upper Bound. Let us understand Big-oh or 'O' with the below function.

So, the function :

f(n) = O(g(n))

Is true, if and only if there exists +ve constants c and n₀ .

Such that,

f(n) <= c * g(n) for all n >= n₀

Let us simplify the above statement.

Just remember f(n) is how we represent a function in Mathematics.

Now, let us suppose,

f(n) = 5 * n

Just recall, in the previous lesson/tutorial, we have calculated the time complexity 'n'. And here, we have just multiplied 'n' with a constant say 5.

i.e.

f(n) = 5 * n

Now, according to the description of Big-oh or 'O', the above function f(n) is equal to Big-oh of g(n) or O(g(n)). If there exists +ve constants c and n₀ .

Such that,

f(n) <= c * g(n) for all n >= n₀

So, let us say,

g(n) = n and c = 5.

Then the above condition,

f(n) <= c * g(n)

Can also be written as,

f(n) <= 5 * n

As, we have supposed g(n) = n and c = 5.

But there is also one more condition,

n >= n₀

Nothing to worry about the above condition. It just says the value of 'n' should be greater than '0'.

Now, say you have calculated the time complexity of a program and it is (5 * n).

Now, the time complexity can be written as 'O(n)'. Removing '5' from 'n'.

And why is that?

Because we have seen, by definition,

f(n) = O(g(n)),

If f(n) <= c * g(n) is true.

And

f(n) = 5 * n

Now, matching it with the above condition we get,

g(n) = n and c = 5.

Because,

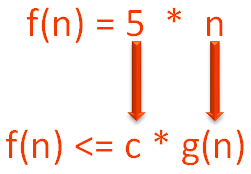
So, the condition,

f(n) = O(g(n))

Is satisfied and we can write,

f(n) = O(n)

Since g(n) = n.

Fair enough!

Now, let us understand, why Big-oh or 'O' is called as Upper Bound?

To understand this, let us rewrite all the complexities we can possibly have, starting from lowest to the highest.

1, log n, √n, n, n log n, n² , n³ ,...., 2ⁿ , 3ⁿ ,..., nⁿ

As explained above, the lowest time would be taken by the constant operation i.e. 1. Then comes 'log n' and so on as mentioned above.

Now, in the above case, we have calculated the time complexity as 'n' and the Big-oh or 'O' of 'n' is,

O(n)

And the strange fact is that for Big-oh or 'O', we can write any complexities that is greater than 'n'.

n, n log n, n² , n³ ,...., 2ⁿ , 3ⁿ ,..., nⁿ

Let us simplify it.

We have calculated the time complexity as 'n'. And the Big-oh or 'O' could be 'n' or any complexity that is greater than 'n'.

i.e.

O(n) or O(nlog n) or O(n² ) and all the complexities that are greater than 'n'.

n, n log n, n² , n³ ,...., 2ⁿ , 3ⁿ ,..., nⁿ

And this is exactly why Big-oh or 'O' is called as Upper Bound.

Seems weird! Right?

Well! That is how it is.

But just because you are given the flexibility to write anything that is greater than 'n'.

You should not be writing those. Not because they are not right, but they just don't fit in.

If the complexity you have calculated is 'n'. You should always write the Big-oh or 'O' as O(n).

Big-omega or 'Ω'

The Big-omega or 'Ω' is called as Lower Bound.

Now, the concept of Big-omega or 'Ω' is almost same as Big-oh or 'O'. Completely self explanatory.

But for the sake of learning, let us understand the below function for Big-omega or 'Ω'.

So, the function :

f(n) = Ω(g(n))

Is true, if and only if there exists +ve constants c and n₀ .

Such that,

f(n) >= c * g(n) for all n >= n₀

Let us simplify the above statement with the same example we have used above.

i.e.

f(n) = 5 * n

Now, the above function when written using Big-omega or 'Ω', it becomes,

f(n) = Ω(n)

The explanation is exactly same as Big-oh or 'O'.

Now, why is Big-omega or 'Ω' called as Lower Bound?

Again the explanation is almost same as the upper bound concept of Big-oh or 'O'.

i.e. All the complexities that are lower than 'n' is applicable for Big-omega or 'Ω'.

1, log n, √n, n

So, Big-omega or 'Ω' of 'n' can be written as

Ω(n) or Ω(√n) or Ω(log n) or Ω(1)

But the best practice is to write Big-omega or 'Ω' of 'n' as Ω(n).

Theta or '𝚹'

The Theta or '𝚹' is called as Average Bound.

Again, the concept of Theta or '𝚹' is almost same as Big-oh or 'O'. Completely self explanatory.

Now, for the sake of learning, let us understand the below function for Theta or '𝚹'.

So, the function :

f(n) = 𝚹(g(n))

Is true, if and only if there exists +ve constants c₁ , c₂ and n₀ .

Such that,

c₁ * g(n) <= f(n) <= c₂ * g(n) for all n₀ >= n

Let us simplify the above statement with the same example we have used above.

i.e.

f(n) = 5 * n

Now, the above function when written using Theta or '𝚹', it becomes,

f(n) = 𝚹(n)

The explanation is exactly same as Big-oh or 'O'.

Now, why is Theta or '𝚹' called as Average Bound?

Again the explanation is almost same as the upper bound concept of Big-oh or 'O'.

i.e. All the complexities that are equal to 'n' is applicable for Theta or '𝚹'.

So, Big-omega or 'Ω' of 'n' can only be written as

𝚹(n)

❮❮ PREV NEXT ❯❯