BINARY SEARCH

So far, we have seen that we can search an element using Linear Search in O(n) time.

To reduce that time, here comes 'Binary Search'. It can search the List/Array in O(log n) time. But it comes with a condition.

The condition is, the List/Array has to be sorted.

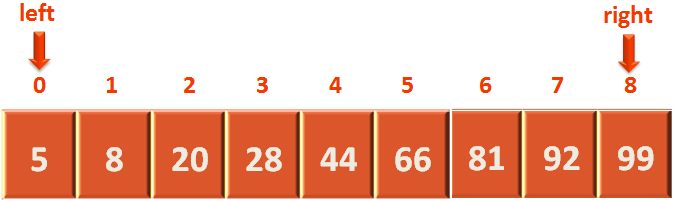
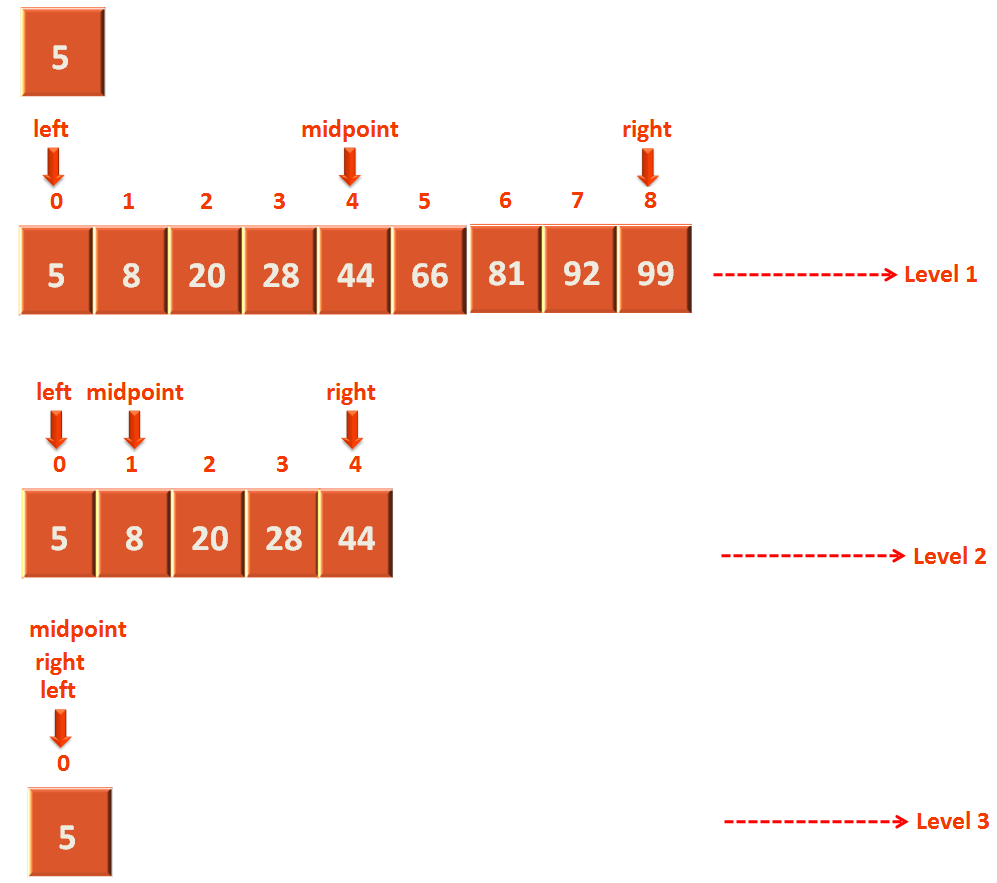
To understand Binary search. Let us take the below array :

There are 9 numbers in the above array.

Say, we need to find the number '5' from the array.

As we can see, the array is sorted.

We will make the 'left' point to the very first location. And the value of 'left' will be 0.

And make 'right' point to the last location. We will make the value of 'right' as 8.

Now, we will apply the below steps :

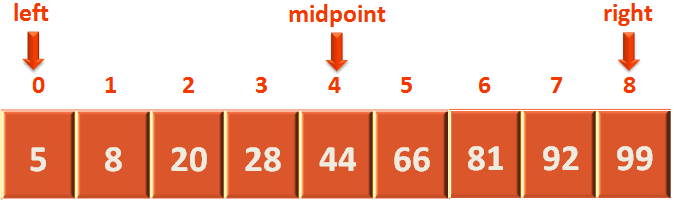
At first, we will calculate the mid point of the array.

midPoint = (left + right) / 2
midpoint = 4 (We will 4 instead of 4.5)

Then we will check, if the element we are searching for (i.e. 5), is present in the 'midpoint' or not.

In this case, there is '44' in the 'midpoint'.

Which is not equal to 5.

Now, since we have found, the element '5' is not present in the 'midpoint'. We will check, if the element '5' is greater than or less than the element in the 'midpoint'.

In this case '5' is less than '44'(i.e. The element in the midpoint).

So, we can assume that '5' lies in the left side of the midpoint.

Wondering why ?

Because, we know that the array is sorted. Now, if '5' is smaller than 'midpoint' element '44', '5' should definitely be on the left side of the 'midpoint' element '44'.

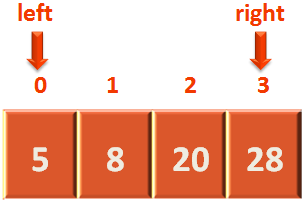
Next, we will discard all the elements to the right of the 'midpoint', including the 'midpoint'.

As we already know that the element '5' lies in the left side of the midpoint.

Next, let us repeat the same process. i.e. Calculating the 'midpoint' from the above chunk of array.

For that, let us mark the end of the above chunk to 'right' instead of 'midpoint-1'.

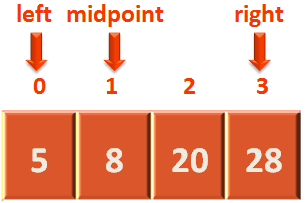
Next, we calculate the midpoint.

midPoint = (left + right) / 2
midpoint = 1.5 = 1

Again, we check if the element '5', resides in the 'midpoint' or not?

In this case, there is '8' in the 'midpoint', that is not equal to '5'.

So, we check, if '5' is less than '8'(i.e. The element in the 'midpoint') or not?

In this case, '5' is less than '8'.

So, we can assume '5' lies in the left side of '8'. And we discard the right side of 'midpoint', along with the 'midpoint'.

Now, the interesting thing is 'right' and 'left' points to the same location.

Let us calculate the 'midpoint' again.

midPoint = (left + right) / 2
midpoint = 0

Now, if we check, the element '5' is there in the 'midpoint' or not. And we find that '5' is present in the 'midpoint'.

And thus we found, the element '5' is present at array index 0.

Let us look at the overall structure.

Element to be searched,

Looking at the above structure, let us figure out the running time.

Running time for Binary Search

We have claimed that the running time for Binary search is O(log n).

How do we calculate log n?

There are 9 elements in the above array. For a clean and easy calculation let us consider the above array has 8 elements.

We know 8 can also be represented as (2) ³ .

Now, we can say,

8 = (2) ³

And,

8 = (2) ³ is exactly equivalent to also be represented as log₂ 8 = 3.

Now since, we have considered the above array has 8 elements. Which has a running time of log 3.

Note : Just remember, n represents, how many elements the array actually has. In our case the array has 8 elements. And O(log n) represents, how many times the loop has ran.So, in our case log n or log 8 is 3. So, all we have to do is prove that the loop ran 3 times.

Let's prove it :

At every step, we have calculated the 'midpoint' that took O(1) time.

And to find the element, there are 3 Levels or we can say, Binary Search ran 3 times.

So, Binary Search ran 3 times. And thats all we had to prove.

Running time of Binary Search : O(log n)

❮❮ PREV NEXT ❯❯