INSERTION SORT CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

public class Sort {

void insertionSort(int arr[]) {

int n = arr.length;
for (int i=1; i < n; i++) {

int key = arr[i];
int j = i-1;

/* Insert arr[i] or key into the sorted sequence arr[0...i-1] */

while(j>=0 && arr[j] > key) {

arr[j+1] = arr[j];
j--;
}

arr[j+1] = key;
}
}

public static void main(String args[]) {

int arr[] = {5, 3, 6, 2, 1, 4};

int arr[] = {5, 3, 6, 2, 1, 4};
int arr[] = {5, 3, 6, 2, 1, 4};

for(int i=0; i < arr.length; i++) {

System.out.println(arr[i]+", ");
}
}
}

We are just bothered about the 'void insertionSort(int arr[])' method, where the sorting logic is defined.

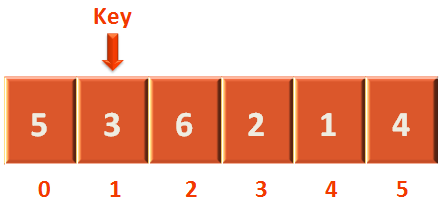
We have the array

int arr[] = {5, 3, 6, 2, 1, 4};

Which we have passed to the 'insertionSort(..)' method.

In the 'insertionSort(..)' method, we have taken the count of the elements of the array.

int n = arr.length;

Then, we are running a 'for' loop which will iterate the array starting from the second element till the last element.

for (int i=1; i < n; i++)

And we are setting the 2nd element of the array as the key.

int key = arr[i];

i.e. Content of arr[1] is the 'key' initially. So, the value of 'key' is 3.

Then we make the value of 'j' as 'i-1'.

int j = i-1;

That's because we need to compare the key (i.e. arr[1]) with the left hand side elements (i.e. arr[0], where the value of j is 0) of the key. .

And that is where the 'while' loop comes into picture. Which takes care of the comparison of the 'key' with the left hand side of the array..

while(j>=0 && arr[j] > key) {

arr[j+1] = arr[j];

j--;
}

Note : Refer to the above diagram.

The above 'while' loop is quite self explanatory. Where, we are getting into the 'while' loop if the 'key'(i.e. value of arr[1] that is '3') is less than arr[j] (i.e. value of arr[0] that is '5').

And we are replacing the value of arr[j+1](i.e. arr[1]) with arr[j] (i.e. arr[0]).

arr[j+1] = arr[j];

Now, arr[1] contains 5. Also arr[0] contains 5, but arr[0] should be 3.

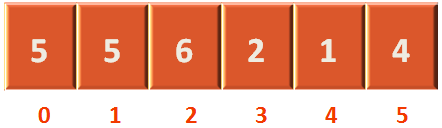
So, how the value of arr[0] is replaced by 3.

That happens when we get out of the loop, when the condition j>=0 is met by while loop.

Note : Remember the control comes out of while loop when j is less than 0. Which means when the value of j becomes -1.

And set the value of arr[0] with the key (i.e. 3).

arr[j+1] = key;

Since, -1+1 is 0. So the above is arr[0] = key.

And finally, arr[0] is set to 3.

Similar, process follows for the entire loop.

Efficiency / Running time of Insertion Sort

If we consider the Insertion Sort Algorithm, there are two loops. First is the 'for' loop. And inside the 'for' loop there is a 'while' loop.

The 'for' loop executes n times(Assuming the array contains n elements).

Now, for each iteration of 'for' loop, the 'while' loop also executes 'n' times in worst case.

Which means for 1st iteration of 'for' loop,

'while' loop runs 1 time.

Similarly, for 2nd iteration of 'for' loop,

'while' loop runs 2 times.

Similarly, for nth iteration of 'for' loop,

'while' loop runs n times.

So, the running time is close to n*n or n².

So, in worst case the running time is O(n²).

Note : Worst case is the scenario where the array elements are all sorted in descending order. i.e. 6, 5, 4, 3, 2, 1.

And in best case the running time is O(n).

Note :Best case is the scenario where the array elements are all sorted in ascending order.

❮❮ PREV NEXT ❯❯