

AVL trees are the height balanced Binary Search Trees.
To understand AVL Trees, let us relook at Binary Search Trees and its drawbacks.
And as we have seen, the time taken to search an element from a Binary Search Tree is the height of the Binary Search Tree or O(h) or it can be O(log n) in case of a balanced Binary Search Tree.
Where 'h' is the height of the Binary Search Tree and 'n' is the number of elements in the Binary Search Tree.
Now, let us consider the below Binary Search Tree:
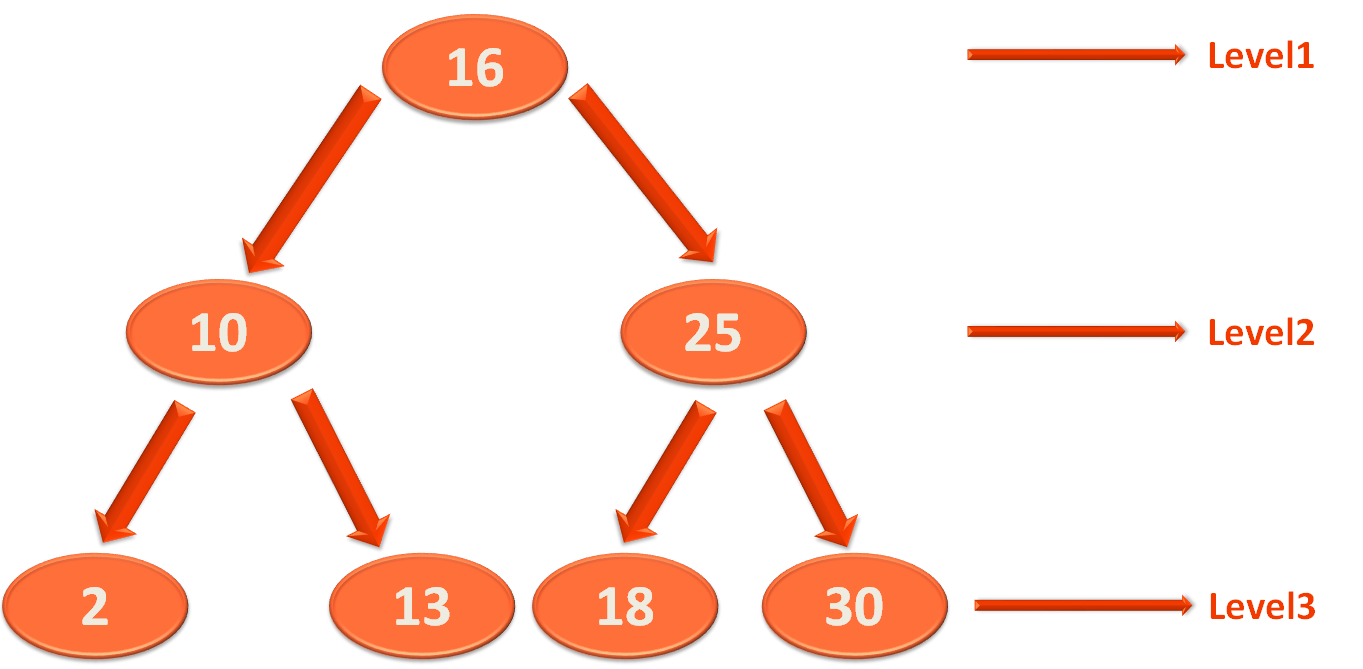
So, the height of the above tree is 3.
Now, if we want to search '30' from the above Binary Search Tree. Within 3 iterations, we will be able to find the number '30'.
But how?
First we come to the root element '16' and find that '30' is greater than '16'. So, it should be somewhere in the right subtree.
Then we find '25' as the root element in the right subtree. And we find that '30' is greater than '25'. So, '30' should be somewhere in the right subtree of '25'.
And when we come to the right subtree we find the number '30' is present there.
Be it any number, we want to find from the above Binary Search Tree. It can be done at max in 3 iterations. And 3 is the height of the above Binary Search Tree.
Which is also log n. Where 'n' is the number of elements in the above Binary Search Tree, i.e. 7.
Now, the above tree was a balanced tree.
But what if we have a Binary Search Tree that is not balanced?
Let us take the example of the below Binary Search Tree.
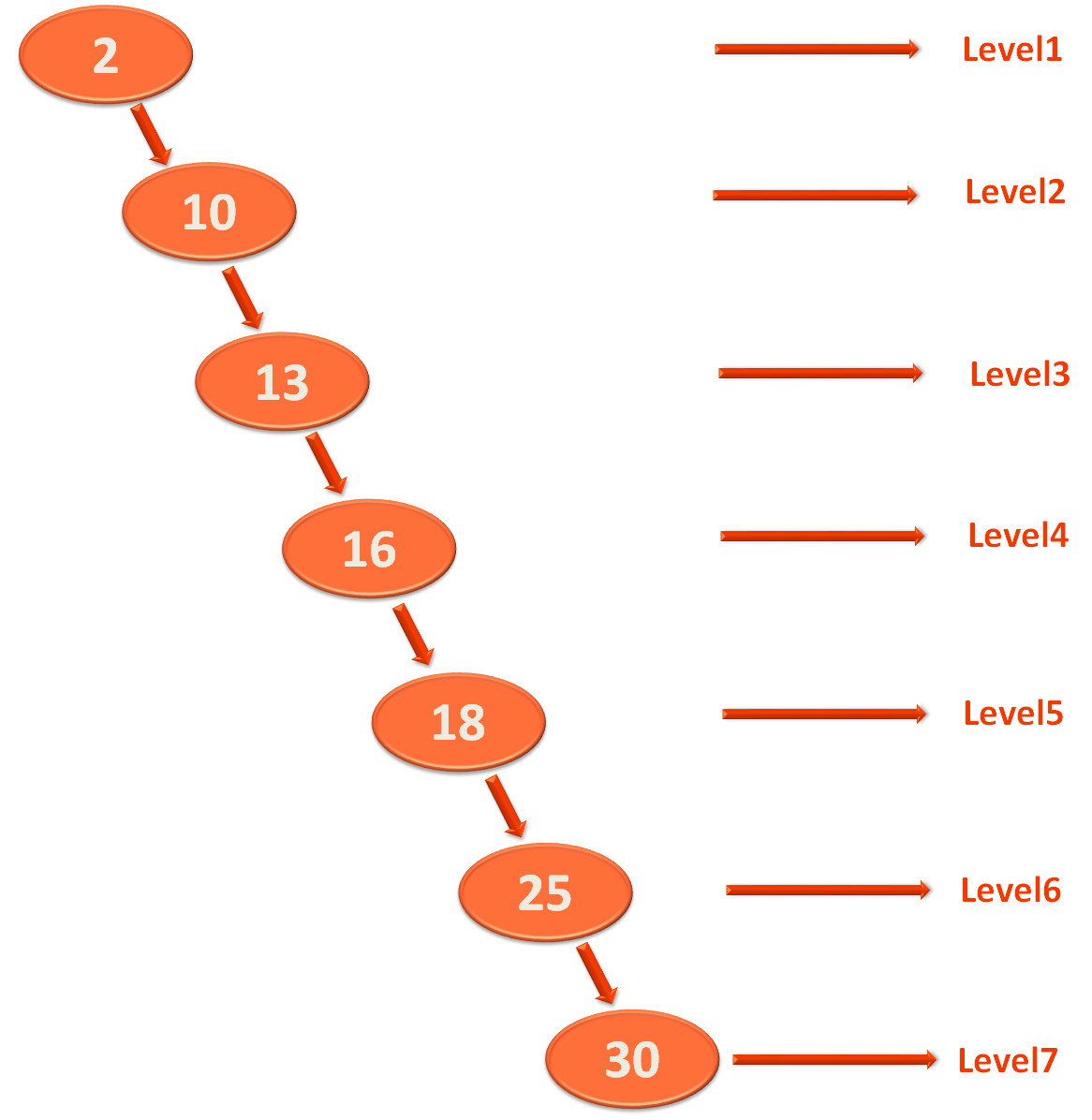
Now, the above tree is also a Binary Search Tree. As all the right elements are greater than its root.
And in this case the height of the Binary Search Tree is same as the number of elements in the Binary Search Tree.
i.e. The number of elements in the Binary Search Tree is 7 and the height of the Binary Search Tree is also 7.
Now, if we want to search for the element '30' from the above Binary Search Tree. We have to iterate 7 times(As we know, the time taken to search an element from a Binary Search Tree is the height of the Binary Search Tree or O(h)).
And in this case, the time taken to search for the element '30' would be O(n) and not O(log n).
This is because the Binary Search Tree,

Is height balanced. And the Binary Search Tree,
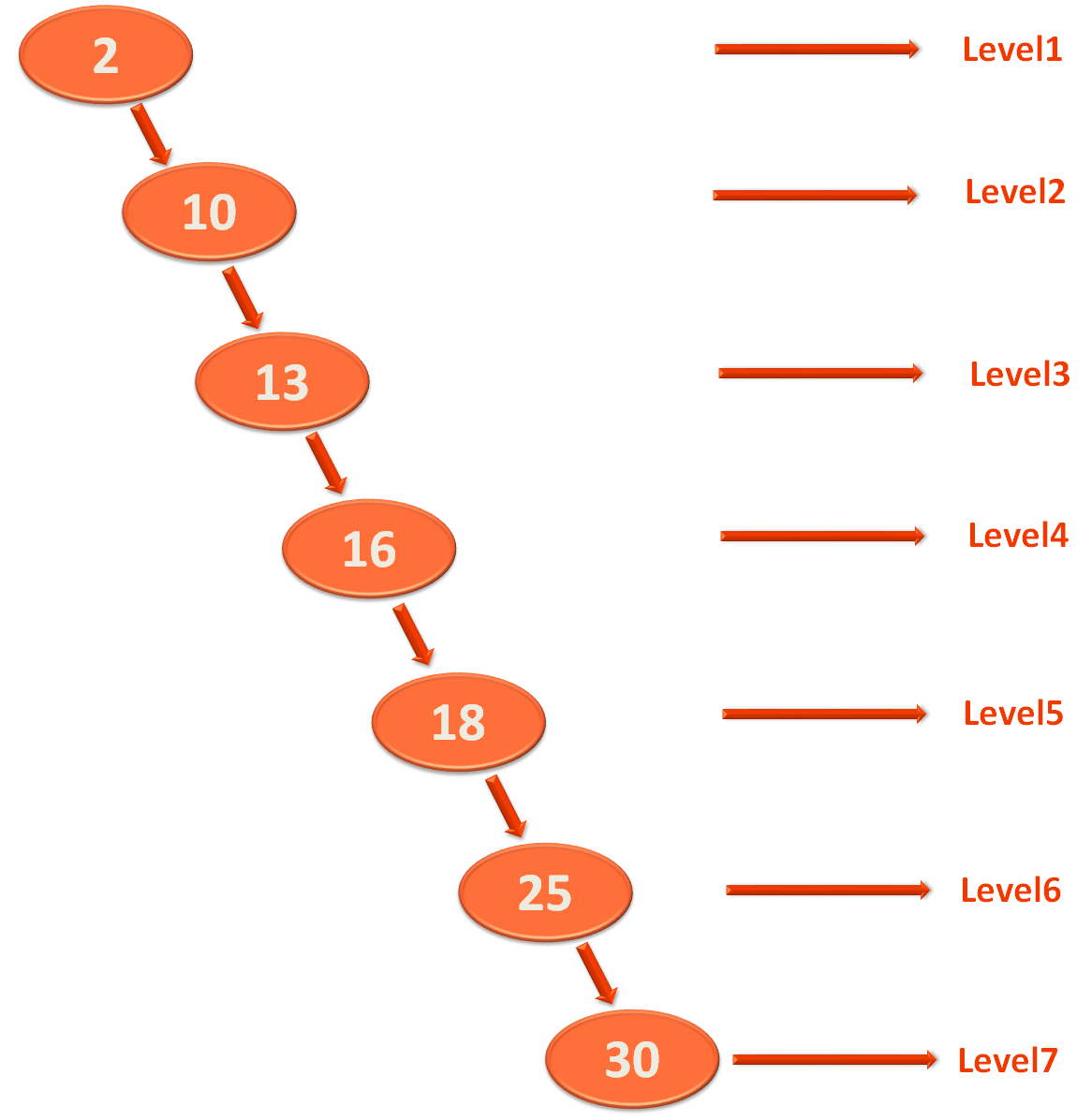
Is not height balanced.
Click here to see the Explanation for Height Balanced Binary Search Tree.
What is the exact thing that comes to your mind, when we say a 'Balanced Binary Tree'?
Well! A Binary Tree that is Balanced.
Now, to check if a Binary Tree is balanced or not. We need to check the depth of left and right sub tree of the parent element.
And if the difference of depth is 0 or 1, it is a 'Balanced Binary Tree', else it is not.
Let us clear it with the below example :

Now, what is the depth of the left sub tree of Parent Node 'A'?
The left sub tree of Parent Node 'A' is,
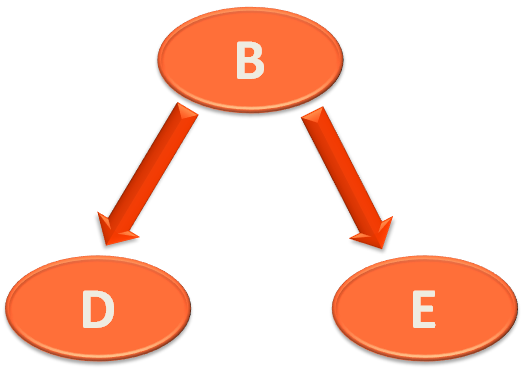
And the depth of 'B' is 1.
Next, let us calculate the depth of the right sub tree of Parent Node 'A'.
The right sub tree of Parent Node 'A' is,
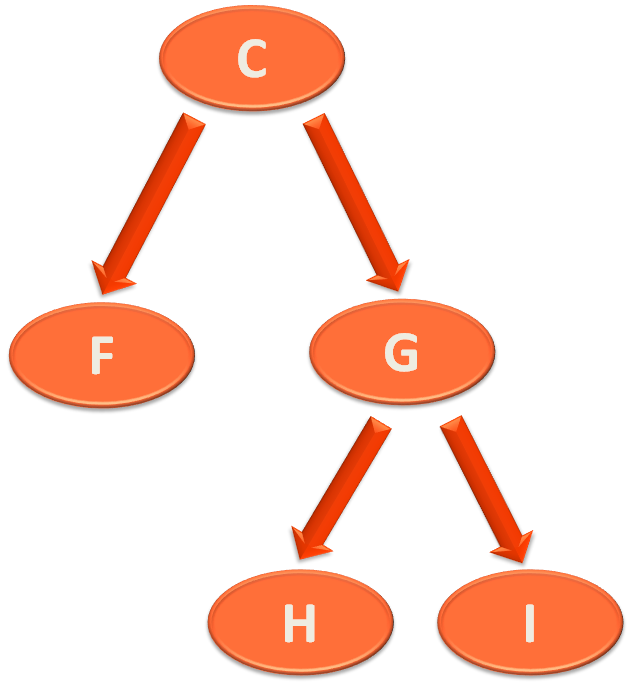
And the depth of 'C' is 2.
Now, if we find the difference between 2 and 1.
And the difference is 1. So the above tree is a 'Balanced Binary Tree'.
Now let us take another example :
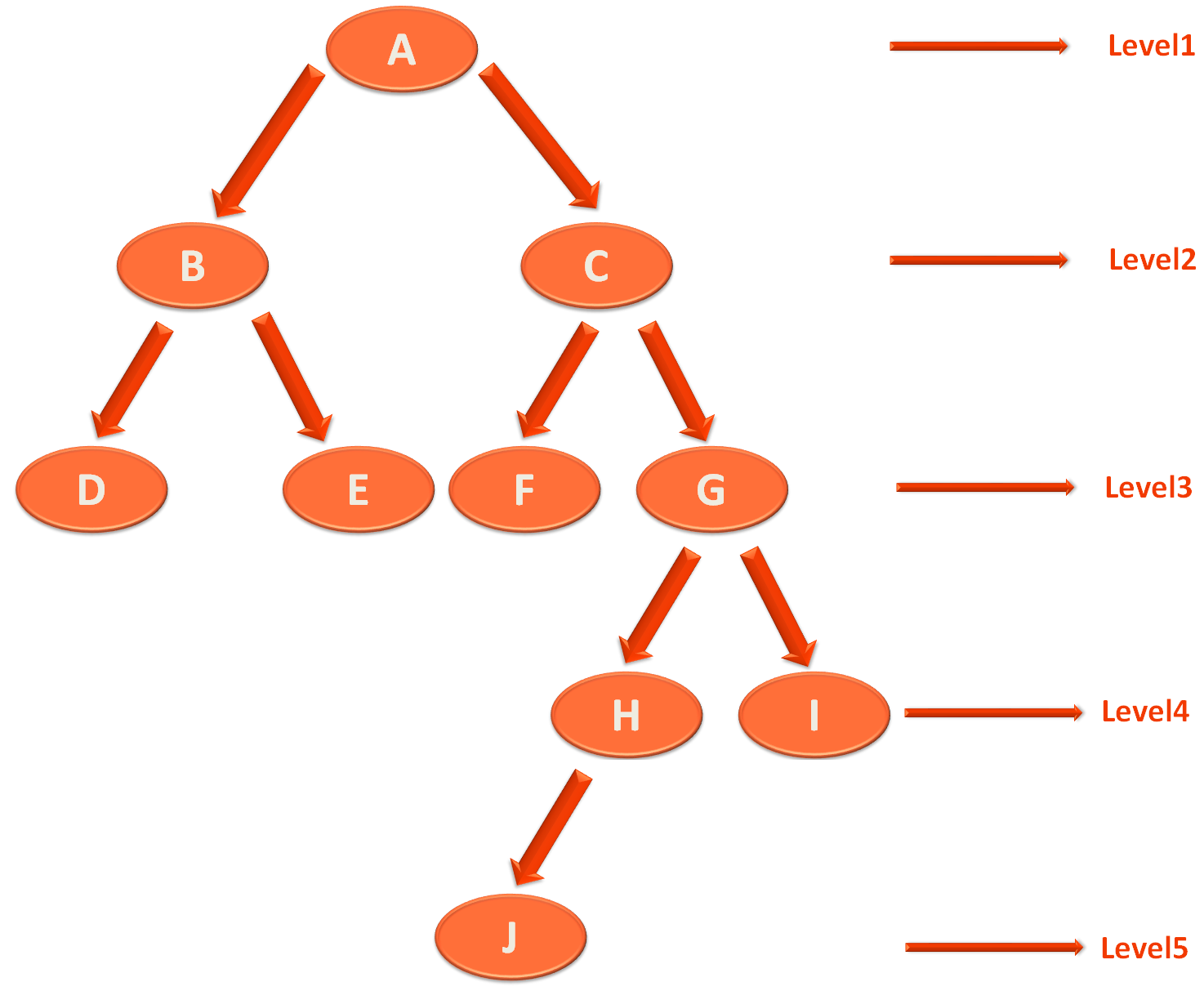
Similarly, let us calculate the depth of the left sub tree of Parent Node 'A'.
The left sub tree of Parent Node 'A' is,
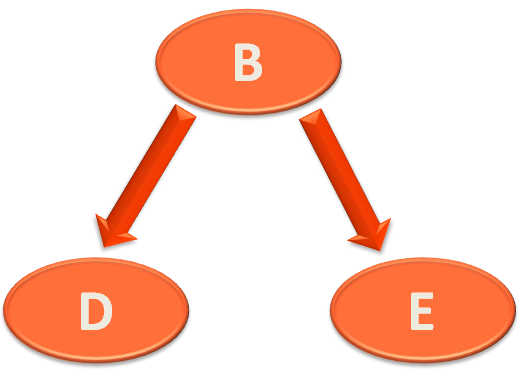
And the depth of 'B' is 1.
Next, let us calculate the depth of the right sub tree of Parent Node 'A'.
The right sub tree of Parent Node 'A' is,

And the depth of 'C' is 3.
Now, if we find the difference between 3 and 1.
And the difference is 2. So the above tree is a not a 'Balanced Binary Tree'.
And Since, the Binary Search Tree was not height balanced. The searching time was O(n) instead of O(log n).
Now, if by some way we can convert an unbalanced Binary Search Tree into a balanced one. We can reduce the searching time from O(n) to O(log n).
And this is exactly where 'AVL Trees' comes to rescue.
You can consider AVL Tree as Binary Search Tree that is balanced. In other words AVL Trees are height balanced Binary Search Trees.
An AVL Tree balances a Binary Search Tree by performing some rotations based on something called 'Balance Factor'.
Where a 'Balance Factor' is calculated by finding the difference between 'Height of Left SubTree' and 'Height of Right SubTree'.
Now, if the 'Balance Factor' is equal to -1, 0, 1. The Binary Search Tree is Height Balanced.
And if the 'Balance Factor' is not -1, 0, 1. Then we need to perform rotation to balance the tree(Which we will be seeing below).
Say for example, if we consider the below Binary Search Tree,
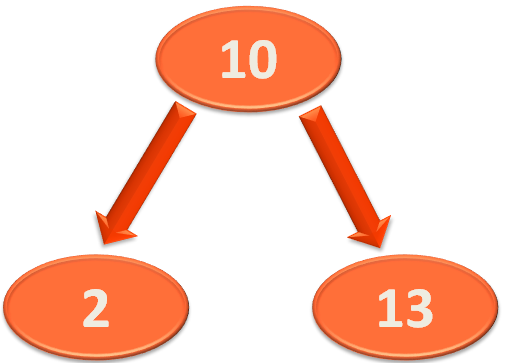
The 'Balance Factor' of the Root Element '10' is
Since, 'Height of Left SubTree' & 'Height of Right SubTree' is 1.
The 'Balance Factor' of the Left Element '2' is 0. As it has no child element present.
Similarly, The 'Balance Factor' of the Right Element '13' is also 0. As it has no child element as well.
Now, since all the three elements in the above Binary Search Tree has the 'Balance Factor' 0. So, the above Binary Search Tree is said to be balanced.
Next, let us see a Binary Search Tree that in not Balanced.

Let us start checking the 'Balance Factor' from the bottom element of the right subtree.
So, the bottom element of the right subtree is '11'. And since it has no child, the 'Balance Factor' of the element '11' is '0'.
Now, let us go a step up the Tree and find the 'Balance Factor' of the element '12'.
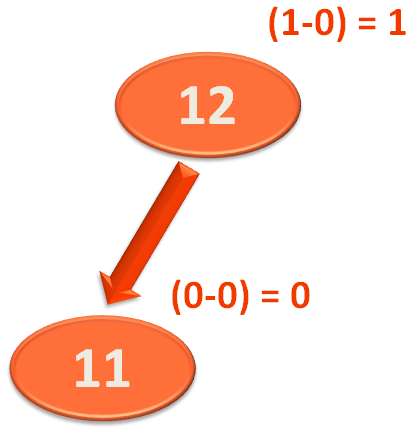
And as we can see, '12' has only 1 element at the left. And no element at its right.
So, the 'Balance Factor' of the element '12' would be,
So, the 'Balance Factor' of the element '12' is 1. And is balanced.
Now, we will go a step up to the element '13' and try finding the 'Balance Factor'.
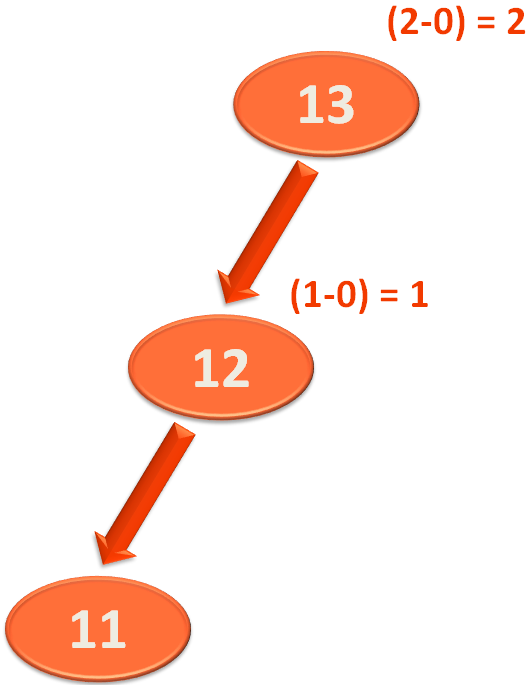
And as we can see, '13' has only 2 elements at the left. And no element at its right.
So, the 'Balance Factor' of the element '13' would be,
So, the 'Balance Factor' of the element '13' is 2. And it is unbalanced.
So, we need to find a mechanism to balance it.

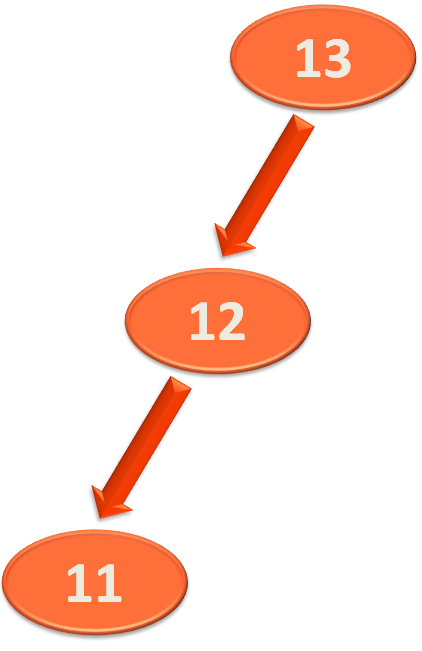
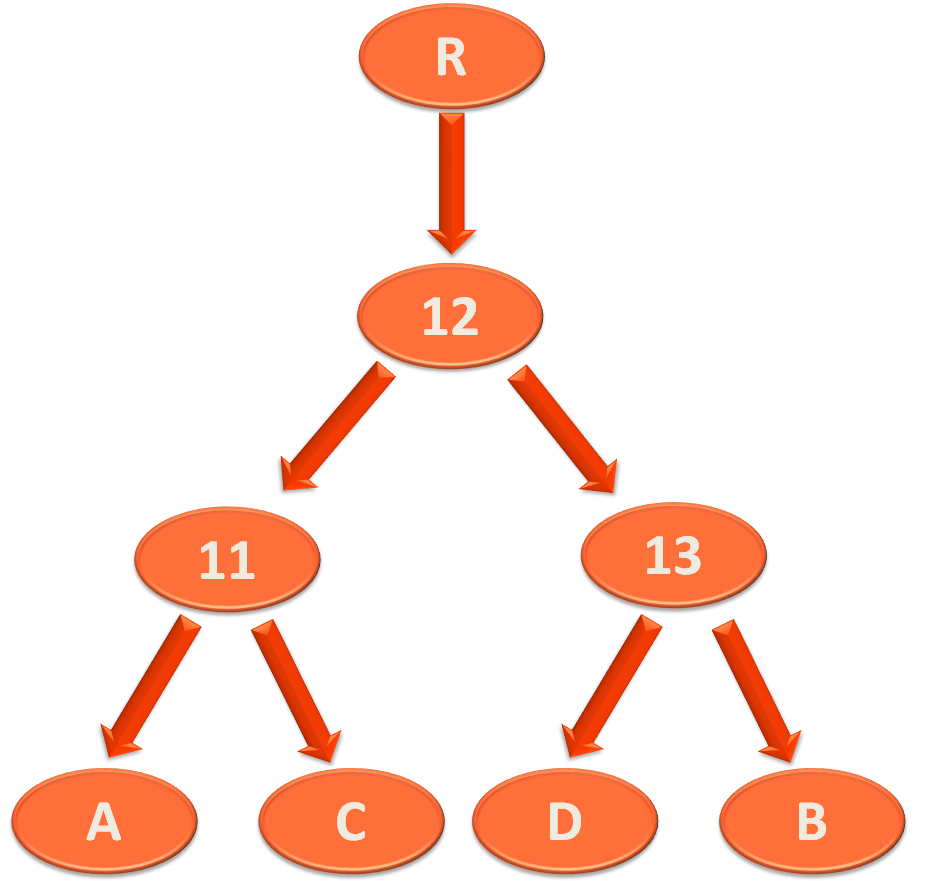
And what we do is, make the root element '13', the right child of '12'.
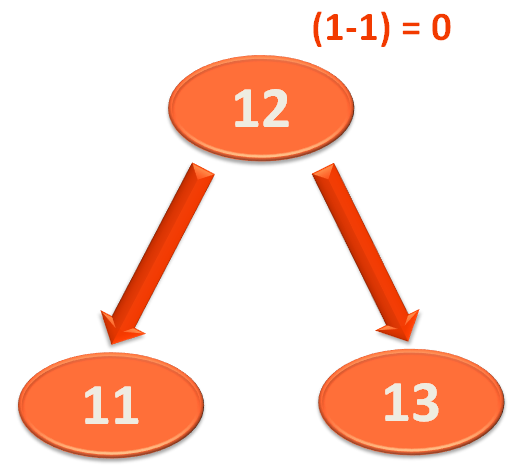
Now, '12' becomes the root element of this subtree and the elements '11' and '13' becomes the left and right element of '12'.
Now, if we see the whole tree,

Now, since we are done balancing the elements 11, 12, 13. We can go a step up the tree and reach the root element '10'.
So, the height of the left subtree of root element '10' is 1.
And the height of the right subtree is 2.
So the 'Balance Factor' for the root element '10' is -1. And is balanced.
Now, that we are done with all the elements of the right subtree and the root itself. We are left with left subtree.
As as we can see that there is just one element in the left subtree i.e. 2. And '2' has no children. So, the 'Balance Factor' of 2 is 0.
And as we can see the above tree is balanced.
Now, if we look at the above operation. We have performed only one type of rotation.
i.e.
to
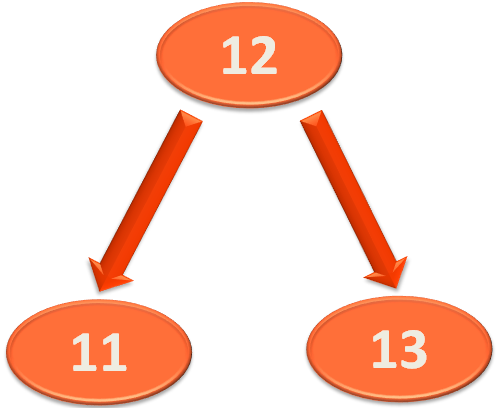
But there can be other types of rotations that could be performed as well. Let us see those in detail:
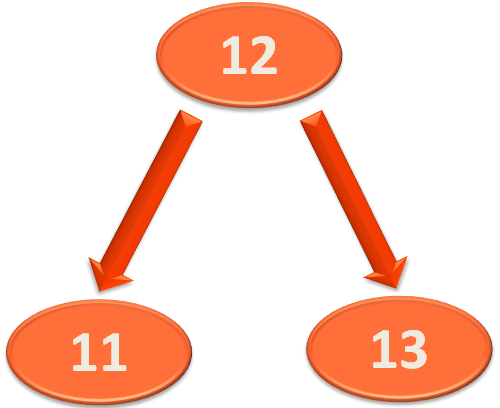
Right rotate is what we have already seen. Let's relook it once again with the same elements.
And to 'Right Rotate' it, we will take the element '13' and rotate it towards the right. And the element '12' becomes the root and '13' becomes its right child.
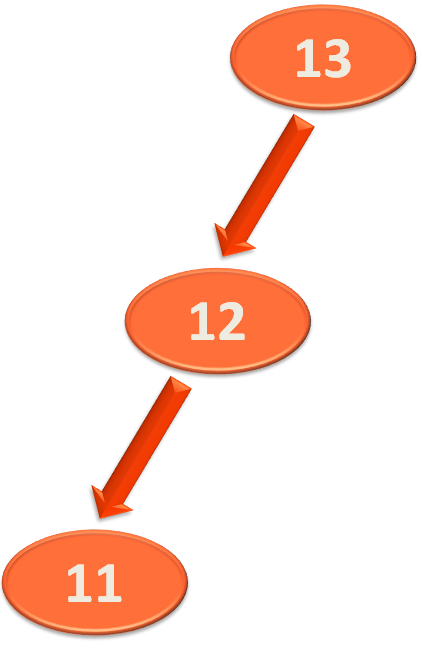
And even after rotation, it is still a Binary Search Tree.
Now, let us look at the bigger picture. i.e. It could be possible that the Binary Search Tree,

Is a part of a bigger Binary Search Tree.

Let us say that the element '13' has a root element, say 'R' and a right element, say 'A'.
Also, the element '12' has a right element, say 'B'.
And the element '11' has left element, say 'C' and right element, say 'D'.
Note that we have put 'R', 'A', 'B', 'C' and 'D' instead of numbers to focus on rotation.
But 'R', 'A', 'B', 'C' and 'D' are actually numbers.
Now, if we perform right rotation on,
'13' becomes the right child of '12' and we get,
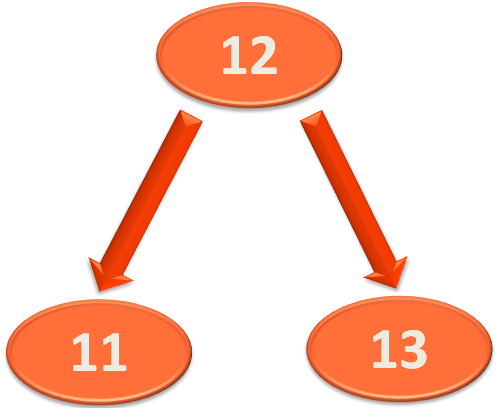
But we have seen that the right child of '12' was 'B'. And due to right rotation, the element '13' became the right child of '12'.
So, 'B' becomes the left child of '13'. And 'A' was already the right child of '13'.
And '12' gets connected to the root element 'R'.
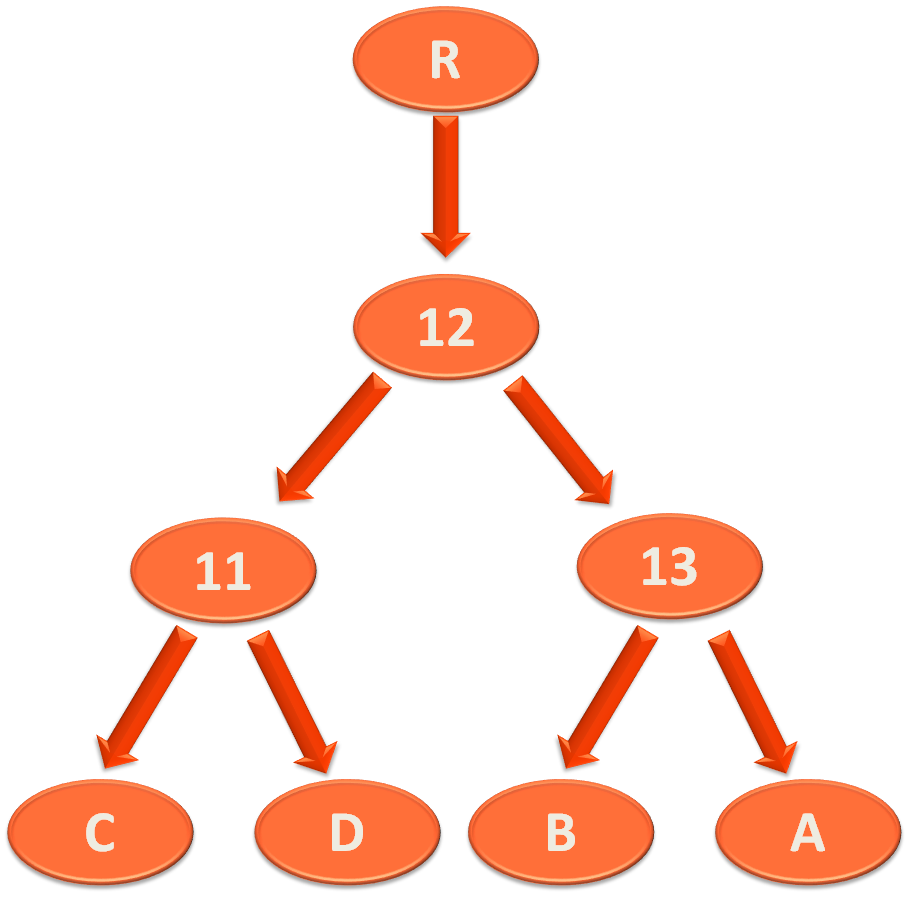
And this is exactly how right rotation is performed.
Let us see how Left rotation is performed with the below example.

This time we rotate the tree towards the left and '11' becomes the left child of '12'.

Now, let us look at the bigger picture. Where the below Binary Search Tree,
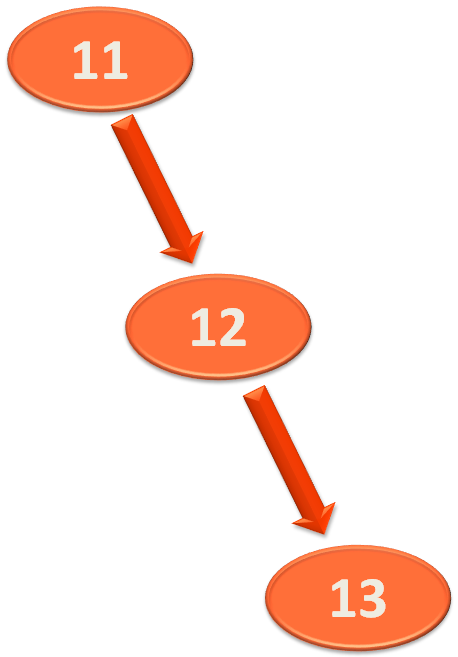
Is a part of a bigger Binary Search Tree.

Now, if we perform left rotation on,
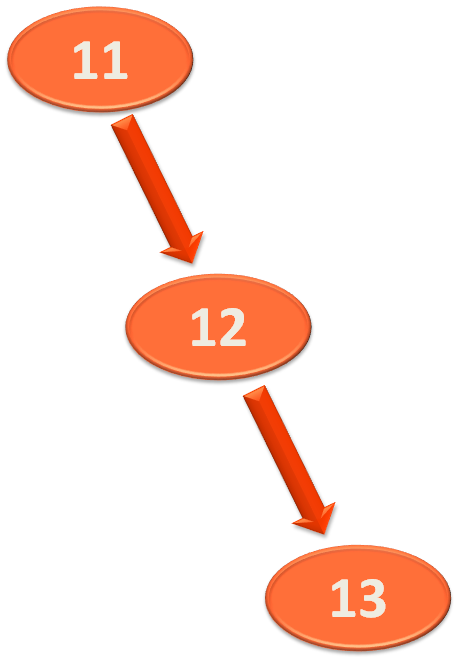
'11' becomes the left child of '12', 'B' becomes the right child of '11' and '12' is connected to the root element 'R'.
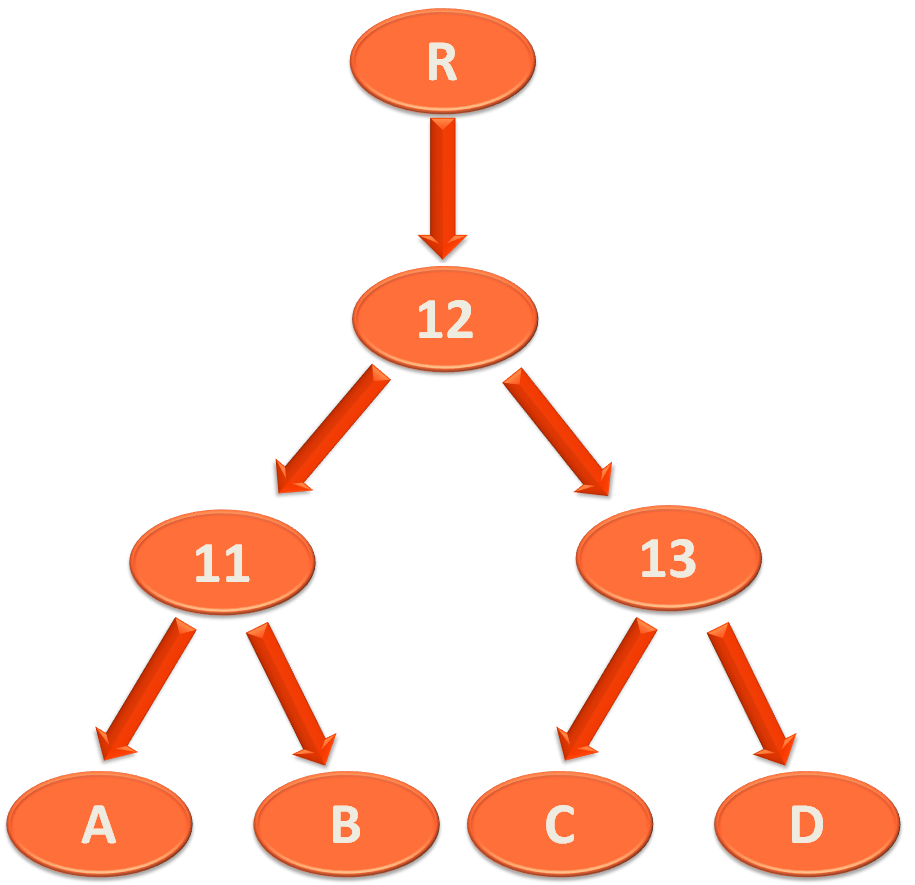
Say there can be a scenario like the below example,

In the above case, neither left rotation or right rotation alone will balance the above Binary Search Tree.
In this case, what we will do is take the lower half of the tree,
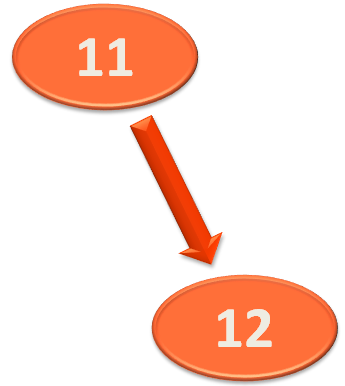
And perform left rotation on it.
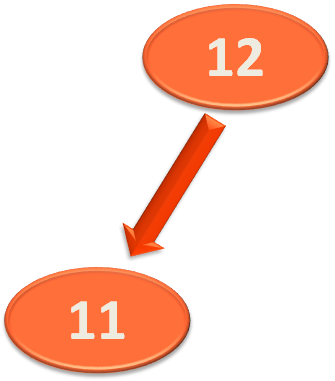
And '11' becomes the left child of '12'.
So, if we see the entire tree,
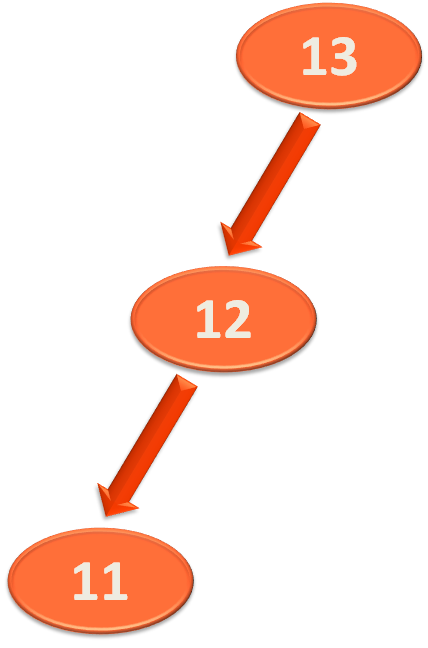
Now, we are in the shape to perform a right rotation on the above Binary Search Tree.

Now, let us look at the bigger picture. Where the below Binary Search Tree,

Is a part of a bigger Binary Search Tree.
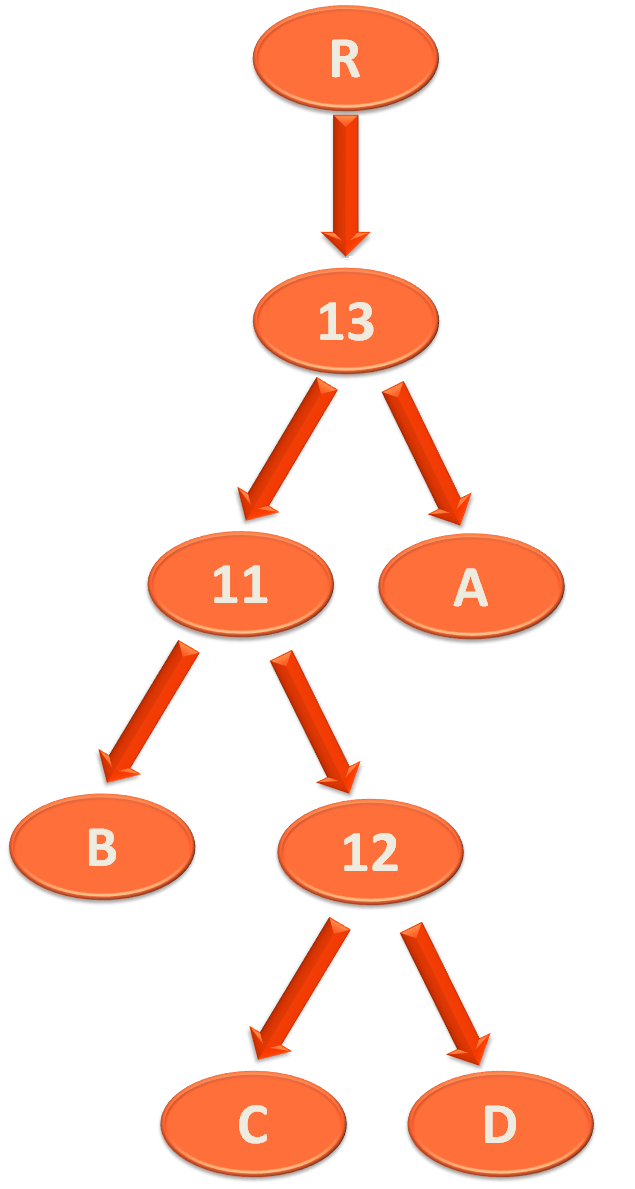
And we have to perform Left-Right rotation to balance the above tree.
So, at first we perform the Left Rotation,

Then perform the Right Rotation,

Similarly, there can be a scenario like the below example,

And in the same way, neither left rotation or right rotation alone will balance the above Binary Search Tree.
And so, will do is take the lower half of the tree,

And perform right rotation on it.

And '13' becomes the right child of '12'.
So, if we see the entire tree,
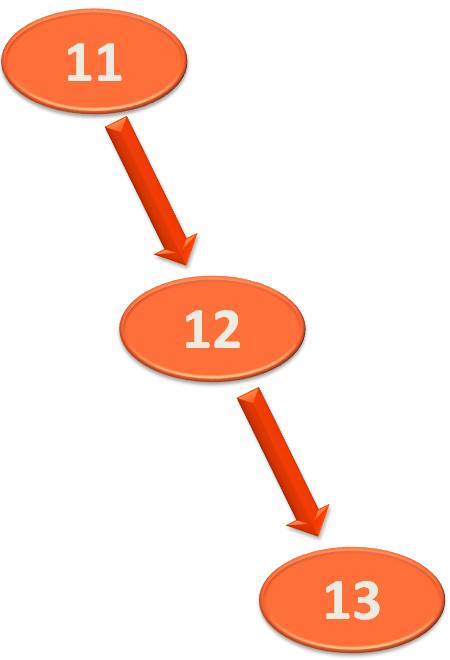
Now, we can perform left rotation on the above tree.
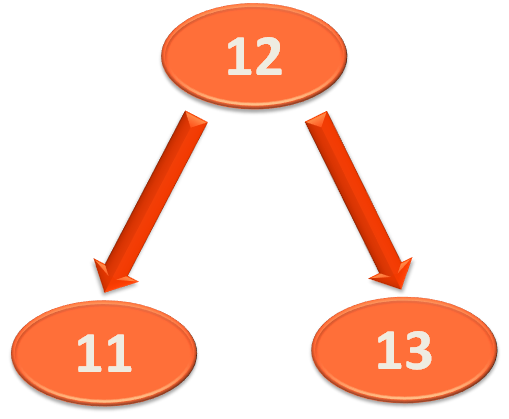
And we got the above tree by Right-Left Rotation.
Now, let us look at the bigger picture. Where the below Binary Search Tree,

Is a part of a bigger Binary Search Tree.

And we have to perform Right-Left rotation to balance the above tree.
So, at first we perform the Right Rotation,
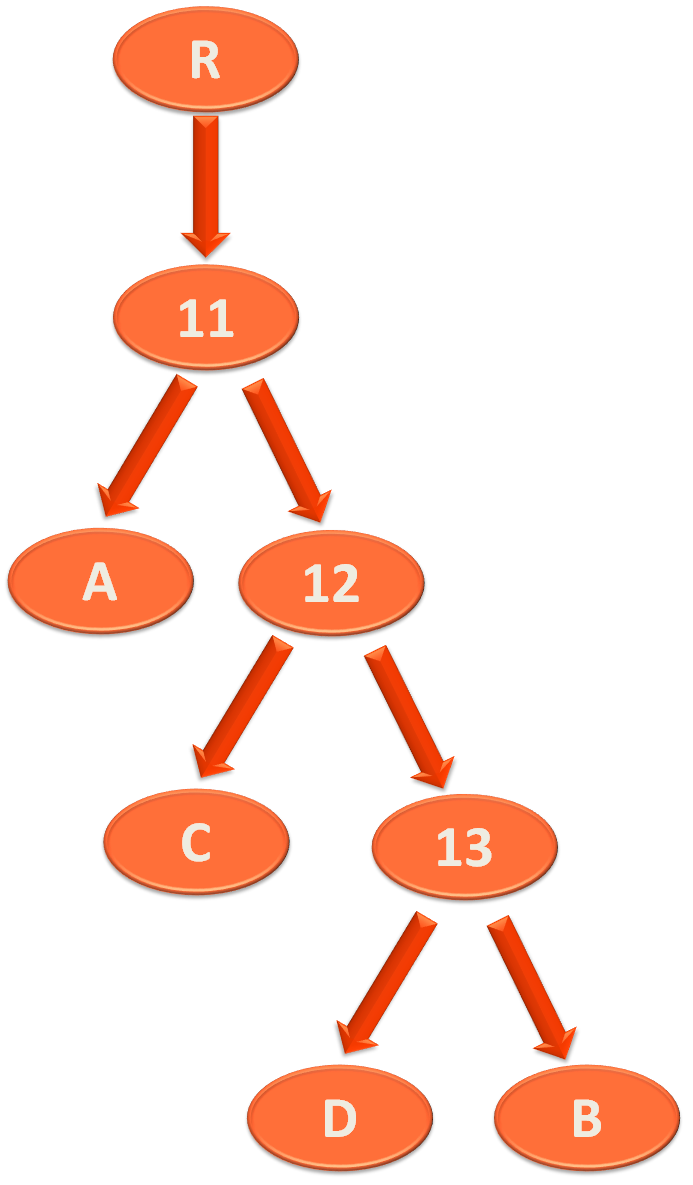
Then we perform the Left rotation.
So, the above Binary Search Tree is balanced.
Now, what if we try to add a new element to the Binary Search Tree. Don't you think it might become unbalanced? Well in some cases it might.
Let us see, the addition of a new element in a Binary Search Tree.
Let us say, we have the below Binary Search Tree, with the Balance Factor for each Nodes.
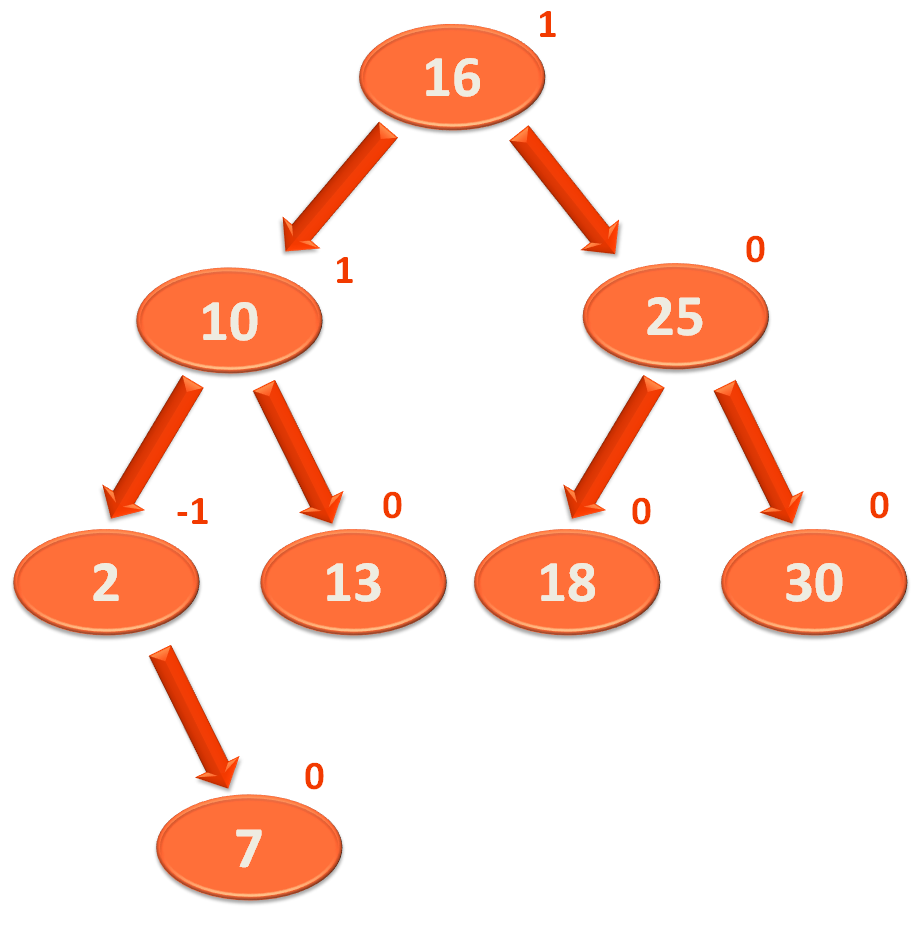
So, the above Binary Search Tree can be said to be balanced as the Balance Factor are either -1, 0 or 1 for all the Nodes.
Now, let us say that we want to insert the element '8' into the above Binary Search Tree.
So we check the element '8' with the root element '16'.
And find that '8' is less than '16'. So, it should be somewhere in the left subtree.
Then we check the element '8' with the root element of the left subtree i.e. 10.
And by comparing '8' with the elements, we find that '8' should be placed at the right side of the element '7'.

Now, if we calculate the Balance Factor again,
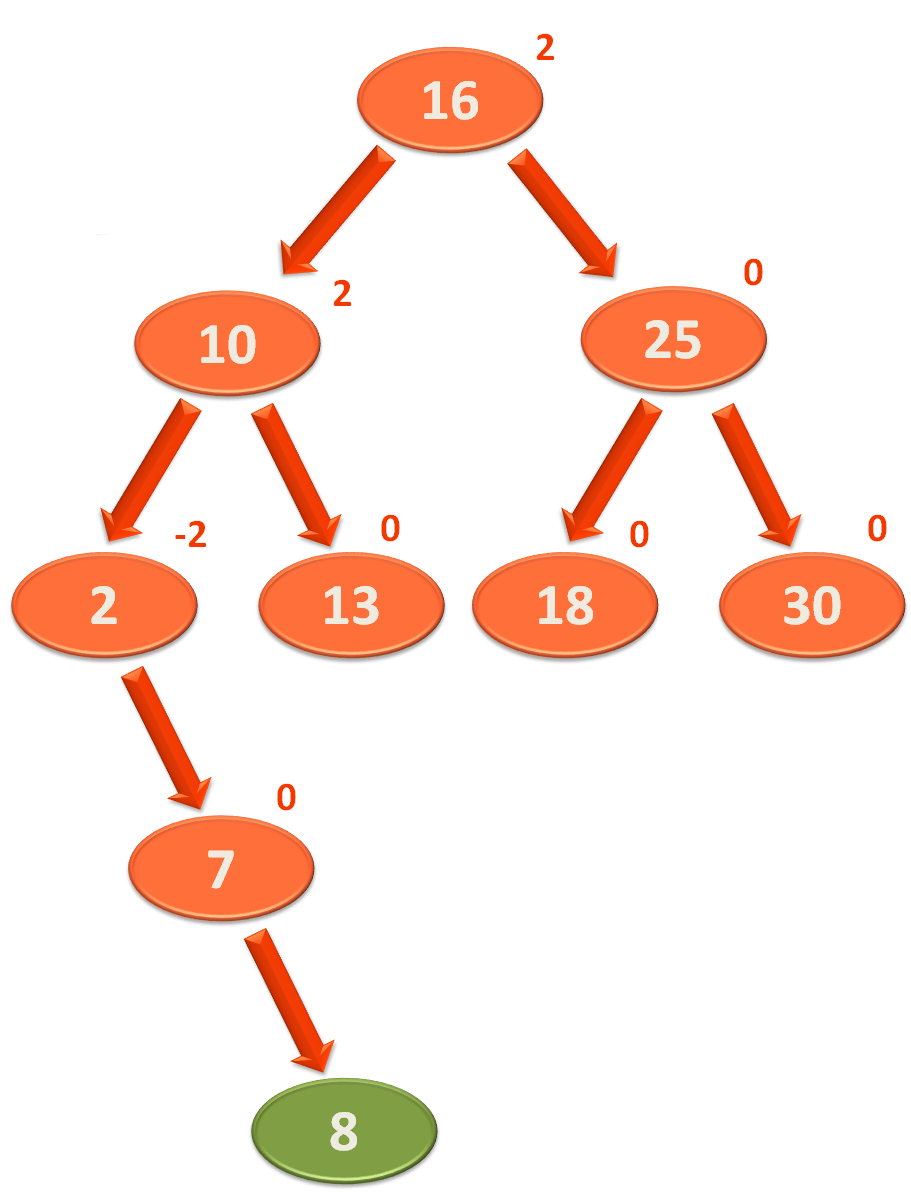
And as we can see, we got a Balance Factor of 2 and -2. Which suggests the Binary Search Tree is Un-Balanced.
Well! We have to balance it now.
So, we take the elements,
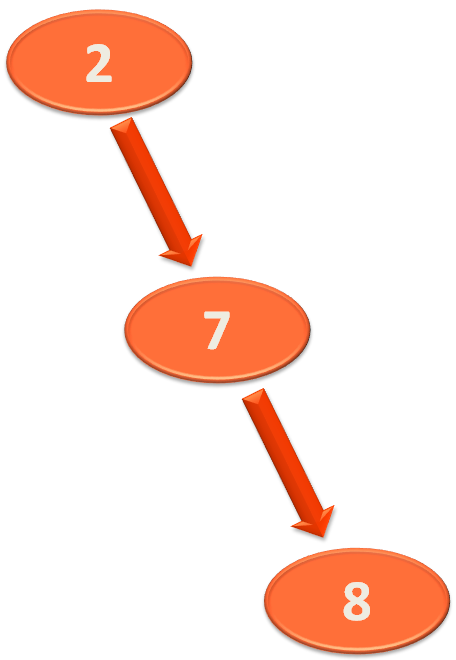
And perform a Left Rotation.

So if we see the entire tree with Balance Factor,
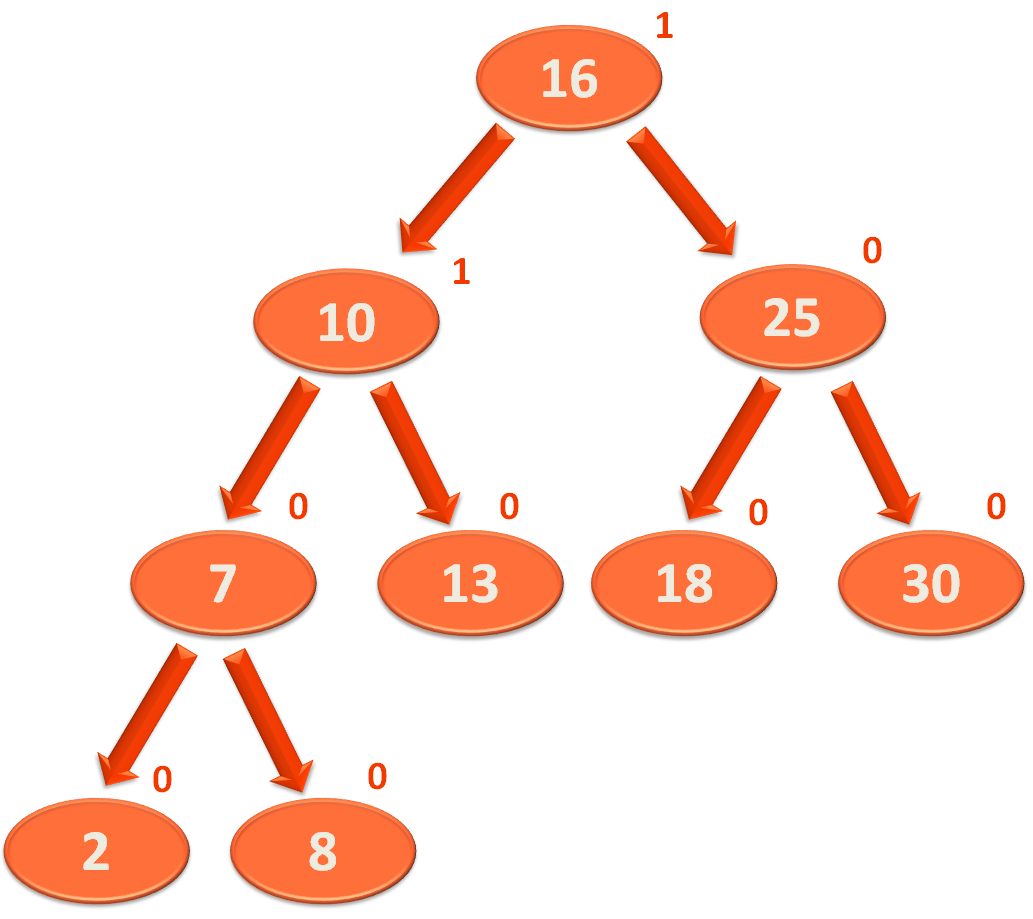
And we could see that the above Binary Search Tree is balanced.
Next, let us see how can we delete an element from an AVL tree.
So, let us take the same Binary Search Tree, with the Balance Factor for each Nodes.
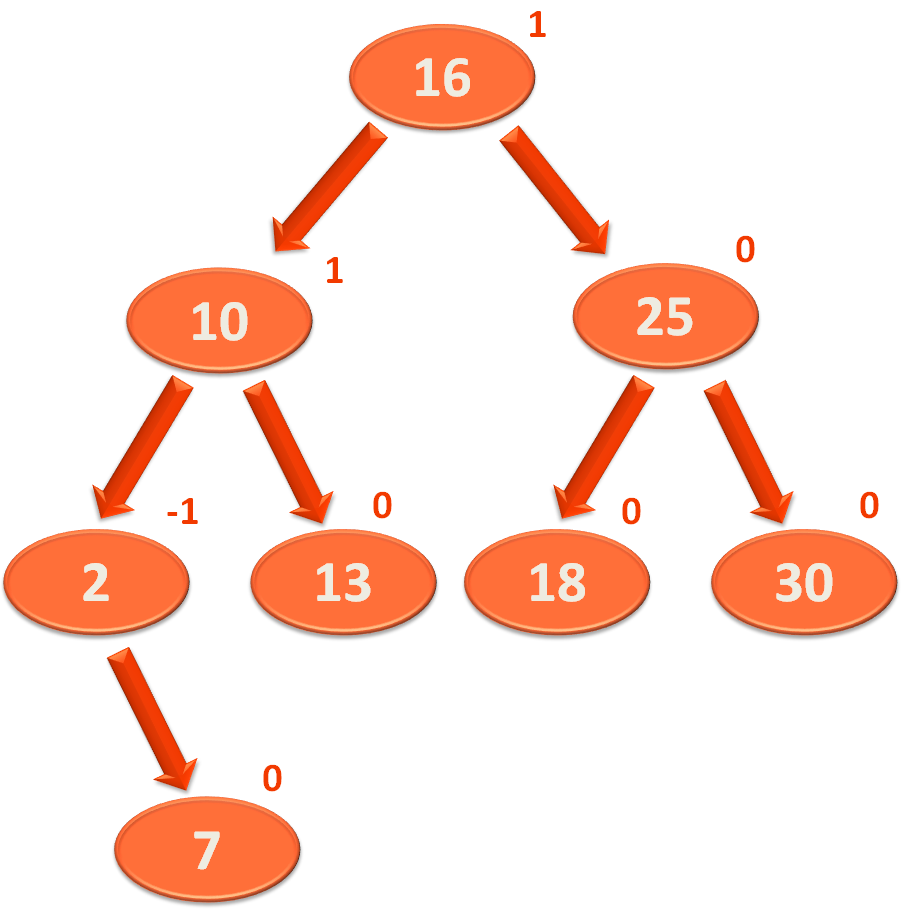
So, the above Binary Search Tree can be said to be balanced as the Balance Factor are either -1, 0 or 1 for all the Nodes.
Now, let us say that we want to delete the element '10' into the above Binary Search Tree.

So, as per the rule of deletion of an element from a Binary Search Tree, we will delete the element '10'.
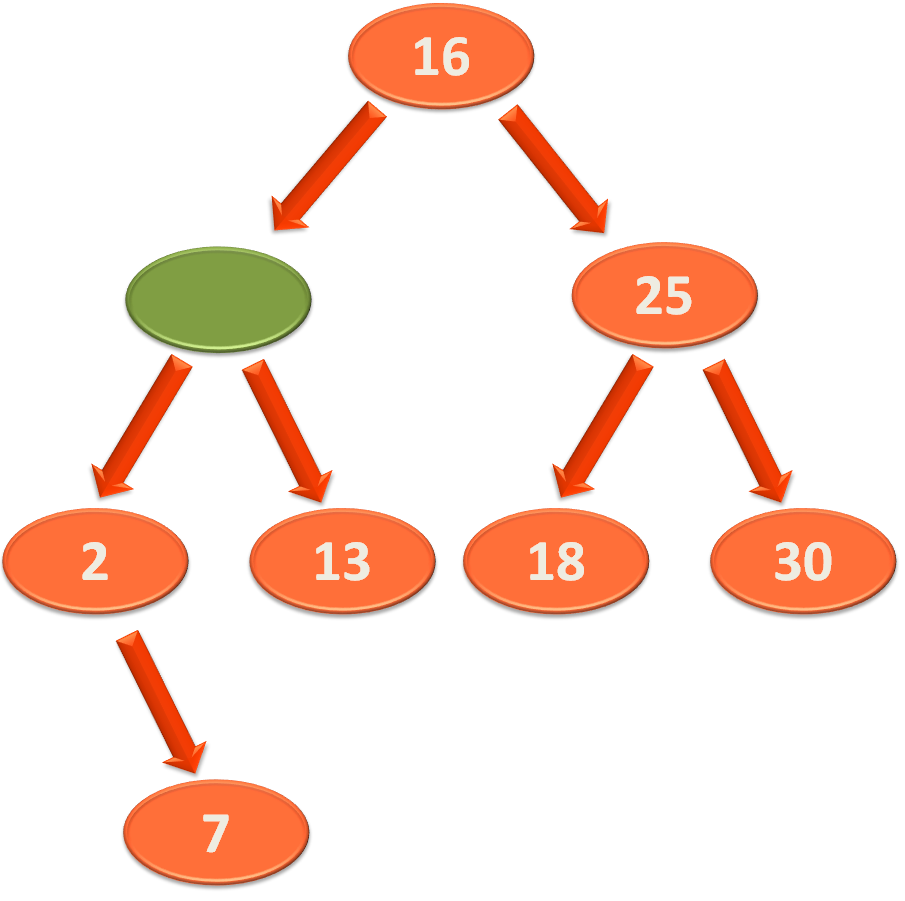
Then replace the empty space of '10' with its right element '13'.
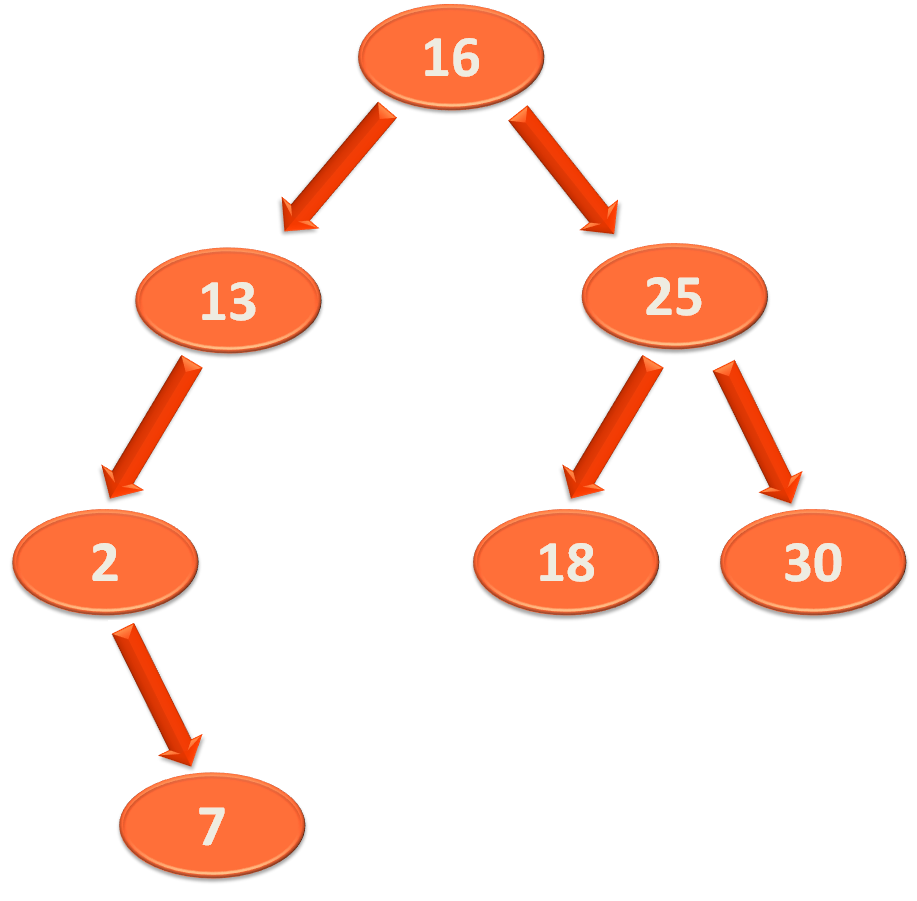
Now, if we calculate the Balance Factor of all the Nodes,
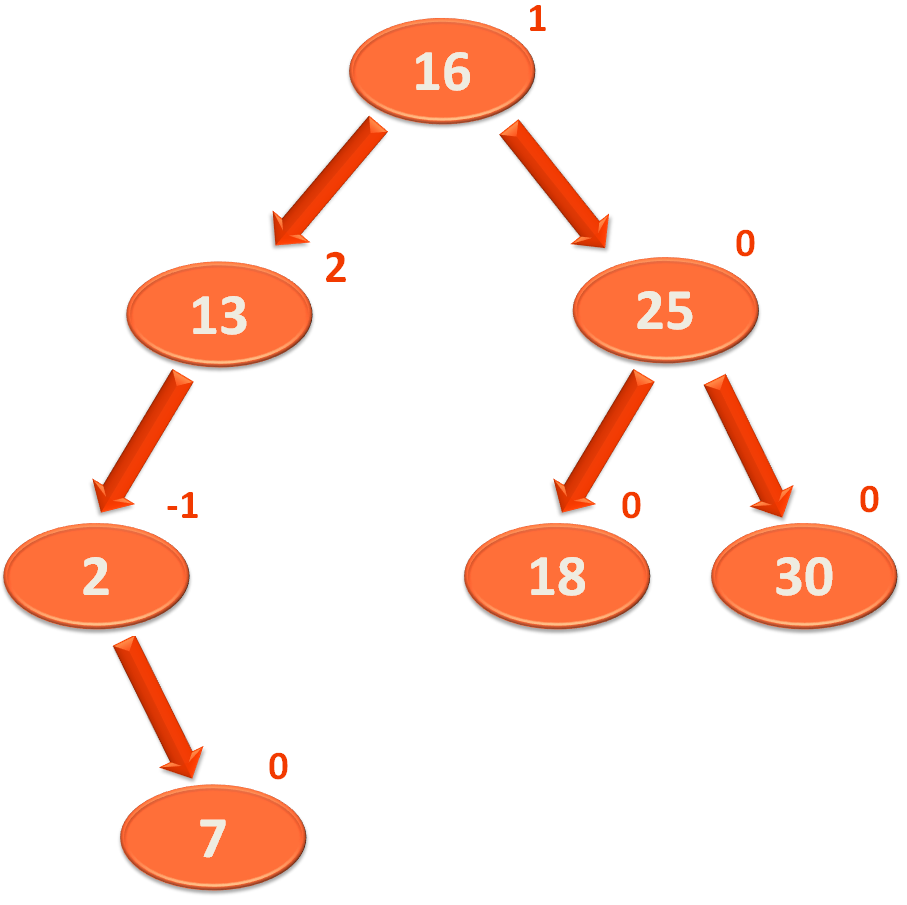
And we can see the Balance Factor became 2 for Node '13'. So, we need to balance the Binary Search Tree.
And we take the elements,

So, we need to perform a left-right rotation.
And we perform a left rotation on the elements '2' and '7' first.

Then perform a right rotation.

And if we see the entire Binary Search Tree with Balance Factor.

And we can see that the Binary Search Tree is balanced.