

There are two approches to Code Binary Search :
At first let us see the Iterative approach :
class BinarySearch {
int search(int arr[], int number) {
int left = 0, right = arr.length-1;
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}
return -1;
}
public static void main(String args[]) {
BinarySearch binarySearch = new BinarySearch();
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };
int num = 5; // Number to be searched.
int index = binarySearch.search(arr, num);
if (index == -1)
System.out.println("Element is not present in the array");
else
System.out.println("The element "+num+" is present at location "+index);
}
}
The above code is quite simple.
We will be searching for the number 5.
int num = 5; // Number to be searched.
From the array,
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };Now, we will call the 'search(...)' method. Where the Binary Search logic resides.
int search(int arr[], int number) {
int left = 0, right = arr.length-1;
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}
return -1;
}
So, initially we are assigning the value of the variable 'left' with 0 and 'right' with arr.length-1 (i.e. 8).
int left = 0, right = arr.length-1;

Next, we run a 'while' loop that only stops when 'left' and 'right' variables have crossed each other or we find the element.
In simple words it only stops when 'left' variable is greater than 'right'.
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}
We calculate the 'midpoint'.
int midPoint = (left + right) / 2;
i.e. 4(As we take 4 only from 4.5).
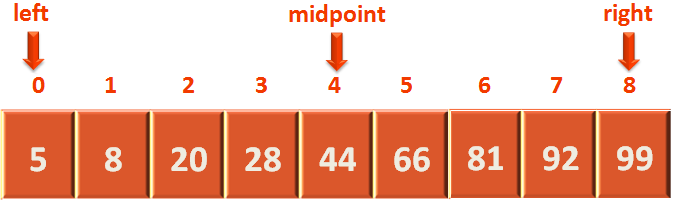
Then we check, if the 'number' to be searched (i.e. 5) is equal to arr[midpoint] or not ?
if (number == arr[midPoint])
return midPoint;In this case, the 'number' to be searched i.e. 5 is not equal to arr[midpoint] i.e. 44.
So, we go to the next 'if' statement. Where we check if the 'number' to be searched is less than arr[midpoint] or not ?
if (number < arr[midPoint])
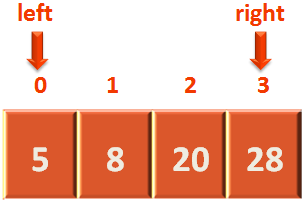
right = midPoint;In this case the 'number' to be searched i.e. 5 is less than arr[midpoint] i.e. 44.
So, we make the 'right' variable point to a position, just before the 'midpoint' was pointing to.
And discard the right part along with the 'midpoint'.
right = midPoint-1;
And the while loop repeats again.
Calculating the 'midpoint'.

And the same process repeats until we find the element.

Now, we find the element.
if (number == arr[midPoint])
return midPoint;And the loop ends returning 'midpoint'.
And we get the index, where the element 5 resides.
int index = binarySearch.search(arr, num);
Finally, we print the index, where the element 5 is present.
System.out.println("The element "+num+" is present at location "+index);And, what if the element we are searching is not present in the array?
Say, we are trying to search for the element 4, which is not in the array.
In that case 'left' and 'right' crosses each other and index is returned as -1.
return -1;
And we print the below statement.
if (index == -1)
System.out.println("Element is not present in the array"); Next, let us look at the recursive approach.
Recursion is a process, where a method calls itself. There are some recursive algorithms that are a little tough to understand.
But, trust me, the Recursive approach of Binary Search is very easy to understand.
class BinarySearch {
int search(int arr[], int left, int right, int number) {
if (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
return search(arr, left, midPoint-1, number);
else
return search(arr, midPoint+1, right, number);
}
return -1;
}
public static void main(String args[]) {
BinarySearch binarySearch = new BinarySearch();
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };
int len = arr.length-1;
int num = 5;
int index = binarySearch.search(arr, 0, len , num);
if (index == -1)
System.out.println("Element is not present in the array");
else
System.out.println("The element "+num+" is present at location "+index);
}
}
The above recursive code is almost same as the Iterative approach, with a mild difference.
Let us just understand the difference.
Below is the only piece of code that is different from the Iterative code.
if (number < arr[midPoint])
return search(arr, left, midPoint-1, number);
else
return search(arr, midPoint+1, right, number);Let us take the iterative piece and compare it.
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;In the iterative piece we have made
right = midpoint-1;
If the number to be searched is less than the 'midpoint'.
We have exactly done the same thing in recursive approach as well.
if (number < arr[midPoint])
return search(arr, left, midPoint-1, number);If the number to be searched is less than the 'midpoint'. We make a recursive call to the method :
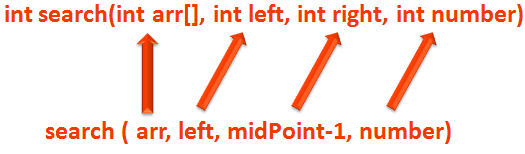
Which means, the 'int search(int arr[], int left, int right, int number)' method is called again with the new value of 'right' as 'midPoint-1'.
Which is exactly same as the Iterative piece.
right = midpoint-1;
Similarly, in the 'else' part of Recursive code, we have,
else
return search(arr, midPoint+1, right, number);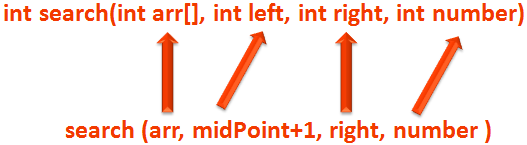
Which is exactly same as the Iterative piece.
left = midPoint+1;
We have claimed that the running time for Binary search is O(log n).
How do we calculate log n?
There are 9 elements in the above array. For a clean and easy calculation let us consider the above array has 8 elements.
We know 8 can also be represented as (2)3.
Now, we can say,
And,
8 = (2) 3 is exactly equivalent to also be represented as log28 = 3.
Now since, we have considered the above array has 8 elements. Which has a running time of log 3.
Let's prove it :
So, Binary Search ran 3 times. And thats all we had to prove.
Running time of Binary Search : O(log n)