There are two approches to Code Binary Search :
At first let us see the Iterative approach :
#include <iostream>
using namespace std;
class BinarySearch {
public :
int search(int arr[], int number, int size) {
int left = 0;
int right = size-1;
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}
return -1;
}
};
int main() {
BinarySearch binarySearch;
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };
int size = sizeof(arr) / sizeof(arr[0]);
int num = 5; // Number to be searched.
int index = binarySearch.search(arr, num, size);
if (index == -1)
cout << "Element is not present in the array";
else
cout << "The element " << num << " is present at location " << index;
}
The above code is quite simple.
We will be searching for the number 5.
int num = 5; // Number to be searched.
From the array,
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };Now, we will call the search(...) method. Where the Binary Search logic resides.
int search(int arr[], int number) {
int left = 0;
int right = size-1;
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}
return -1;
}So, initially we are assigning the value of the variable left with 0 and right with size-1 (i.e. 8).
int left = 0; int right = size-1;
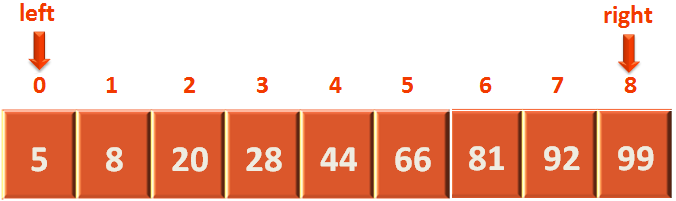
Next, we run a while loop that only stops when left and right variables have crossed each other or we find the element.
In simple words it only stops when left variable is greater than right.
while (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
right = midPoint-1;
else
left = midPoint+1;
}We calculate the midpoint.
int midPoint = (left + right) / 2;
i.e. 4(As we take 4 only from 4.5).
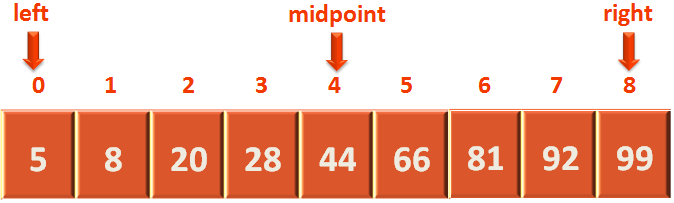
Then we check, if the number to be searched (i.e. 5) is equal to arr[midpoint] or not?
if (number == arr[midPoint]) return midPoint;
In this case, the number to be searched i.e. 5 is not equal to arr[midpoint] i.e. 44.
So, we go to the next if statement. Where we check if the number to be searched is less than arr[midpoint] or not?
if (number < arr[midPoint]) right = midPoint;
In this case the number to be searched i.e. 5 is less than arr[midpoint] i.e. 44.
So, we make the right variable point to a position, just before the midpoint was pointing to.
And discard the right part along with the midpoint.
right = midPoint-1;
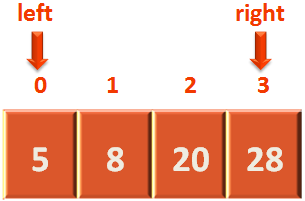
And the while loop repeats again.
Calculating the midpoint.
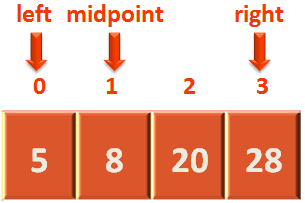
And the same process repeats until we find the element.

Now, we find the element.
if (number == arr[midPoint]) return midPoint;
And the loop ends returning midpoint.
And we get the index, where the element 5 resides.
int index = binarySearch.search(arr, num);
Finally, we print the index, where the element 5 is present.
cout << "The element " << num << " is present at location " << index;
And, what if the element we are searching is not present in the array?
Say, we are trying to search for the element 4, which is not in the array.
In that case left and right crosses each other and index is returned as -1.
return -1;
And we print the below statement.
if (index == -1) cout << "Element is not present in the array";
Next, let us look at the recursive approach.
Recursion is a process, where a method calls itself. There are some recursive algorithms that are a little tough to understand.
But, trust me, the Recursive approach of Binary Search is very easy to understand.
#include <iostream>
using namespace std;
class BinarySearch {
public :
int search(int arr[], int left, int right, int number) {
if (left <= right) {
int midPoint = (left + right) / 2;
if (number == arr[midPoint])
return midPoint;
if (number < arr[midPoint])
return search(arr, left, midPoint-1, number);
else
return search(arr, midPoint+1, right, number);
}
return -1;
}
};
int main() {
BinarySearch binarySearch;
int arr[] = { 5, 8, 20, 28, 44, 66, 81, 92, 99 };
int size = sizeof(arr) / sizeof(arr[0]);
int len = size-1;
int num = 5;
int index = binarySearch.search(arr, 0, len , num);
if (index == -1)
cout << "Element is not present in the array";
else
cout << "The element " << num << " is present at location " << index;
}
The above recursive code is almost same as the Iterative approach, with a mild difference.
Let us just understand the difference.
Below is the only piece of code that is different from the Iterative code.
if (number < arr[midPoint]) return search(arr, left, midPoint-1, number); else return search(arr, midPoint+1, right, number);
Let us take the iterative piece and compare it.
if (number < arr[midPoint]) right = midPoint-1; else left = midPoint+1;
In the iterative piece we have made
right = midpoint-1;
If the number to be searched is less than the midpoint.
We have exactly done the same thing in recursive approach as well.
if (number < arr[midPoint]) return search(arr, left, midPoint-1, number);
If the number to be searched is less than the midpoint. We make a recursive call to the method :
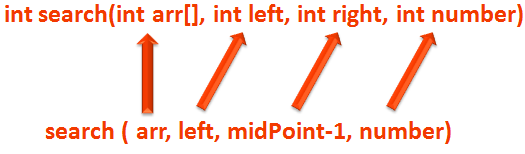
Which means, the int search(int arr[], int left, int right, int number) method is called again with the new value of right as midPoint-1.
Which is exactly same as the Iterative piece.
right = midpoint-1;
Similarly, in the else part of Recursive code, we have,
else return search(arr, midPoint+1, right, number);
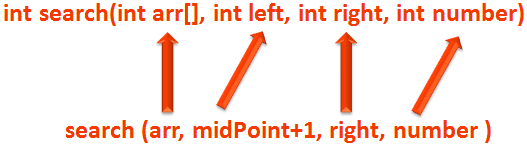
Which is exactly same as the Iterative piece.
left = midPoint+1;
We have claimed that the running time for Binary search is O(log n).
How do we calculate log n?
There are 9 elements in the above array. For a clean and easy calculation let us consider the above array has 8 elements.
We know 8 can also be represented as (2)3 .
Now, we can say,
8 = (2)3
And,
8 = (2)3 is exactly equivalent to also be represented as log2 8 = 3.
Now since, we have considered the above array has 8 elements. Which has a running time of log 3.
Let's prove it:
So, Binary Search ran 3 times. And thats all we had to prove.
Running time of Binary Search : O(log n)