HEAP

And the Edges represents the bus names that travels through that edge/road.

What is a Binary Tree ?

A Tree that can have at-most two children.

Example :

What is a Heap or a Binary Heap ?

A Heap or a Binary Heap is a Binary Tree, where all the elements in the child Node should be greater than its parent. That's a Min Heap(Max Heap should be just the opposite).

So, by definition, a Heap or a Binary Heap is a Binary Tree that has priority elements in its child Nodes. It can also be called as a Min Heap.

We can consider, 'priority elements' as the elements that are greater than the lower priority elements.

Say '7' has a higher priority, when compared to '5'.

Let us simplify it with the below example :

As mentioned above, A Heap or a Binary Heap is a Binary Tree that has priority elements in its child Nodes.

Note :In the entire tutorial, we will be describing Min Heap.

i.e. All the elements in the child Node should be greater than its parent.

Let us take the parent element in Level 1 (i.e. 2). It has two elements in its child Nodes(i.e. 4 and 9). And both 4 and 9 are greater than its parent element i.e. 2.

Similarly, if we take the the elements of Level 2 and Level 3. 10 and 14 are Children of 4. And 17 and 16 are children of 9. Both 10 and 14 are greater than 4 and 17 and 16 are greaterthan 9.

Same applies for Level 3 and Level 4.

The next property of a Heap is that all the levels should be full except the last level that has to be left filled.

Let's make it simple.

Level 1 can have a maximum of one element. Which it has (i.e. 2)

Similarly, Level 2 can have a maximum of two elements. Which it has (i.e. 4 and 9).

Also, Level 3 can have a maximum of four elements. Which it has (i.e. 10, 14, 17 and 16).

Now, Level 4 can have a maximum of eight elements. But there are just five. And all the five elements are left aligned.

And that's the second property. All the levels must be filled, except the last level that should be left aligned.

Examples of trees that are NOT HEAPS

The above tree is not a heap because it doesn't satisfy the second condition. i.e. The last level has to be left filled. As in level 4, 25 should be the left child of 17. But, instead it is the right child of 17 and the left child is empty.

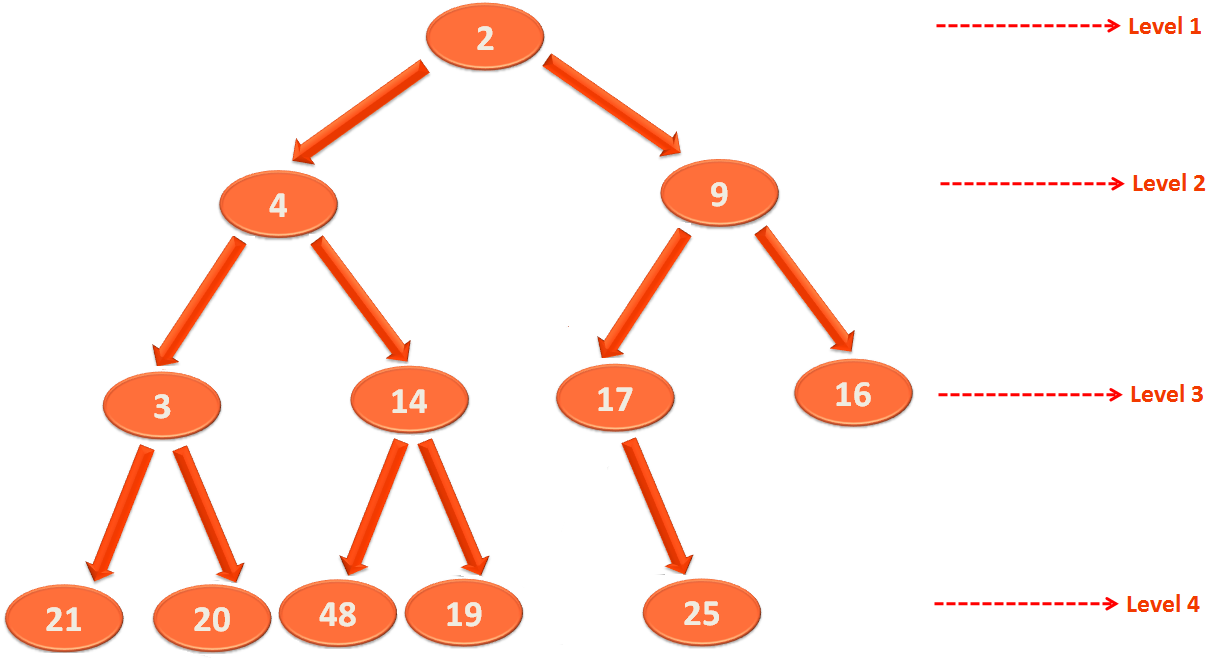
Look closely, the above tree is not a Heap. Why?

Take a look at Level 2 and Level 3. '4' from Level 2 has a left child '3'. But that shouldn't be. As the child should be greater than parent.

Which violates property 1. i.e. All the elements in the child Node should be greater than its parent.

How to find the minimum element of a Heap?

The minimum element of the Heap will always be the root element or the element at Level 1.

Because if the minimum element would be anywhere else in the Heap. It would violate the property, "All the elements in the child Node should be greater than its parent".

Finding the minimum element would take O(1) time. As we now where it lies.

What is the Height of a Heap ?

If we look at the above Heap, we can see that the height of the Heap is 4 (Since it has 4 levels).

And it has 12 elements in it. And the above Heap can have a max of 16 elements.

Now, if we try 'log 16', we get 4. Which is the height of the Heap.

So, if there are 'n' elements in a Heap. The height of a Heap would be,

h = log n

Implementing Heaps using Arrays

To implement a Heap using Arrays, we will start filling the array starting from the root element of the Heap. Or the elements from Level 1.

Then we will start moving one level down and fill elements from left to right.

Let me clear it.

At first we will take the root element(i.e. 2) from Level 1 and place it in the 1st position of the array.

Similarly, we take the elements from level 2. And place the elements starting from the leftmost element of level 2. i.e. We take 4 and place it in the second location of the array.

And take 9 and place at the 3rd position in the array.

Same way, we will take the elements of Level 3. And place the elements starting from the leftmost element of level 3. i.e. We will start from 10, then 14 and so on.

And we do the same for level 4.

Now, since the Array is filled. Let us try to see the logic to find the elements.

To find the Parent of an element in the above array

The logic is

parent = (i-1)/2 (Where 'i' is the position of the element in the array)

Let us pick a random element from the array. Say 14.

Now, 14 is in location 4 of the array.

Now,

parent = (4-1)/2 = 1.5 = 1 (Let us ignore the decimal value)

So the parent of 14 is in location 1 in the array, i.e. 4.

And if we look at the Heap. 4 is the parent of 14.

To find the Left child of an element in the above array

The logic is

left = (2*i)+1 (Where 'i' is the position of the element in the array)

Let us pick a random element from the array. Say 9.

Now, 9 is in location 2 of the array.

Now,

left = (2*2)+1 = 5

So the left child of 9 is in location 5 in the array, i.e. 17.

And if we look at the Heap. The left child of 9 is 17.

To find the Right child of an element in the above array

The logic is

right = (2*i)+2 (Where 'i' is the position of the element in the array)

Let us pick a random element from the array. Say 14.

Now, 14 is in location 4 of the array.

Now,

right = (2*4)+2 = 10

So the right child of 14 is in location 10 in the array, i.e. 19.

And if we look at the Heap. The right child of 14 is 19.

Note : So, we can say the children of Node i are (2*i)+1 and (2*i)+2.

Insertion in a Heap

Let us take the below Heap :

Now, we will insert a new element 5 in the Heap.

And as per the second property of Heap, all the elements in the last level should be left filled.

So, we can insert 5 as the right child of 17.

Now, according to the first property, the new element i.e. 5 should be greater than its parent i.e. 17.

But we can see 5 is less than its parent 17. S0, we swap the positions of 5 and 17.

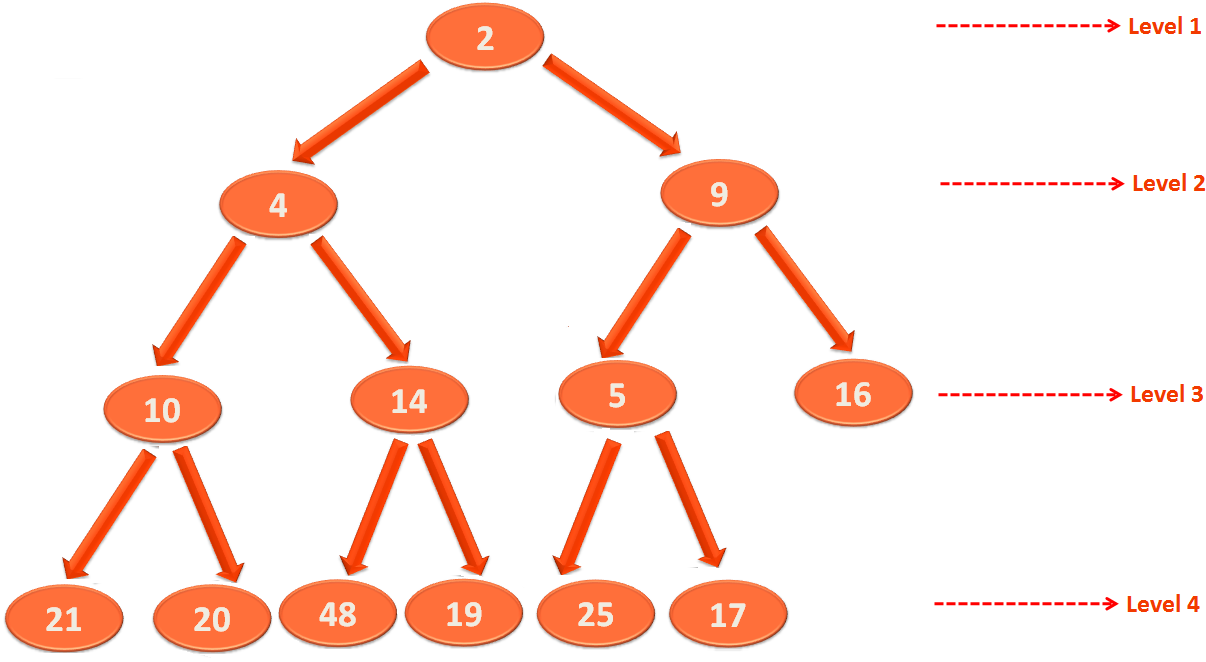
Now, we can see that the parent of 5 is 9. Which is violating the 1st property.

So, we swap 5 and 9.

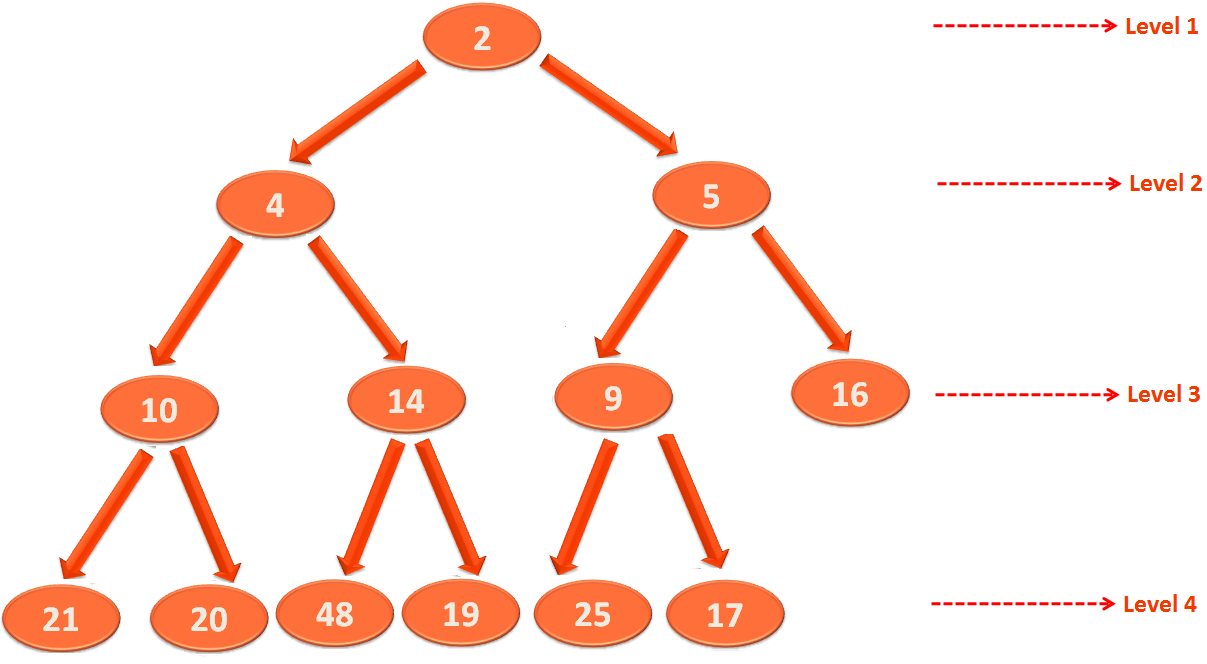
Now, if we compare 5 with its parent i.e. 2. We can see 5 is greater than 2.

So, 5 is in the right place.

What should be the time taken to insert an element in the Heap ?

We have seen in the above scenario that in the worst case, the element needs to travel all the way up.

Just note, in the above case the Heap has 4 levels and the new element had to travel till Level 2. If the element would have been 1, it would have to travel to level 1.

So, in the worst case the element had to travel till the top. Which is the height of the Heap.

And we have seen, it takes O(log n) time to find the height of the Heap.

So, the insertion of an element in a Heap takes O(log n) time.

Heapify

As the name suggests, Heapify is a method that is used to convert a non-heap to a heap. The only condition should be, both the children of the node where Heapify needs to be applied, should be a Heap.

Let me clarify with an example,

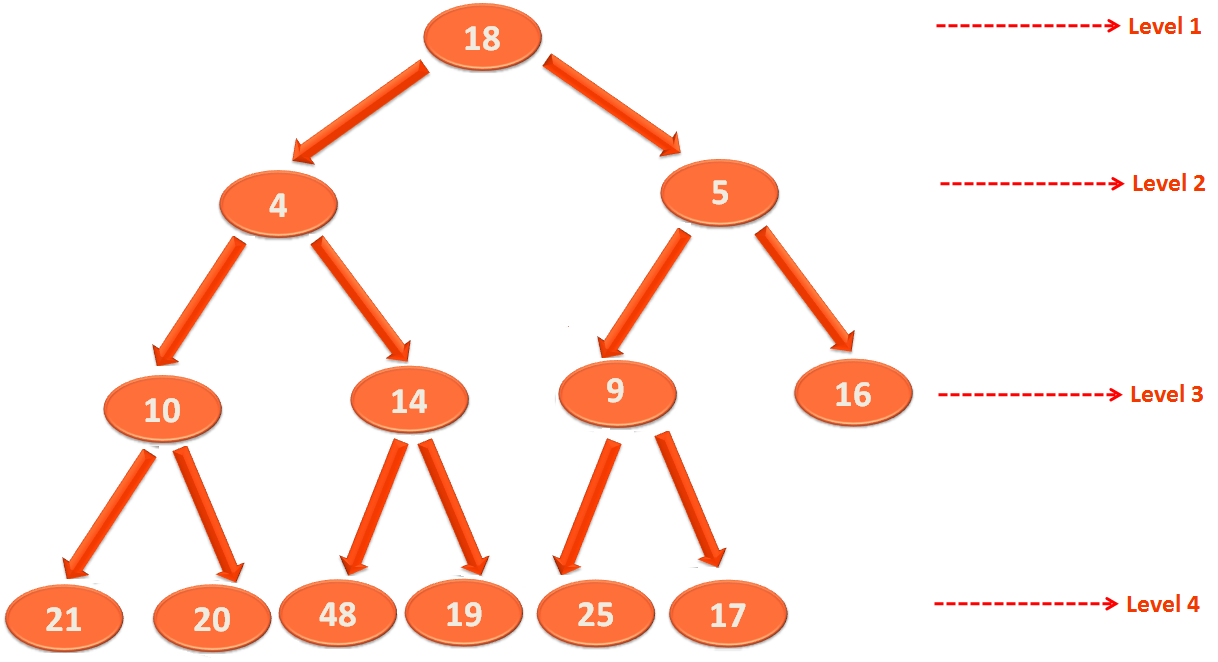
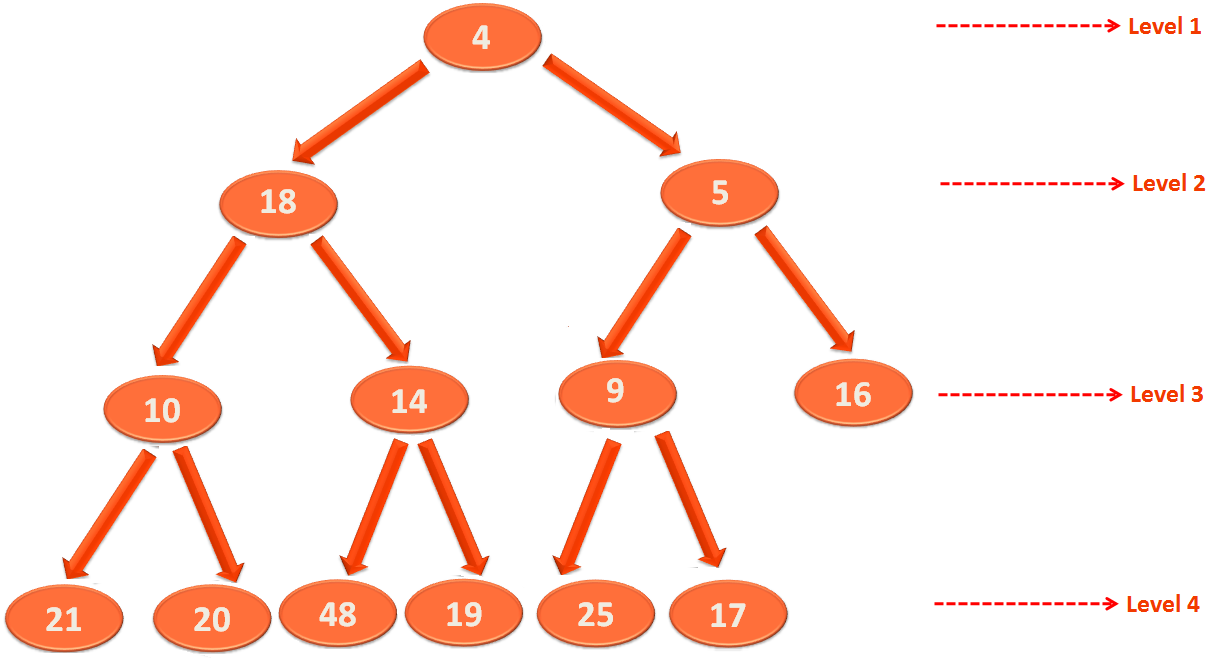
As we can see in the above case, the root element at level 1 is 18. That is greater than both of its children i.e. 4 and 5. So, it violates the heap property.

In this case, we can apply Heapify on 18. But the only condition should be, both the children of 18 should be a Heap.

Now, if we check the children of 4. They are 10 and 14. Both are greater than 4. Similarly, the children of 10 are 21 and 20. And the children of 14 are 48 and 19. Both satisfy the Heap structural property.

Again, if we check the children of 5. Its 9 and 16. Both are greater than 5. And if we check the children of 9, they are 25 ad 17. Both are greater than 9.

So, we can conclude saying the children of 18 are Heaps and we can apply Heapify on 18.

Now, the Heapify method works in the following way :

It checks, who among its children are smaller. i.e. The children of 18 are 4 and 5. And 4 is smaller than 5.

So, Heapify swaps 4 with 18.

So , 18 is the left child of 4 . Now , Heapify checks if 18 is in the right position. But it isn't, as 18 is greater than its children 10 and 14 .

So , Heapify checks who among its children are smaller. And it finds 10 is smaller than 14 .

So , Heapify swaps 18 and 10 .

Again the Heapify method checks, if the children of 18, i.e. 21 and 20 is greater than 18 or not. And in this case it satisfies the heap property.

Running time of Heapify

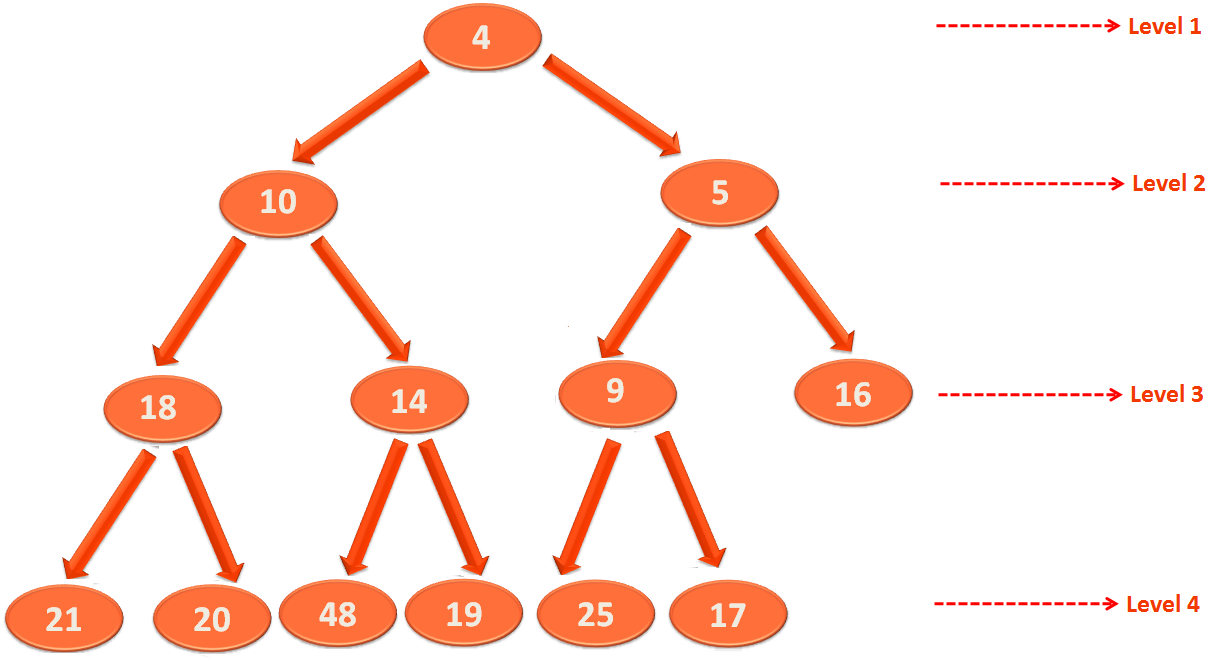
We have seen the running time to insert an element in the Heap is O(log n). As it travels up the heap .

And in case of Heapify , the element travels down the Heap . That should be equivalent to the height of the Heap.

Running time of Heapify : O(log n)

Deletion of the minimum element in a Heap

We have seen that the minimum element or the smallest element always stays on top of the Heap.

Now, if we remove the root element and rearrange the Heap, we are done.

Let us see the steps with the below example :

We remove the root element 2 (Which is the smallest element) from Level 1.

Next, take the rightmost element from the last level or level 4(i.e. 17). And place it in Level 1, in place of 2.

Now, the element 17 is on the top level, but it doesn't satisfy the Heap property(As it is greater than its children).

But the exiting thing to note is, the children of 17, i.e. 4 and 5 are Heaps.

And we can Apply Heapify in Level 1.

After applying Heapify, 17 has gone, all the way down to Level 3.

And is a Heap now.

Running time to remove the minimum element from Heap

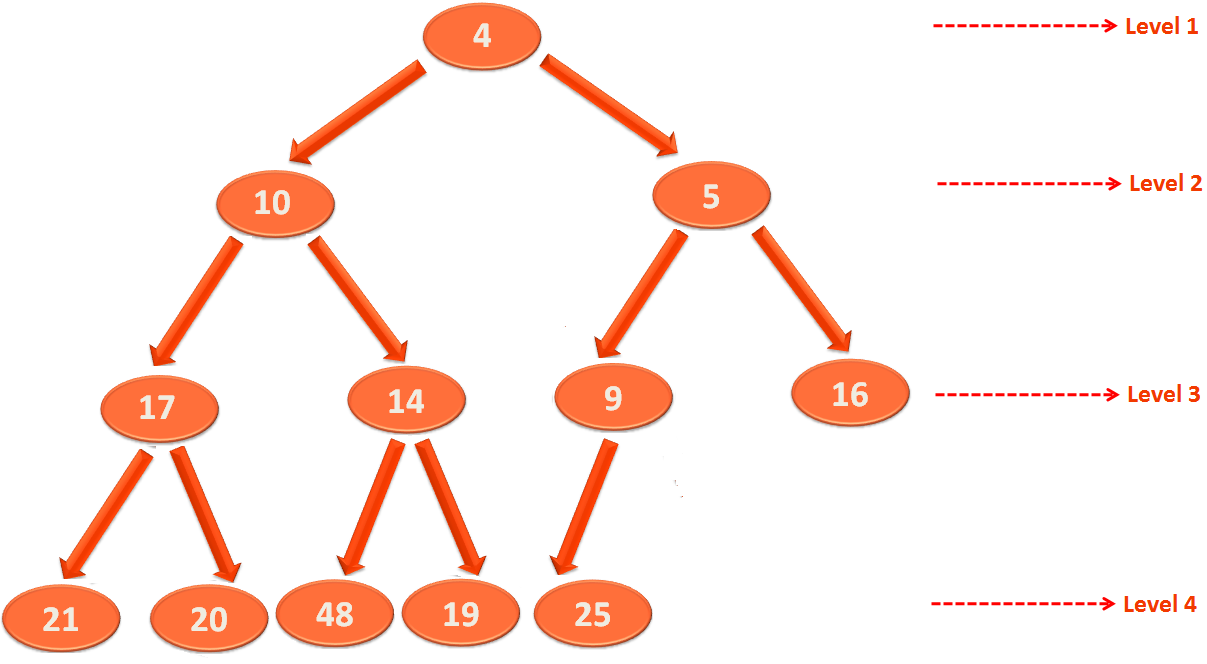
To remove the root element from Level 1 and place the rightmost element from Level 4 takes constant time.

And Heapify takes O(log n).

Time taken to remove minmm element from Heap : O(log n)

Building/Creating a Heap

Say, we are given a few numbers. And we need to create a Heap out of it.

What we will do is, create a tree out of the given numbers and then use Heapify to create a Heap out of it.

Let's us explain with the below example :

We are given a list of 6 numbers,

4, 78, 32, 2, 45, 11

Now, we will follow the below steps to create a Heap out of it :

We will form a binary tree with the following numbers.

What we have done is, taken the first element 4 and placed it in the root element(In Level 1). Then we have taken the second and third element 78 and 32 and placed it as left and right child of the root element(In Level 2).

And, similarly Level 3 is filled.

Next, we will use Heapify to transform the above binary tree to a Heap.

Now, the condition of Heapify is, the children of the Node on which Heapify is applied, must be a Heap.

So, let us take the last Level(i.e. Level 3). Now, since there are no children of the elements of Level 3(i.e. 2, 45 and 11). We can consider 2, 45 and 11 satisfies the property of Heap.

Now, let us come to Level 2. We can apply Heapify on 78(As both of its children 2 and 45) can be considered as Heap.

After applying Heapify on 78, we get,

Similarly, we will apply Heapify on 32 of Level 2. And get the below result.

Now, we can apply Heapify on the root element i.e.4. As both of its children 2 and 11 are Heaps.

After applying Heapify, we get,

And finally we get a Heap.

Running time to build a Heap

Running time to build a heap is : O(n)

❮❮ PREV NEXT ❯❯