

Just like Merge Sort, the coding for Quick sort is also based on Recursion. If you don't know recursion, no worries. We will explain Recursion as much as possible.
package main
import "fmt"
func sort(arr []int,left int , right int) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
// right part.
pos := divide(arr, left, right)
sort(arr, left, pos) // Sorts the left part of the array recursively.
sort(arr, pos+1, right) // Sorts the right part of the array recursively.
}
}
func divide(arr []int, low int, high int) int {
pivot := arr[low]
j := high;
i := low;
for true {
for arr[j] > pivot {
j--
}
for arr[i] < pivot {
i++
}
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}
}
return 0
}
func main() {
arr := []int{7,5,8,6}
fmt.Println("Array before Sorting")
for _, val := range arr {
fmt.Println(val)
}
fmt.Println()
sort(arr, 0, len(arr)-1)
fmt.Println("Array after Sorting");
for _, val := range arr {
fmt.Println(val)
}
}
In the above code we have two methods:
func sort(arr []int,left int , right int)
and
func divide(arr []int, low int, high int) int
The first method sort(...) divides the Array into two or more parts.
And the next method divide(...) returns the position, based on what the Array is divided. It calculates the position such that, all the elements less than the pivot element is placed on the left side of the divided Array and all the elements greater than or equal to the pivot element is placed on the right side of the divided Array.
The execution begins from the main(..) method.
So, initially we will be taking the array,
arr := []int{7,5,8,6}And pass it to the sort(...) method,
sort(arr, 0, len(arr)-1)
func sort(arr []int,left int , right int) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
// right part.
pos := divide(arr, left, right)
sort(arr, left, pos) // Sorts the left part of the array recursively.
sort(arr, pos+1, right) // Sorts the right part of the array recursively.
}
}So, we are passing the array arr, its starting point i.e. 0(mentioned left inside the parameter of sort(...) method) and the end point i.e. arr.length-1 (mentioned right inside the parameter of sort(...) method).
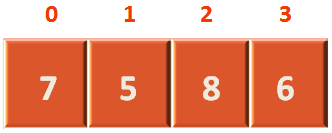
The array arr contains (7, 5, 8, 6).
And the value of the variable, left is 0.
The length of the array is 4. Which means (4-1), i.e. 3. So, the value of the variable right is 3.
In the next step we check
if(left < right)
Which means the array length should be more than 1(i.e. If the array length is not more than 1, there is just one element in the array and no further calculation is needed).
Then we calculate the position of pivot element by calling the divide(arr, left, mid) method, so that we can divide the array into two parts.
int pos = divide(arr, left, mid);
Since, our idea is to move the pivot element at position in the array, such that all the elements smaller to the pivot element would be placed at the left of it.
And all the elements greater than the pivot element should be placed at the right hand side of the pivot element.
And that is exactly the work, divide(int arr[], int low, int high) is going to do.
It places the pivot element at the right position and returns the exact position of the pivot element.
func divide(arr []int, low int, high int) int {
pivot := arr[low]
j := high;
i := low;
for true {
for arr[j] > pivot {
j--
}
for arr[i] < pivot {
i++
}
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}
}
return 0
}All we are doing in the above case is,
func divide(arr []int, low int, high int) int
Getting the elements of the array in arr[].
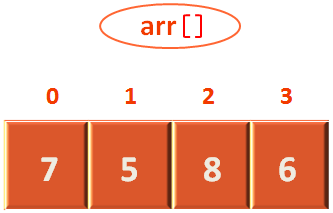
And the low and high variables contains 0 and 3.
In the next step, we get the pivot element(The first element in the array will be the pivot element).
int pivot = arr[low];
Now, since arr[low] or arr[0] contains 7. The pivot variable pivot will have 7.

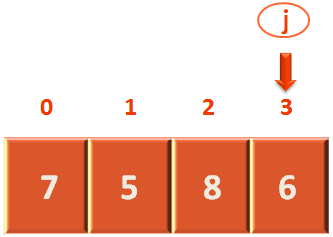
Next, we will make j to point to the last element.
j := high
So, the value of j becomes
j = 3 (Since, high = 3)
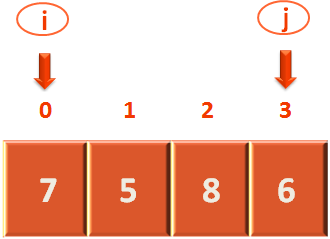
Similarly, we will make i to point to the first element.
i := low
So, the value of i becomes
i = 0 (Since, low = 0)
Now, let's check the main chunk of code from above:
for true {
for arr[j] > pivot {
j--
}
for arr[i] < pivot {
i++
}
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}
}There are three for loops.
for true
for arr[j] > pivot {
j--
}for arr[i] < pivot {
i++
}The outer loop
for true
Only exits when i and j cross each other.
Let us see how.
The for loop runs indefinitely,
for true
And the above for loop only stops when the if condition is not satisfied and the control goes to the else statement,
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}Which means when i is greater than or equal to j, it returns j and exits.
In other words, when i and j cross each other, The above for loop (i.e. for true) stops.
Now, let us come to the inner for loop,
for arr[j] > pivot {
j--
}So, the idea is to move j towards the left until it finds an element less than the pivot element.
And, the above for loop exactly does the same.
It keeps on decrementing j, and the loop continues until it finds an element less than the pivot element.
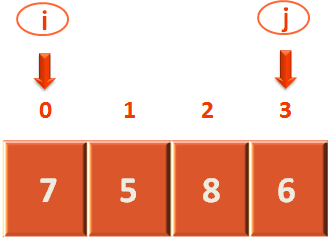
Let us demonstrate in brief,
for arr[j] > pivot {
j--
}for arr[j] > pivot {
j--
}When we replace j and pivot with its actual values,
for arr[3] > 7 {
j--
}In the above case, the value of j is 3, and we compare with the pivot element.
And we can see that arr[3] has 6, i.e. less than the pivot element i.e. 7.
So, the control doesn't gets into the while loop, and j keeps on pointing to the 4th location.
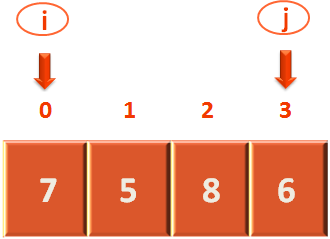
Similarly, let us come to the next inner for loop,
for arr[i] < pivot {
i++
}So, the idea is to move i towards the right until it finds an element less than the pivot element.
Even in this case, the above for loop does the same.
It keeps on incrementing i until it finds an element less than or equal to the pivot element.
Let us demonstrate in brief,
for arr[i] < pivot {
i++
}for arr[i] < pivot {
i++
}When we replace i and pivot with its actual values,
for arr[0] < 7 {
i++
}And we can see that arr[0] has 7, i.e. equal to the pivot element i.e. 7.
So, the control doesn't gets into the for loop, and it keeps on pointing i to the 1st location.
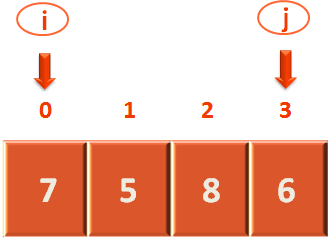
Now, since we are done with the for loops. It's time to check the if block (That helps to exit from the outer loop).
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}The above if block checks, if i and j have crossed each other or not (i.e. Have a look at the above array block. Until i < j, i and j have not crossed each other).
In the above case i is less than j. Since, the value of i is 0 and the value of j is 6.
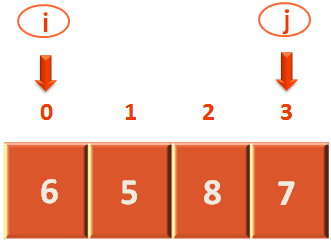
So, we get into the if block. And all it does is swaps the values of arr[i] and arr[j].
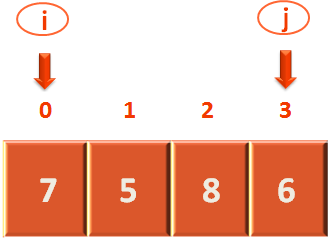
So, we swap the values of arr[0] and arr[3].
And the new array contents after swapping becomes :
We are not yet done as the return statement in the else part has still not executed.
else {
return j
}So, we continue with the outer loop,
for true
And reach the inner for loop,
for arr[j] > pivot {
j--
}And, the idea is to move j towards the left until it finds an element less than or equal to the pivot element.
And, the above for loop exactly does the same.
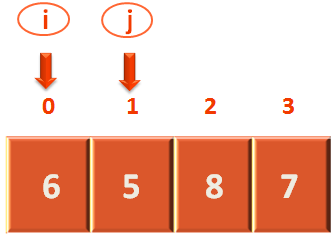
So, after looping through. The for loop stops at the second position(i.e. j) when it finds the element 5 in the second location in the array is less than the pivot element.
Similarly, the control comes to the next while loop dealing with i.
for arr[i] < pivot {
i++
}And, the idea is to move i towards the right until it finds an element greater than or equal to the pivot element.
And, the above for loop exactly does the same.
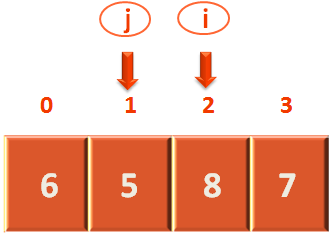
And, after looping through. The for loop stops at the third position when it finds the element 8 in the third location in the array is greater than the pivot element.
And we can see that i and j have crossed each other.
So, if we look at the if statement,
if (i < j) {
temp := arr[j]
arr[j] = arr[i]
arr[i] = temp
} else {
return j
}The value of i is 2 and the value of j is 1.
And finally the control comes to the else statement and returns the value of j i.e. 1.
Now, let us divide the above array based on the value of j.
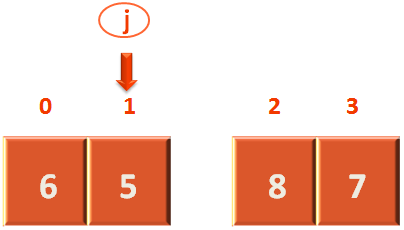
And BINGO ! That's what we wanted. All the elements less than the pivot element i.e. 7 is on the left side. And all the elements greater than or equal to the pivot element i.e. 7 is on the right side.
And the next piece of code will take the above two parts and calculate it further.
Let us see how ?
In the next line, the value of j(i.e. 1) will be assigned to the pos variable.
Let us take a look at the sort(..) method again,
func sort(arr []int,left int , right int) {
if(left < right) {
// Calculates the point based on which the array is divided into left part and
// right part.
pos := divide(arr, left, right)
sort(arr, left, pos) // Sorts the left part of the array recursively.
sort(arr, pos+1, right) // Sorts the right part of the array recursively.
}
}The pos variable, from the above code contains 1 (i.e. The value returned from sort(arr []int,left int , right int))
pos := divide(arr, left, right)
Now, comes the fun part. When we encounter the line,
sort(arr, left, pos)
We call the sort(...) method from the sort(...) method itself. And this is called recursion. Where a method keeps on calling itself until it comes to an end. And it maintains an internal stack which is hidden from the programmer.
It might look a little complex, but trust me it is quite simple. Just stay with me.
All we are doing in this step is, taking the left hand side of the array and passing it to the sort() method.
i.e. If we substitute the values of sort(arr, left, pos)
We can see left variable has 0 and pos variable has 1.
Which means, the sort() method is going to operate on the left side of array.
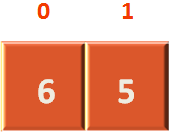
And if we come to the next line,
sort(arr, pos+1, right)
The above line will deal with the right part of the array.
i.e. If we substitute the values of sort(arr, pos+1, right)
We can see pos+1 variable would be 2(Since value of pos variable is 1) and right variable has 3.
Which means, this time the sort() method is going to operate on the right side of array.
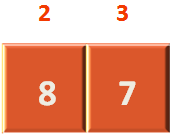
Let us see it in brief, how the array is partitioned at every step :
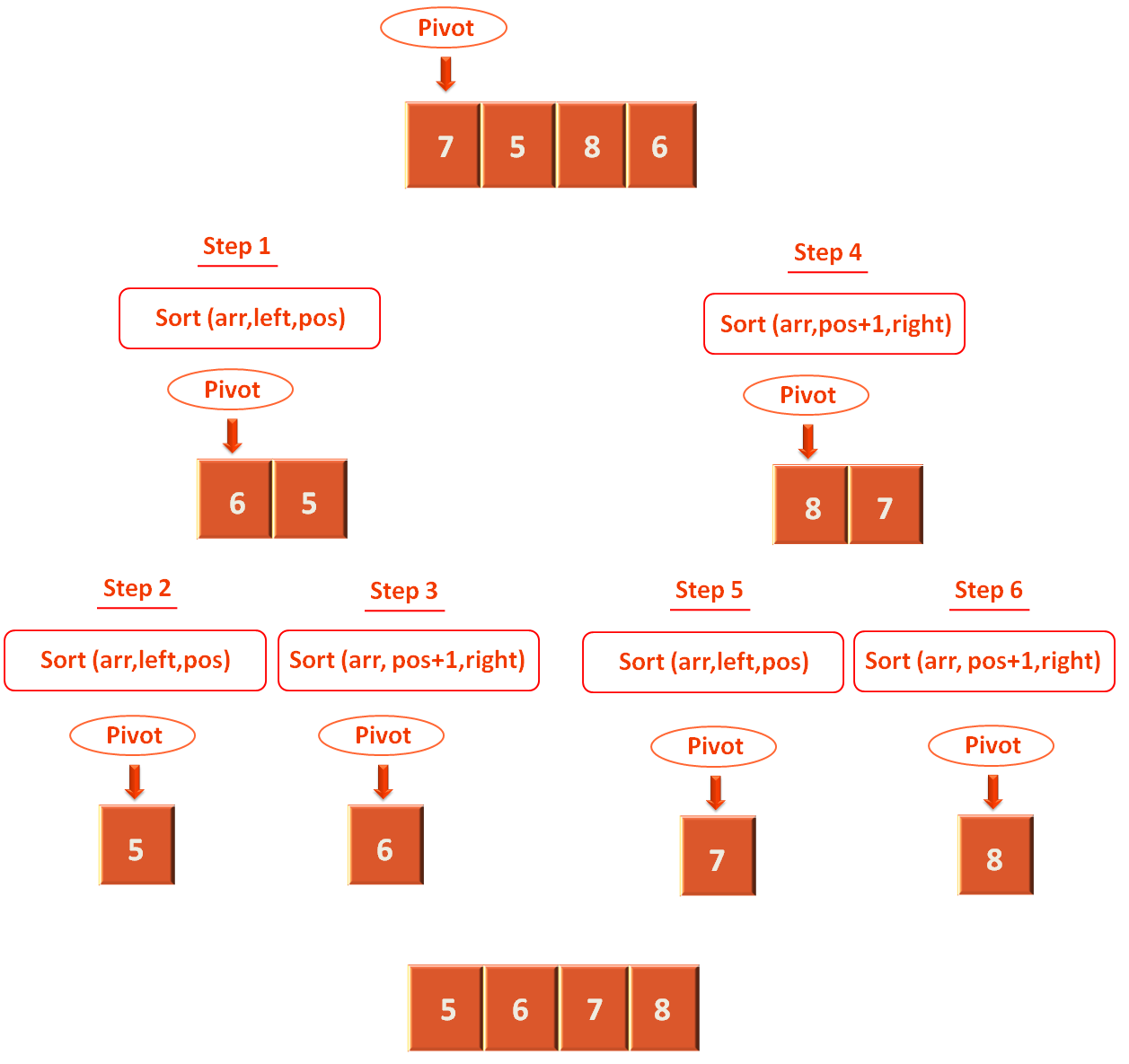
The above 6 step process is the best way to understand the code.
We have the array with values 7, 5, 8, 6.
From which we select the pivot element(i.e. 7) and call the divide(arr, left, right) method. Based on this pivot element, the array is divided into two parts. Such that all the elements less than the pivot element will be placed on the left half and all the elements greater than or equal to the pivot element will be placed on the right part.
if(left < right)
Now, if we combine all the parts. We get a sorted array.
5, 6, 7, 8.
There are complicated processes to understand the efficiency/running for Quick Sort. But we will keep it simple, so that it becomes simple to understand and we can calculate the running time for any algorithm this way.
Let's say we are lucky.
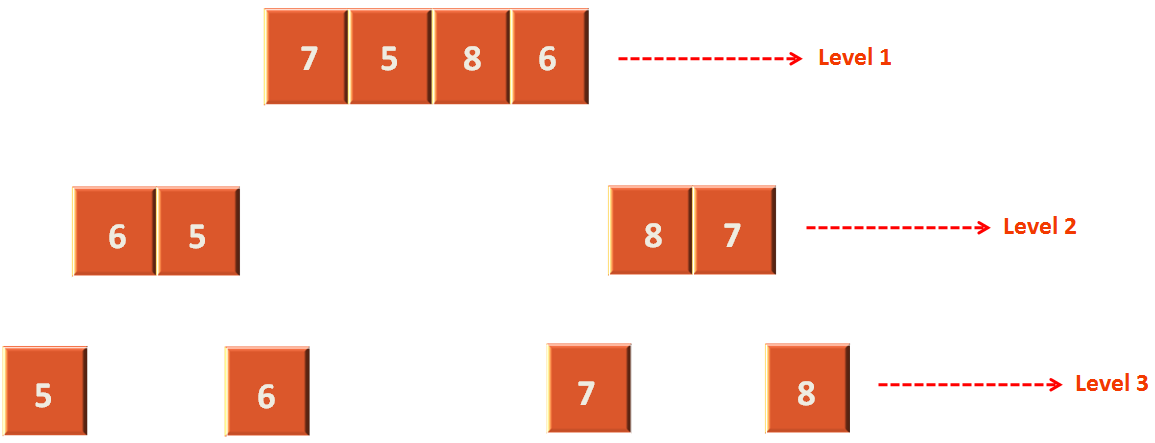
As as we have seen in the above case the array is divided exactly into two parts at all steps.
Thus, at each step the divide(...) method will take n times at each level. And how many levels are there. There are three levels or log n.
So, if we combine we get the,
Best case running time : O(n log n)
Now, lets say we are quite unlucky.
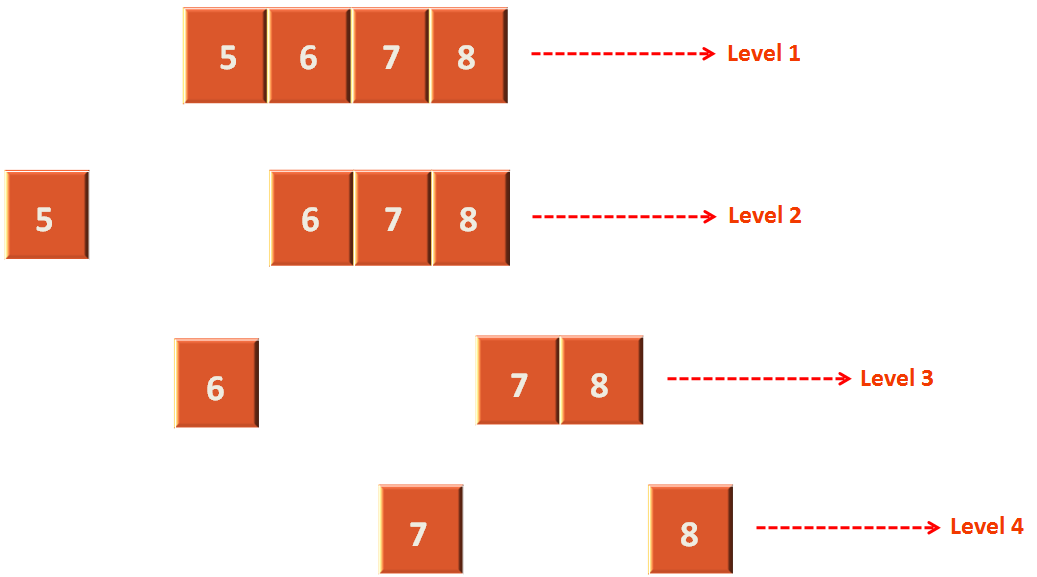
In the above array has 4 levels. In other words there are n levels. And also the divide(...) method is going to run n times at each level.
So, the
Worst case running time : O(n**2)
Average case running time : O(n log n)