

As we know, there is a three step process involved in Heap Sort:
We will be using arrays for implementing Heap and sort the values in descending order.
package main
import "fmt"
func heapify(arr []int, root int, length int) {
left := (2*root)+1
right := (2*root)+2
smallest := root
fmt.Println()
if (left < length && right <= length && arr[right] < arr[left]) {
smallest = right
} else if (left <= length) {
smallest = left
}
if (arr[root] > arr[smallest]) {
temp := arr[root]
arr[root] = arr[smallest]
arr[smallest] = temp
heapify(arr, smallest, length)
}
}
func buildHeap(arr []int) {
len := len(arr)-1
for parent := int((len-1)/ 2); parent >= 0; parent-- {
heapify(arr, parent, len)
}
}
func deleteMin(arr []int) {
len := len(arr)-1
// Extract elements one by one from Heap
for last := len; last > 0; last-- {
temp := arr[0]
arr[0] = arr[last]
arr[last] = temp
heapify(arr, 0, last-1);
}
}
func sort(arr []int) {
// Build heap (rearrange array)
buildHeap(arr)
deleteMin(arr)
}
func main() {
arr := []int{4,78,32,2,45,11}
fmt.Println("Array before Sorting")
for _, val := range arr {
fmt.Println(val)
}
sort(arr)
fmt.Println("Array after Sorting");
for _, val := range arr {
fmt.Println(val)
}
}
So, in the above code we have four methods:
The best thing about the methods are, they are quite self explanatory.
As we know, the process involved in HeapSort are :
And that's exactly what the above methods are doing.
The buildHeap(...) method is building the Heap. Also, buildHeap(...) method takes the help of Heapify(...) method to construct the Heap.
Then deleteMin(...) method comes into picture, which takes the minimum element from the root and places at the end of the array. Then uses Heapify(...) method to correct the Heap.
And, finally we have the sort(...) method, that clubs all the methods and gives us a sorted result.
Let us understand the entire flow :
Initially, we take the array,
arr := []int{4,78,32,2,45,11}And pass it to the sort(...) method,
sort(arr)
The sort(...) method is quite simple.
func sort(arr []int) {
// Build heap (rearrange array)
buildHeap(arr)
deleteMin(arr)
}It calls the buildHeap(...) method for building the array.
Then calls the deleteMin(...) method for deleting the minimum element from the the root and place it at the end of the array.
func buildHeap(arr []int) {
len := len(arr)-1
for parent := int((len-1)/ 2); parent >= 0; parent-- {
heapify(arr, parent, len)
}
}Let us understand the above method with the existing structure.
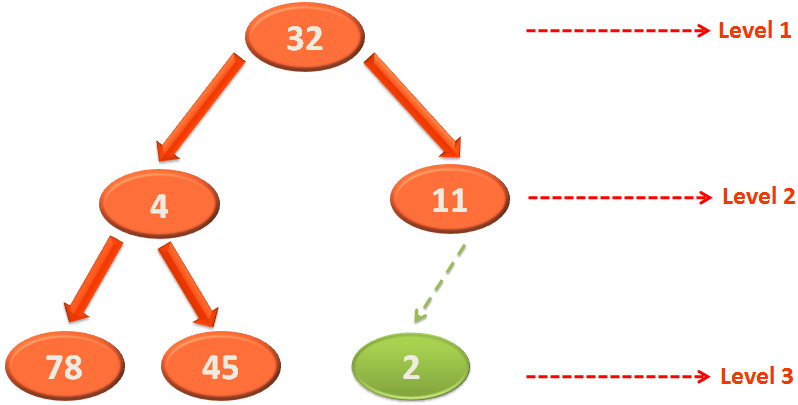
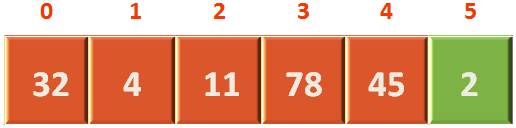
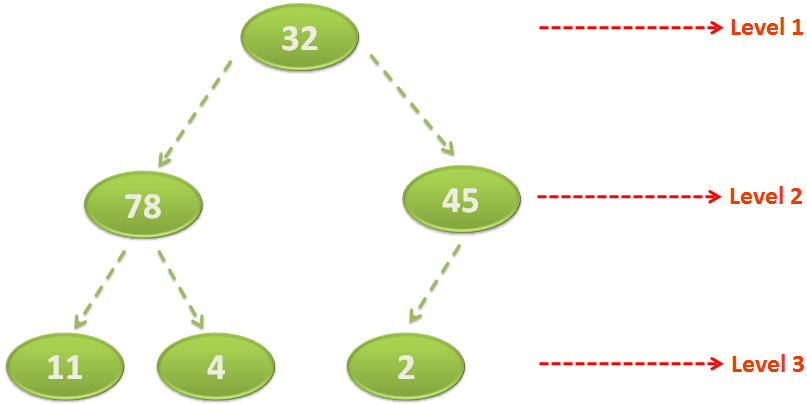
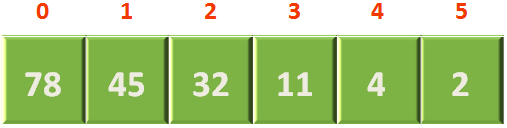
We have an array of 6 numbers,
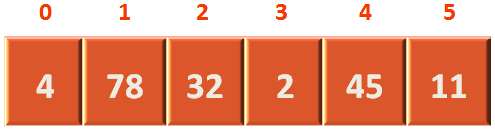
Let us form a logical binary tree with it,
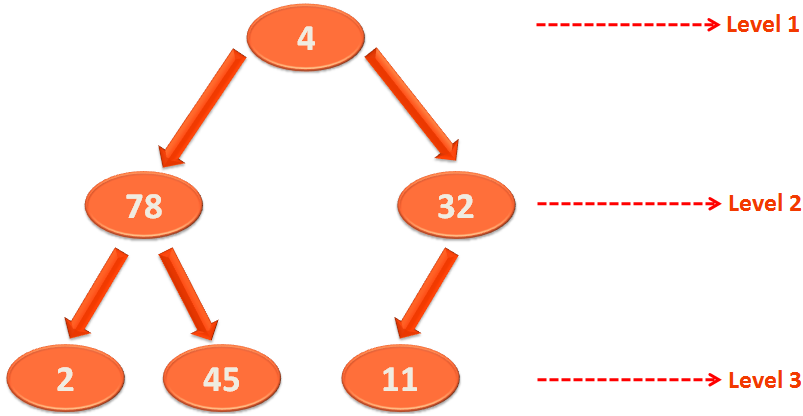
As we know, the elements in Level 3 satisfies the Heap property, as they don't have any child Nodes.
So, we need to target the Nodes of Level 2 and apply Heapify on them.
And that's exactly what we are doing,
for parent := int((len-1)/ 2); parent >= 0; parent-- {
heapify(arr, parent, len)
}We have taken the last element and calculated its parent.
i.e. The formula to calculate the parent is
parent = (element-1)/2
The position of last element is 5.
So,
parent := int((len-1)/ 2) parent = (5-1)/2 = 2
And the parent of arr[5] (i.e. 11) is arr[2] (i.e. 32).
So, the for loop becomes,
for parent = 2; parent >= 0; parent-- {
heapify(arr, parent, len)
}Now, is it clear ?
We are running the for loop, starting with the parents and applying Heapify on each of them.
Say for example, we will apply Heapify on 32 at first,
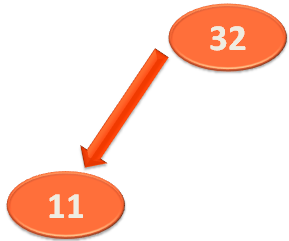
Then apply Heapify on,
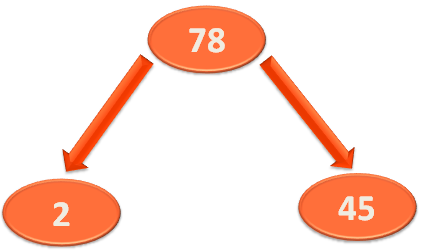
And loop goes on until it reaches the root.
func heapify(arr []int, root int, length int) {
left := (2*root)+1
right := (2*root)+2
smallest := root
fmt.Println()
if (left < length && right <= length && arr[right] < arr[left]) {
smallest = right
} else if (left <= length) {
smallest = left
}
if (arr[root] > arr[smallest]) {
temp := arr[root]
arr[root] = arr[smallest]
arr[smallest] = temp
heapify(arr, smallest, length)
}
}Let us take a small chunk of the Heap and understand the above Heapify code:
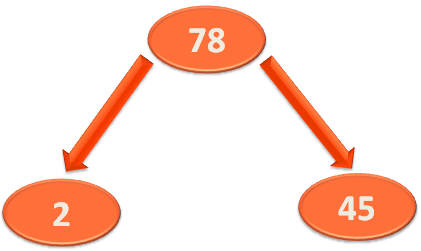
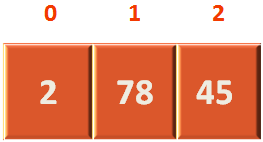
So, the array representation of the above Heap would be,
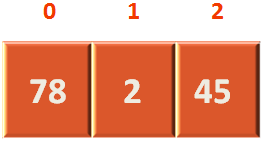
So the root variable would contain 0 and length variable would contain 2.
func heapify(arr []int, root int, length int)
Similarly, left variable would be 1.
left := (2*root)+1
As, left = (2*0)+1 = 1
And, right variable would be 2.
right := (2*root)+2
Next, we have initialised the smallest variable with the root variable(We will explain this soon).
smallest := root
The smallest variable denotes the position.
Now, let us revisit the logic of Heapify.
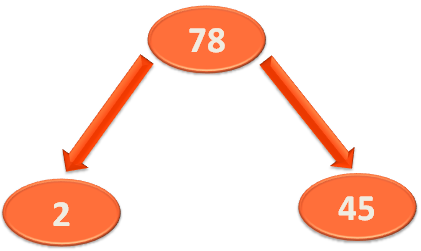
That's exactly we have done in the code.
if (left < length && right <= length && arr[right] < arr[left]) {
smallest = right
} else if (left <= length) {
smallest = left
}We are checking, if arr[right] is less than arr[left]. If so, we can consider right element is the smallest. And can initialise,
smallest = right
Else, we can suppose left element is the smallest element and can initialise,
smallest = left
To simplify,
arr[smallest] = 2 (Since, the left value is smaller than the right)
But what about the condition left < length && right <= length in the if statement and left <= length. Don't worry! We will explain it soon.
Now, since we have found out the smallest of left and right. According to the logic of Heapify,
And, so we have done,
if (arr[root] > arr[smallest]) {
temp := arr[root]
arr[root] = arr[smallest]
arr[smallest] = temp
heapify(arr, smallest, length)
}We have checked if the root element arr[root] (i.e. arr[0] or 78) is greater than arr[smallest] (i.e. arr[1] or 2).
If so, we swap it.
temp := arr[root] arr[root] = arr[smallest] arr[smallest] = temp
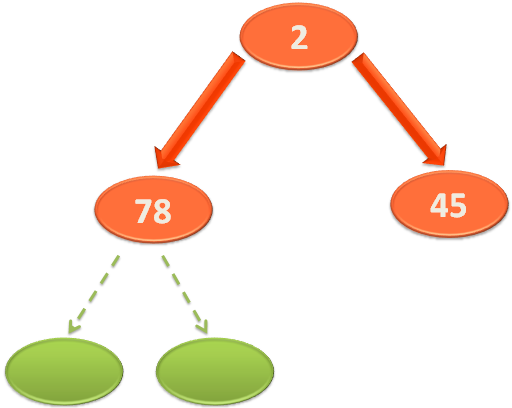
And the new Heap becomes.
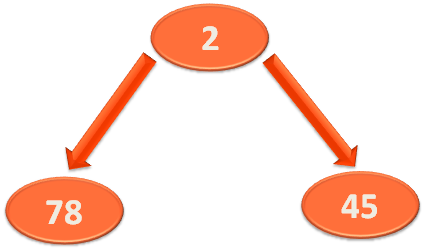
Then we make a recursive call to heapify(...) method, to check if there are any more children or not(In this case we have 3 elements but there can be more elements).
So, in the recursive call to heapify(...) method. We substitute the root variable with the smallest variable.
So, the heapify(...) method is called with the new set of values,
func heapify(arr []int, root int, length int)
Now, root = 1. (Because we have initialised smallest to root in the recursive call).i.e. root is pointing arr[1] where 78 lies.
But the strange thing is, left is referring to a location 3. That does not exist.
left := (2*root)+1 i.e. left = (2*1)+1 i.e. left = 3
At the same time right is referring to location 4. Which doesn't exist as well.
right := (2*root)+2 i.e. right = (2*1)+2 i.e. right = 4
Now, if we refer to arr[3] or arr[4], it will throw an ArrayIndexOutOfBounds exception.
And the below condition comes to rescue at this point.
if (left < length && right <= length && arr[right] < arr[left]) {
smallest = right
} else if (left <= length) {
smallest = left
}The condition left < length && right <= length checks, if the left and right element exists or not.
As in this case left and right element doesn't exist.
And the value of left is 3 and right is 4. But the value of length is 2.
So, the condition left < length && right <= length fails.
And it comes to the else statement,
else if (left <= length){
smallest = left
}Even this condition fails, as left is 3 and length is 2.
Now, the question would be, what would be the value of smallest?(As none of the if conditions met).
And, this is the time, the default initialisation of smallest variable comes into picture.
smallest := root
And the next if statement containing the recursive call to heapify(...) fails (Since, arr[root] is never greater than arr[root]. As root = smallest).
if (arr[root] > arr[smallest]) {
temp := arr[root]
arr[root] = arr[smallest]
arr[smallest] = temp
heapify(arr, smallest, length)
}And the method exits as the recursive call to heapify(...) fails.
So far we have dealt with the numbers 78, 2 and 45.
Let's take the bigger picture of the Binary Tree from the previous tutorial,
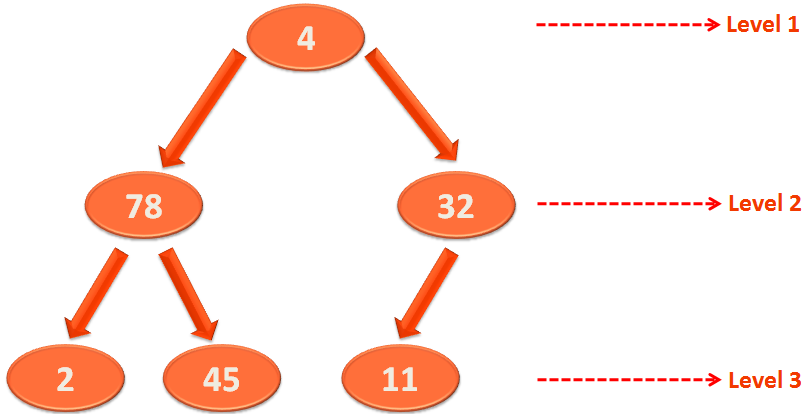
As we have seen, the buildHeap(...) method calls void heapify(int arr[],int root, int length) method.
Where the value of root variable is 2.
So, we will be applying Heapify on 32.
Just like the above explanation. We will compare left and right element.
if (left < length && right <= length && arr[right] < arr[left]) {
smallest = right
} else if (left <= length) {
smallest = left
}But the thing to be noted is, there is no right element.
And this is when the condition left <= length of else statement comes into picture.
Where smallestvariable is directly initialised with the left variable(Since, there is no right variable).
And the swapping happens and the heapify(...) method ends.
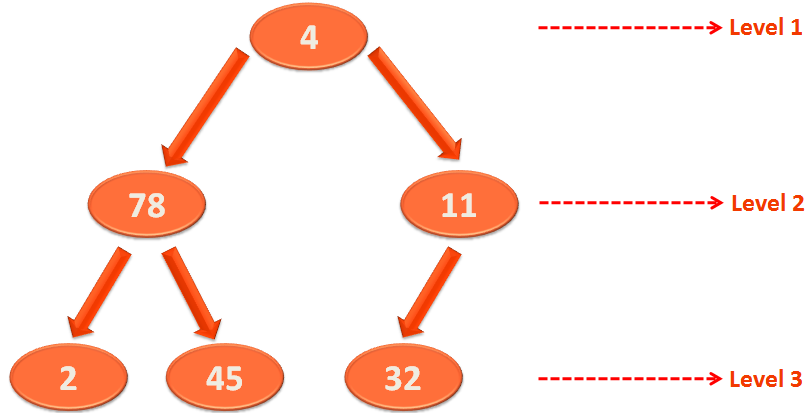
Again, control goes to buildHeap(...) method and heapify(...) is called again.
And 78 is dealt with.
Once again the swapping is done and control goes to buildHeap(...) method.
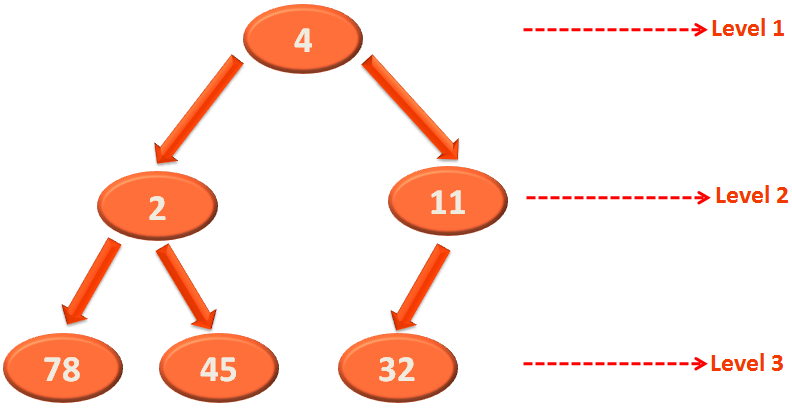
Now, the buildHeap(...) method calls heapify(...), dealing with the root element 4 finally.
As usual, we check if the left element i.e. 2 or the right element i.e. 11 is smaller and the swapping is done.
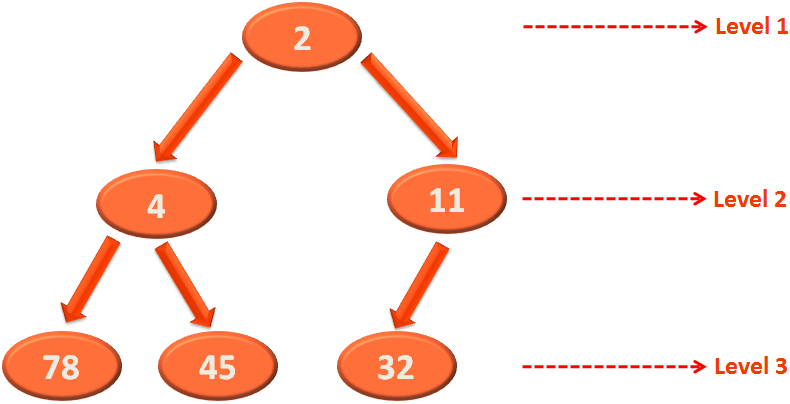
And the recursive call to heapify(...) is made making 4 the root element. And no change is made.
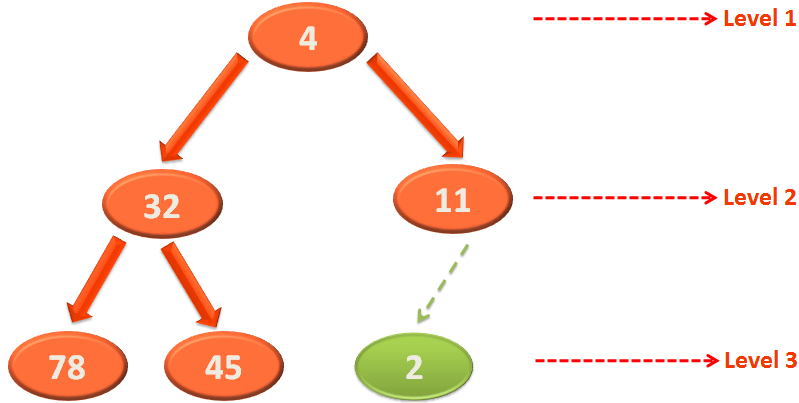
And finally, we get a Heap.
Now, comes the deleteMin(...) method for sorting.
func deleteMin(arr []int) {
len := len(arr)-1
// Extract elements one by one from Heap
for last := len; last > 0; last-- {
temp := arr[0]
arr[0] = arr[last]
arr[last] = temp
heapify(arr, 0, last-1)
}
}Let us take the above Heap,
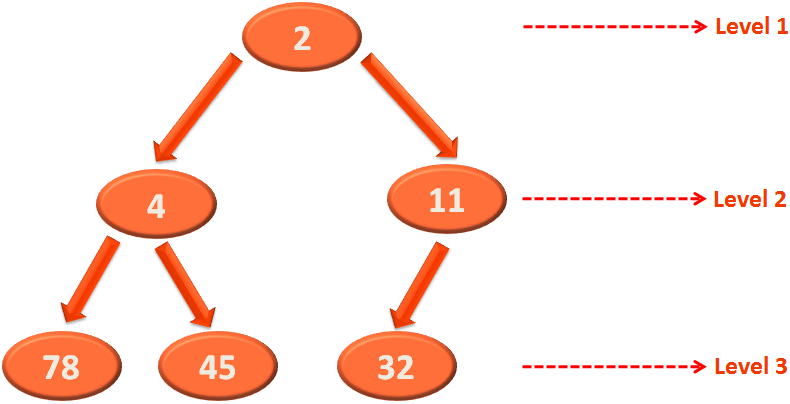
for last := len; last > 0; last--
temp := arr[0] arr[0] = arr[last] arr[last] = temp
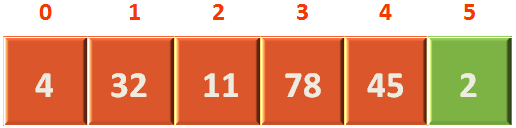
And, after completing the loop we get the final array in descending order.
There is a three step process involved in Heap Sort:
Now, if we analyse the running time.
Building a Heap can be done in O(n) time.
Removing the element takes O(log n) time.
Heapify takes O(log n) time.
Combining all the above running time, we get:
Total running time for Heap Sort : O(n log n)