

import sys
class Edge:
pass
global verticesKeyArray
def heapify(verticesArray, root, length):
left = (2*root)+1
right = (2*root)+2
smallest = root
if (left < length and right <= length and vertexVal[verticesArray[right]] < vertexVal[verticesArray[left]]):
smallest = right
elif (left <= length):
smallest = left
if (vertexVal.get(verticesArray[root]) > vertexVal.get(verticesArray[smallest])):
temp = verticesArray[root]
verticesArray[root] = verticesArray[smallest]
verticesArray[smallest] = temp
heapify(verticesArray, smallest, length)
def buildHeap():
global verticesKeyArray
verticesSet = vertexVal.keys()
# Now convert the above keys to an Array.
verticesArray = list(verticesSet)
for parent in range(int(((len(verticesArray)-1)-1)/ 2), -1, -1):
heapify(verticesArray, parent, len(verticesArray)-1)
verticesKeyArray = verticesArray.copy()
def updateHeap(vertex, length):
global verticesKeyArray
vertexVal[vertex] = length
verticesSet = vertexVal.keys()
# Now convert the above keys to an Array.
verticesArray = list(verticesSet)
for parent in range(int(((len(verticesArray)-1)-1)/ 2), -1, -1):
heapify(verticesArray, parent, len(verticesArray)-1)
verticesKeyArray = verticesArray.copy()
def containsVertex( vertex):
if vertex in vertexVal.keys():
return True
else:
return False
def delete_min():
global verticesKeyArray
temp = verticesKeyArray[0]
lengthArray = len(verticesKeyArray)-1
verticesKeyArray[0] = verticesKeyArray[lengthArray]
vertexVal.pop(temp)
verticesKeyArray = verticesKeyArray[:lengthArray]
if (lengthArray>0):
heapify(verticesKeyArray, 0, lengthArray-1)
return temp
def getWeight( vertex):
return vertexVal.get(vertex)
def empty():
global verticesKeyArray
if (len(verticesKeyArray) > 0):
return False
else:
return True
def primMST():
global vertexVal
vertexVal = {}
# Vertex to Edge Dictionary
vertexToEdge = {}
# Assign all the initial values as infinity for all the Vertices.
for v in vertices:
vertexVal[v] = sys.maxsize
# Call buildHeap() to create the MinHeap
buildHeap()
# Replace the value of start vertex to 0.
updateHeap("a",0)
# Continue until the Min-Heap is not empty.
while (empty() != True):
# Extract minimum value vertex from Map in Heap
currentVertex = delete_min()
# Need to get the edge for the vertex and add it to the Minimum Spanning Tree..
# Just note, the edge for the source vertex will not be added.
spanningTreeEdge = vertexToEdge.get(currentVertex)
if(spanningTreeEdge != None):
result.append(spanningTreeEdge)
# Get all the adjacent vertices and iterate through them.
for edge in getEdges(currentVertex):
adjacentVertex = edge.endVertex
# We check if adjacent vertex exist in 'Map in Heap' and length of the edge is with this vertex
# is greater than this edge length.
if(containsVertex(adjacentVertex) and getWeight(adjacentVertex) > edge.value):
# Replace the edge length with this edge weight.
updateHeap(adjacentVertex, edge.value)
vertexToEdge[adjacentVertex] = edge
def getEdges(vertex):
edgeList = []
i = vertices.index(vertex)
for iter in adjcList[i]:
edgeList.append(iter)
return edgeList
def constructAdjacencyList(vertex1, vertex2, edgeVal):
edge = Edge()
edge.startVertex = vertex1
edge.endVertex = vertex2
edge.value = edgeVal
adjcList.append([])
adjcList[vertices.index(vertex1)].append(edge)
def insertVertex(vertex):
vertices.append(vertex)
def printEdgeList():
for edge in result:
print("The Edge between", edge.startVertex ,"and", edge.endVertex, "is", edge.value)
adjcList = [[]]
vertices = []
vertexVal = {}
# Stores the Minimum spanning Tree
result = []
# Insert Vertices
insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")
# Create Adjacency List with Edges.
constructAdjacencyList("a", "b",1)
constructAdjacencyList("a", "c",5)
constructAdjacencyList("a", "d",4)
constructAdjacencyList("b", "a",1)
constructAdjacencyList("b" ,"e",8)
constructAdjacencyList("c", "a",5)
constructAdjacencyList("c", "d",12)
constructAdjacencyList("c", "e",9)
constructAdjacencyList("d", "a", 4)
constructAdjacencyList("d", "c", 12)
constructAdjacencyList("d", "e", 3)
constructAdjacencyList("e", "b", 8)
constructAdjacencyList("e", "c", 9)
constructAdjacencyList("e", "d", 3)
primMST()
printEdgeList()
Let us recapitulate the 3 step process for Prim's Algorithm :
Let us take the below graph, to understand the above code.
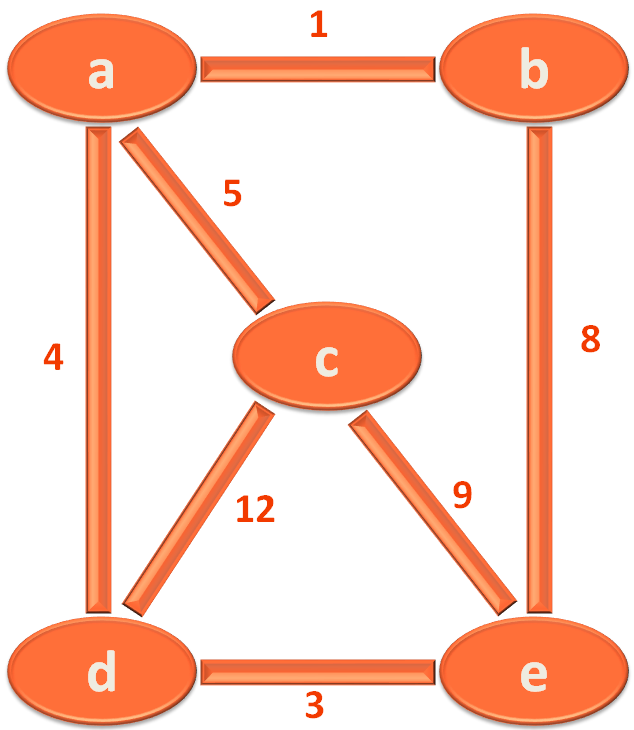
The first task is to construct the Graph. So, we need to store the Vertices first.
vertices = []
And also we know, we have to represent the edges as Adjacency List.
adjcList = [[]]
Eventually, in the main program. We have initialised the vertices,
# Insert Vertices
insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")And, created the Adjacency List with Edges.
# Create Adjacency List with Edges.
constructAdjacencyList("a", "b",1)
constructAdjacencyList("a", "c",5)
constructAdjacencyList("a", "d",4)
constructAdjacencyList("b", "a",1)
constructAdjacencyList("b" ,"e",8)
constructAdjacencyList("c", "a",5)
constructAdjacencyList("c", "d",12)
constructAdjacencyList("c", "e",9)
constructAdjacencyList("d", "a", 4)
constructAdjacencyList("d", "c", 12)
constructAdjacencyList("d", "e", 3)
constructAdjacencyList("e", "b", 8)
constructAdjacencyList("e", "c", 9)
constructAdjacencyList("e", "d", 3)Let us understand creation process of Adjacency List. If you already know it, you can skip.
Click Here - For the creation process of Adjacency List.
def constructAdjacencyList(vertex1, vertex2, edgeVal): edge = Edge() edge.startVertex = vertex1 edge.endVertex = vertex2 edge.value = edgeVal adjcList.append([]) adjcList[vertices.index(vertex1)].append(edge)
Let us take the example of the Edge (a,b) with length 1 and understand the above code.

constructAdjacencyList("a", "b", 1)Now, if we look at the method definition,
def constructAdjacencyList(vertex1, vertex2, edgeVal)
vertex1 is initialised with a.
vertex2 is initialised with b.
edgeVal is initialised with 1.
The next thing we do is, create an Edge object.
edge = Edge()
And initialise the Edge edge object with the start vertex, end vertex and the length of the Edge.
edge.startVertex = vertex1 edge.endVertex = vertex2 edge.value = edgeVal
And the Edge object looks somewhat like,

Now, since we have the Edge (a,b) initialised. The next task would be, to add this Edge to the AdjacencyList.
And as we have seen, there is a 2D LinkedList to store the Adjacency List.
adjcList = [[]]
Now, we will be creating the first row of LinkedList,
adjcList.append([])
And then we will try finding out, for which vertex we are going to insert the Edge.
adjcList[vertices.index(vertex1)].append(edge)
In simple words, vertices.index(vertex1) will tell us about the position of the start vertex.

In this case, the start vertex is a. And vertices.index(vertex1) will tell us about its position, i.e. 0.
So, if we substitute the line,
adjcList[vertices.index(vertex1)].append(edge)
With the value of vertices.index(vertex1),
adjcList[0].append(edge)
The edge would be added to the 0th location of the 2d LinkedList.
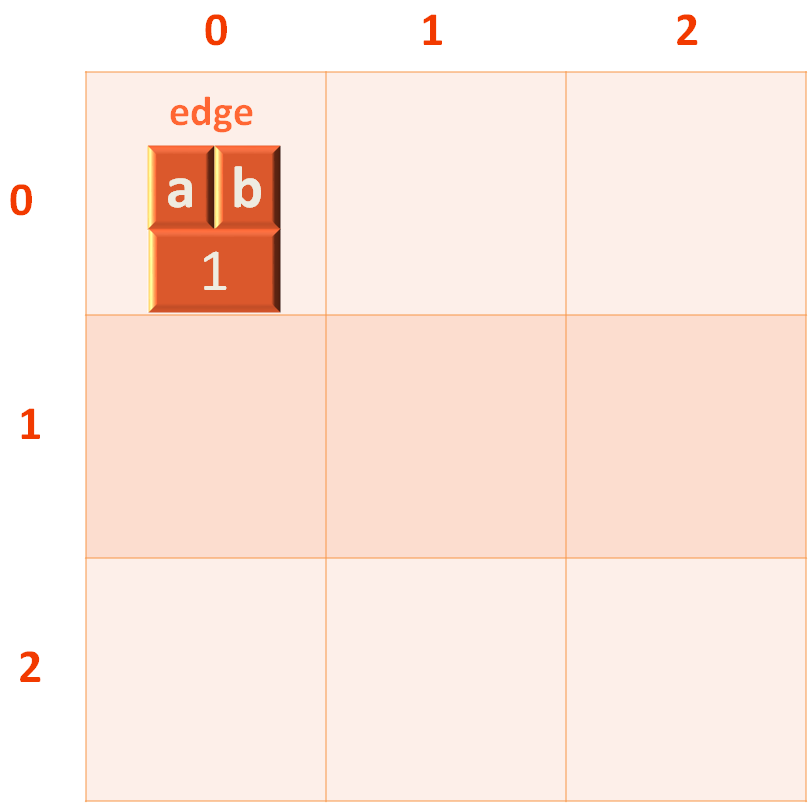
This is how a 2D LinkedList looks like. Just remember, the empty blocks are not yet created, but will be created eventually.
For now, only the first row is created with the first column where the edge

is inserted.
Next, when we try to insert the second adjacent edge of a i.e. a,c.
constructAdjacencyList("a", "c", 5)An edge object will be created
edge.startVertex = vertex1 edge.endVertex = vertex2 edge.value = edgeVal
And the Edge object looks somewhat like,

Once again the start vertex is a. And vertices.index(vertex1) will tell us about its position, i.e. 0.
So, if we substitute the line,
adjcList[vertices.index(vertex1)].append(edge)
With the value of vertices.index(vertex1),
adjcList[0].append(edge)
The edge would be added to the 1st row of the 2d LinkedList, just next to the first edge.
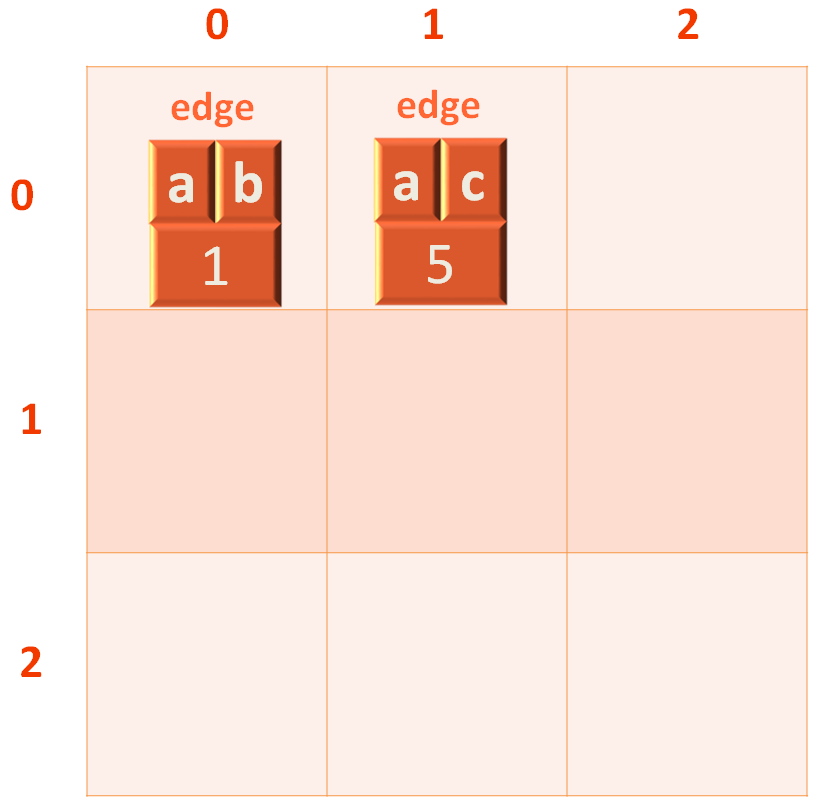
Similarly, we insert the third adjacent edge of a i.e. a,d.
constructAdjacencyList("a", "d", 4)An edge object will be created
edge.startVertex = vertex1 edge.endVertex = vertex2 edge.value = edgeVal
And the Edge object looks somewhat like,

Once again the start vertex is a. And vertices.index(vertex1) will tell us about its position, i.e. 0.
So, if we substitute the line,
adjcList[vertices.index(vertex1)].append(edge)
With the value of vertices.index(vertex1),
adjcList[0].append(edge)
The edge would be added to the 1st row of the 2d LinkedList, just next to the first edge.
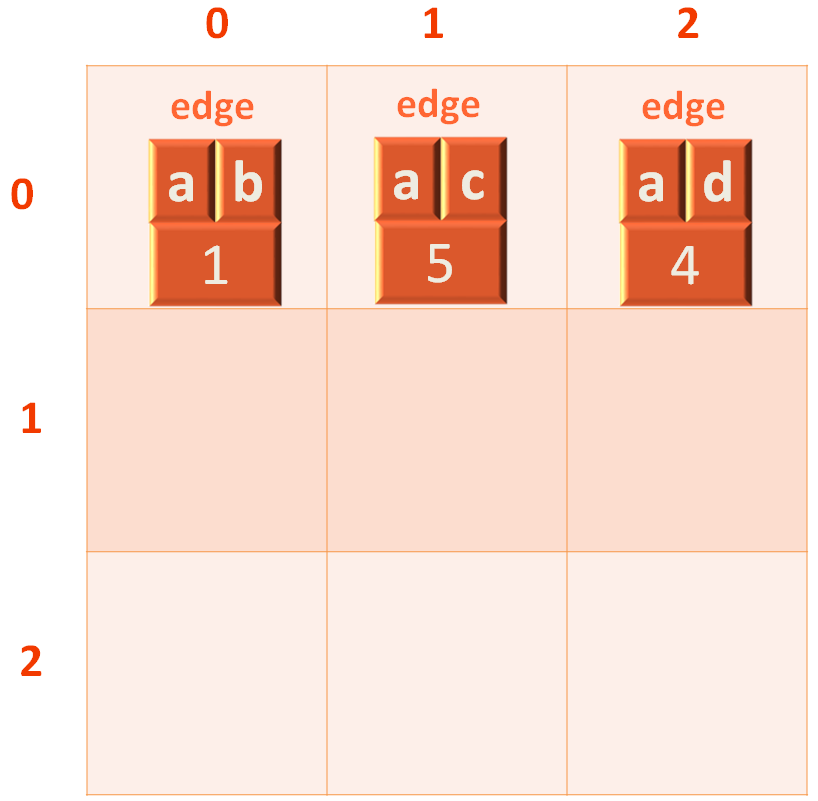
Similarly, we insert the adjacent edge of b i.e. b,a.
constructAdjacencyList("b", "a", 1);An edge object will be created
edge.startVertex = vertex1 edge.endVertex = vertex2 edge.value = edgeVal
And the Edge object looks somewhat like,

Now, the start vertex is b. And vertices.index(vertex1) will tell us about its position, i.e. 1.
So, if we substitute the line,
adjcList[vertices.index(vertex1)].append(edge)
With the value of vertices.index(vertex1),
adjcList[1].append(edge)
And this time, the edge would be added to the 2nd row of the 2d LinkedList.
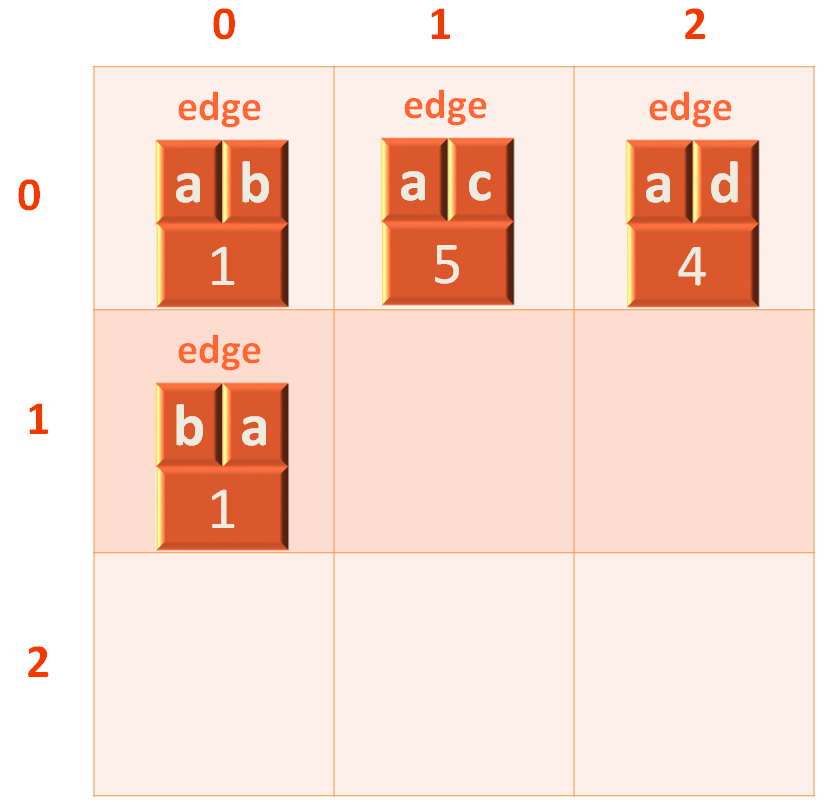
And eventually the AdjacencyList with Edges would be created with the 2D LinkedList.
Once we are done creating the AdjacencyList with Edges. The next task would be to call the actual method for Prim's Algorithm,
primMST()
Before we understand primMST() method in detail. Let us understand the Min-Heap Data Structure.
If you already know Min-Heap Data Structure, you can skip the below part.
Click Here - For Min-Heap Data Structure Recap.
There are four important method in the MinHeap class that are quite important.
They are :
Now, if we look at the primMST() method.
The Dictionary vertexVal is getting initialised here.
vertexVal = {}Where, vertexVal is a global variable.
global vertexVal
Next, we initialise the Dictionary with the vertices as key and assign the value as sys.maxsize. This sys.maxsize is so large that it could be compared with infinity.
# Assign all the initial values as infinity for all the Vertices. for v in vertices: vertexVal[v] = sys.maxsize

So, the Dictionary vertexVal is loaded with values.
Next, we call the build_heap() method to create the MinHeap, with the values of the Dictionary vertexVal.
buildHeap()
def buildHeap(): global verticesKeyArray verticesSet = vertexVal.keys() # Now convert the above keys to an Array. verticesArray = list(verticesSet) for parent in range(int(((len(verticesArray)-1)-1)/ 2), -1, -1): heapify(verticesArray, parent, len(verticesArray)-1) verticesKeyArray = verticesArray.copy()
Just remember, Dictionary is not a good Data Structure for Heap. Whereas array is an excellent Data Structure for Heap.
So, we take the keys from the Dictionary and create an Array out of it.
To do this, there is a two step process involved.
First, we extract the key from the Dictionary and put it into an dict_keys type variable.
verticesSet = vertexVal.keys()
Second, we create an Array/List and convert the Set to the Array/List.
verticesArray = list(verticesSet)
Then, we divide the Array into two parts and run a for loop. Then call the Heapify method.
for parent in range(int(((len(verticesArray)-1)-1)/ 2), -1, -1): heapify(verticesArray, parent, len(verticesArray)-1)
So, what does the heapify(..) method do?
Let us see.
def heapify(verticesArray, root, length): left = (2*root)+1 right = (2*root)+2 smallest = root if (left < length and right <= length and vertexVal[verticesArray[right]] < vertexVal[verticesArray[left]]): smallest = right elif (left <= length): smallest = left if (vertexVal.get(verticesArray[root]) > vertexVal.get(verticesArray[smallest])): temp = verticesArray[root] verticesArray[root] = verticesArray[smallest] verticesArray[smallest] = temp heapify(verticesArray, smallest, length)
Since, all the values of the Dictionary vertexVal are infinity now. So, it doesn't matter how the values will be inserted in the Min-Heap.

For the sake of understanding, let us understand the functionality of heapify(...) method.
So, we have passed the verticesArray, root element and the length of the Array to heapify(...) method.
Then, we have calculated the left, right and root element of the Heap.
left = (2*root)+1 right = (2*root)+2 smallest = root
Since, this is a Min-Heap. The smallest element would be at the root of the Heap.
So, we try initialising the smallest element with its right value.
And the below if condition checks, if the left and right element is less than the length of the Array.
if (left < length and right <= length and vertexVal[verticesArray[right]] < vertexVal[verticesArray[left]]): smallest = right elif (left <= length): smallest = left
And, if the element on the right side of the Dictionary vertexVal is less than the element on the right side.
vertexVal[verticesArray[right]] < vertexVal[verticesArray[left]]
Then element on the right side of the Dictionary is the smallest element.
smallest = right
And in the else part, we can assume that the element on the left side of the Dictionary has the smallest element.
smallest = left
Now, since we got the smallest element. We need to check if the actual root element is greater than the smallest element or not.
if (vertexVal.get(verticesArray[root]) > vertexVal.get(verticesArray[smallest])): temp = verticesArray[root] verticesArray[root] = verticesArray[smallest] verticesArray[smallest] = temp heapify(verticesArray, smallest, length)
And this is where, we swap the contents of the root element and the smallest element. Assuming the element in the root is greater than the smallest element.
Which shouldn't be. As the root element should always be the smallest element.
Then a recursive call is made to heapify(...) method.
heapify(verticesArray, smallest, length)
And the recursion continues until all the elements are arranged in MinHeap.
In the next line, we would update the value of source element a to 0.
# Replace the value of start vertex to 0.
updateHeap("a",0)Now, if we see the updateHeap(...) method,
def updateHeap(vertex, length): global verticesKeyArray vertexVal[vertex] = length verticesSet = vertexVal.keys() # Now convert the above keys to an Array. verticesArray = list(verticesSet) for parent in range(int(((len(verticesArray)-1)-1)/ 2), -1, -1): heapify(verticesArray, parent, len(verticesArray)-1) verticesKeyArray = verticesArray.copy()
The first thing we do is, replace the value in the Dictionary vertexVal.
vertexVal[vertex] = length
Then we follow the same process we followed above. i.e. Extract the keys from the Dictionary. And convert into an Array.
verticesSet = vertexVal.keys() # Now convert the above keys to an Array. verticesArray = list(verticesSet)
Then we call the heapify(...) method. Because we have updated a new value and in that case the Heap has to be rearranged to form a Min-Heap.
Now, that we have understood Min-Heap. Let us understand the details about the actual method that calculates the Minimum Spanning Tree using Prim's Algorithm.
def primMST():
global vertexVal
vertexVal = {}
# Vertex to Edge Dictionary
vertexToEdge = {}
# Assign all the initial values as infinity for all the Vertices.
for v in vertices:
vertexVal[v] = sys.maxsize
# Call buildHeap() to create the MinHeap
buildHeap()
# Replace the value of start vertex to 0.
updateHeap("a",0)
# Continue until the Min-Heap is not empty.
while (empty() != True):
# Extract minimum value vertex from Map in Heap
currentVertex = delete_min()
# Need to get the edge for the vertex and add it to the Minimum Spanning Tree..
# Just note, the edge for the source vertex will not be added.
spanningTreeEdge = vertexToEdge.get(currentVertex)
if(spanningTreeEdge != None):
result.append(spanningTreeEdge)
# Get all the adjacent vertices and iterate through them.
for edge in getEdges(currentVertex):
adjacentVertex = edge.endVertex
# We check if adjacent vertex exist in 'Map in Heap' and length of the edge is with this vertex
# is greater than this edge length.
if(containsVertex(adjacentVertex) and getWeight(adjacentVertex) > edge.value):
# Replace the edge length with this edge weight.
updateHeap(adjacentVertex, edge.value)
vertexToEdge[adjacentVertex] = edgeThree things to remember :
Now, let us look at the steps involved :
vertexVal = {}vertexToEdge = {}for v in vertices: vertexVal[v] = sys.maxsize

buildHeap()
updateHeap("a",0)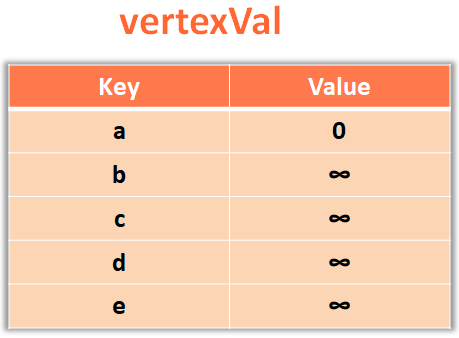
while (empty() != True): # Extract minimum value vertex from Map in Heap currentVertex = delete_min() # Need to get the edge for the vertex and add it to the Minimum Spanning Tree.. # Just note, the edge for the source vertex will not be added. spanningTreeEdge = vertexToEdge.get(currentVertex) if(spanningTreeEdge != None): result.append(spanningTreeEdge) # Get all the adjacent vertices and iterate through them. for edge in getEdges(currentVertex): adjacentVertex = edge.endVertex # We check if adjacent vertex exist in 'Map in Heap' and length of the edge is with this vertex # is greater than this edge length. if(containsVertex(adjacentVertex) and getWeight(adjacentVertex) > edge.value): # Replace the edge length with this edge weight. updateHeap(adjacentVertex, edge.value) vertexToEdge[adjacentVertex] = edge
currentVertex = delete_min()

spanningTreeEdge = vertexToEdge.get(currentVertex) if(spanningTreeEdge != None): result.append(spanningTreeEdge)
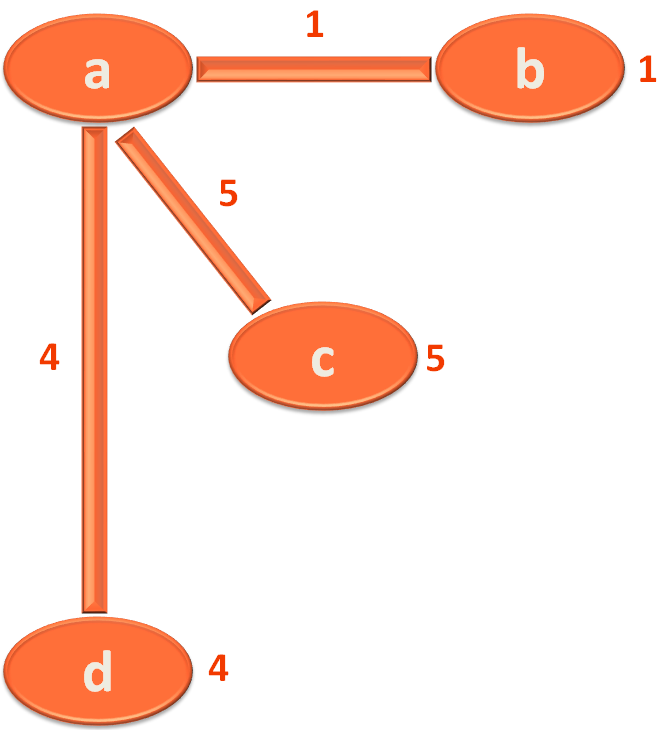
for edge in getEdges(currentVertex):
adjacentVertex = edge.endVertex
# We check if adjacent vertex exist in Map in Heap and length of the edge is with this vertex
# is greater than this edge length.
if(containsVertex(adjacentVertex) and getWeight(adjacentVertex) > edge.value):
# Replace the edge length with this edge weight.
updateHeap(adjacentVertex, edge.value)
vertexToEdge[adjacentVertex] = edge
adjacentVertex = edge.endVertex

if(containsVertex(adjacentVertex) and getWeight(adjacentVertex) > edge.value): # Replace the edge length with this edge weight. updateHeap(adjacentVertex, edge.value) vertexToEdge[adjacentVertex] = edge
updateHeap(adjacentVertex, edge.value)
vertexToEdge[adjacentVertex] = edge
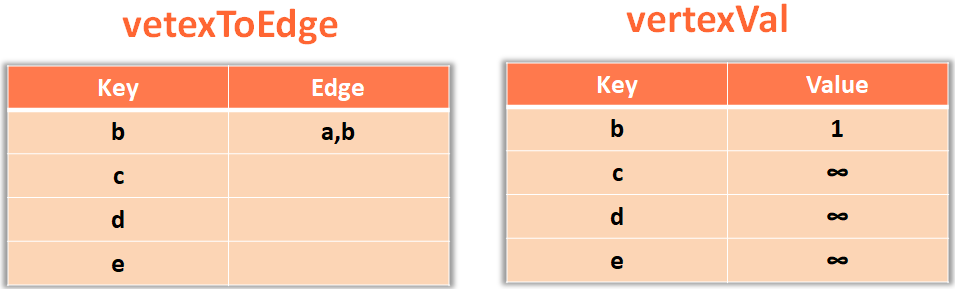
The similar process gets repeated and we get the Minimum Spanning Tree using Prim's Algorithm.
The time complexity of Prim's Algorithm for Minimum Spanning Tree is : O(E logV)
Where E is the Edge
And V is the Vertex
The time complexity O(E logV) is only when we will be using the above combination of MIn-Heap and Adjacency List.