RUBY - BELLMAN FORD'S ALGORITHM - CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

class Edge
	attr_accessor :startVertex, :endVertex, :value
end

def insertVertex(vertex)
	$vertices.push(vertex)
end	

def insertEdge(vertex1, vertex2, edgeVal)
	edge = Edge.new()
	edge.startVertex = vertex1
	edge.endVertex = vertex2
	edge.value = edgeVal

	$edgeList.push(edge)
end	

def getShortestPath(sourceVertex)
	$vertexDistance = {}
	$vertexParent = {}

	#Set the initial distance of every vertex to infinity
	for vertex in $vertices
		$vertexDistance[vertex] = (2**(0.size * 8 -2) -1)
		$vertexParent[vertex] = nil
	end	

	#Initialise the distance of source vertex to be 0
	$vertexDistance[sourceVertex] = 0

	verLen = $vertices.length

	for i in 0..verLen - 2
		for edge in $edgeList
			u = edge.startVertex
			v = edge.endVertex
                
            #relax the edge
			if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
				$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
				$vertexParent[v] = u
			end
		end
	end			


    #Relax all the edges again. If we are still getting a lesser distance then 
    #there is negative weight cycle in the graph. 
	for edge in $edgeList
		u = edge.startVertex
		v = edge.endVertex
		if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
			print("The Graph contains negative weight cycle \n")
			return
		end
	end
end			

def printShortestPath()
	for x in $vertexDistance.keys
		print("The shortest distance between a and ",x," is ",$vertexDistance[x],"\n")
	end
end		


$vertexDistance
$vertexParent
$vertices = []
$edgeList = []

# Adding $vertices one by one

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")
        
#Adding edges with values.

insertEdge("a", "b", 18)
insertEdge("a", "c", 2)
insertEdge("a", "d", 4)

insertEdge("c", "e", 1)

insertEdge("e", "b", 5)

insertEdge("d", "c", 12)
insertEdge("d", "e", 3)

getShortestPath("a")

printShortestPath()

Output :

The shortest distance between a and a is 0
The shortest distance between a and b is 8
The shortest distance between a and c is 2
The shortest distance between a and d is 4
The shortest distance between a and e is 3

Code explanation for Bellman Ford's Algorithm - Single Source Sortest path

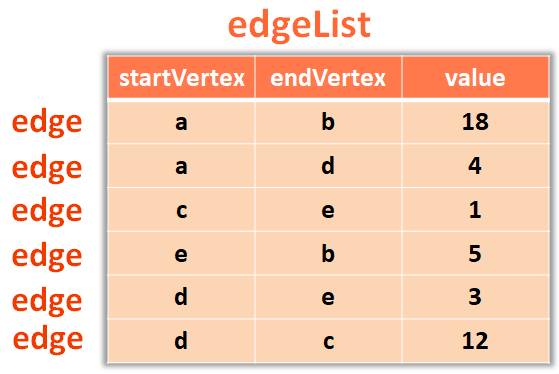
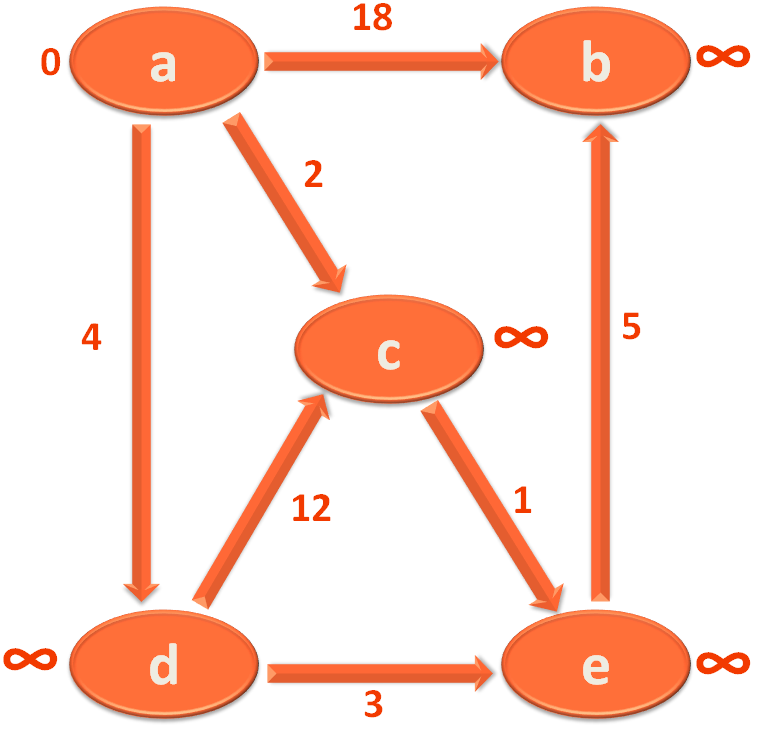
For explanation purpose we will be taking the below Graph :

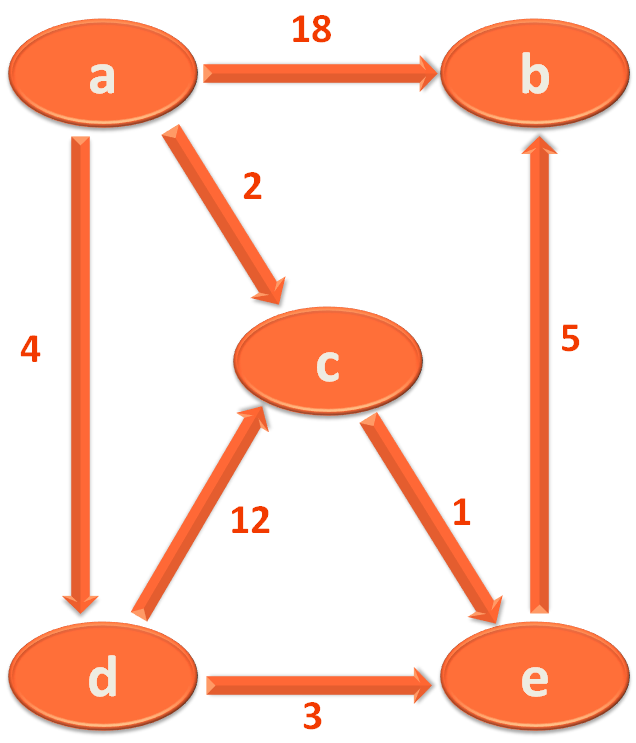
So, the first thing we will do is construct create a List,

$vertices = []

And store all the Vertices there,

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")

The next thing we would do is, list out all the Edges.

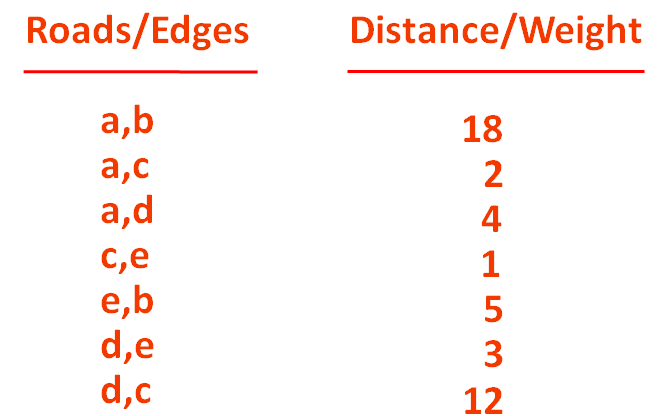
So, we would create a List,

$edgeList = []

And store all the Edges in the edgeList,

insertEdge("a", "b", 18)
insertEdge("a", "c", 2)
insertEdge("a", "d", 4)

insertEdge("c", "e", 1)

insertEdge("e", "b", 5)

insertEdge("d", "c", 12)
insertEdge("d", "e", 3)

And we have the method insertEdge(...) that initialises the Edges,

def insertEdge(vertex1, vertex2, edgeVal)
	edge = Edge.new()
	edge.startVertex = vertex1
	edge.endVertex = vertex2
	edge.value = edgeVal

	$edgeList.push(edge)
end

The insertEdge(...) method is quite simple to understand. We already have the Edge class :

class Edge
	attr_accessor :startVertex, :endVertex, :value
end

We have created an Edge object,

edge = Edge.new()

And initialised the values,

edge.startVertex = vertex1
edge.endVertex = vertex2
edge.value = edgeVal

Finally, added the edge object to the List edgeList.

edgeList.push(edge)

And one by one, we add all the edges to the List edgeList. And, finally the List edgeList has all the Edges in it.

Now, since we have all the edges in the List edgeList. It is time for us to call the method getShortestPath(...) by passing the start vertex a to it.

getShortestPath("a")

Explanation of def getShortestPath(sourceVertex) method :

def getShortestPath(sourceVertex)
	$vertexDistance = {}
	$vertexParent = {}

	#Set the initial distance of every vertex to infinity
	for vertex in $vertices
		$vertexDistance[vertex] = (2**(0.size * 8 -2) -1)
		$vertexParent[vertex] = nil
	end

	#Initialise the distance of source vertex to be 0
	$vertexDistance[sourceVertex] = 0

	verLen = $vertices.length

	for i in 0..verLen - 2
		for edge in $edgeList
			u = edge.startVertex
			v = edge.endVertex

			#relax the edge
			if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
				$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
				$vertexParent[v] = u
			end
		end
	end

	#Relax all the edges again. If we are still getting a lesser distance then
	#there is negative weight cycle in the graph.
	for edge in $edgeList
		u = edge.startVertex
		v = edge.endVertex
		if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
			print("The Graph contains negative weight cycle \n")
			return
		end
	end
end

So, what we have done is, created two Maps.

The first Map vertexDistance stores vertex as key and the value as the one we were marking each vertex with.

$vertexDistance = {}

In simple words,

If we take the example of the Edge a,b with value 18.

The Vertex a is marked with 0 and Vertex b is marked with 18.

So, the Map vertexDistance stores Vertex a as key and 0 as value.

Similarly, the Map vertexDistance stores Vertex b as key and 18 as value.

Quite clear!

Now, let us see the second Map,

$vertexParent = {}

The second Map vertexParent stores vertex as key and the value as its immediate source vertex.

If we take the same example of the Edge a,b with value 18.

So, the Map vertexParent stores Vertex b as key and vertex a as value.

Similarly, if we take the example of the Edge d,e with length 3.

Then the Map vertexParent stores Vertex e as key and vertex d as value.

Fair enough !

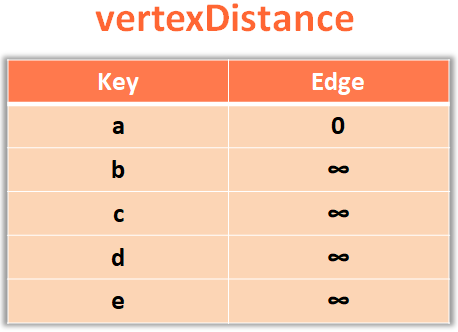
So, the next thing we will do is, mark all the Vertices with ∞ except the starting vertex a, which should be marked with 0.

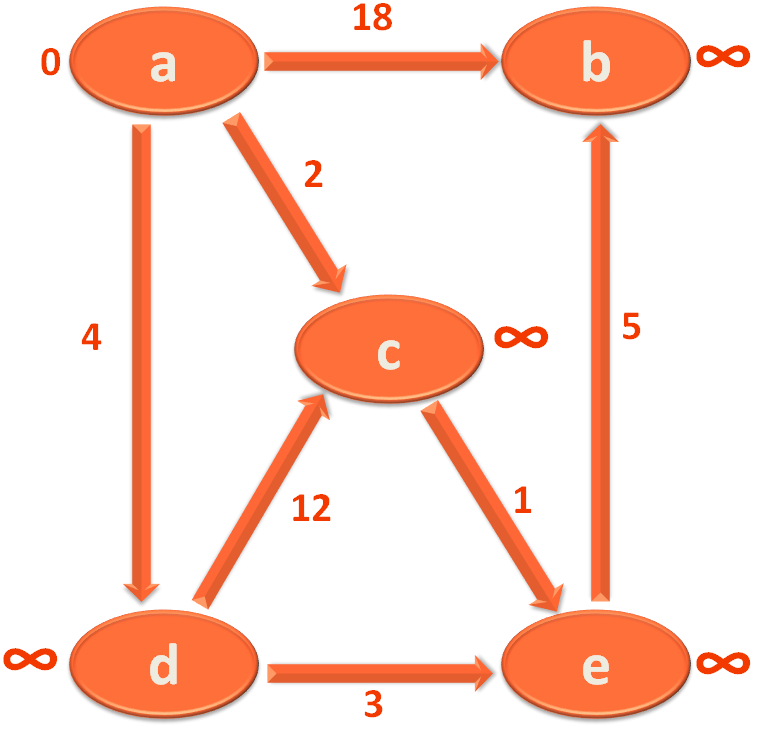
And to do this we will take all the Vertices one by one and put in the Map vertexDistance and initialise the value of each Vertex to ∞ or sys.maxsize.

And at the same time, take the vertices and put in the Map vertexParent and initialise the value of each Vertex to nil.

#Set the initial distance of every vertex to infinity
for vertex in $vertices
	$vertexDistance[vertex] = (2**(0.size * 8 -2) -1)
	$vertexParent[vertex] = nil
end
#Initialise the distance of source vertex to be 0
$vertexDistance[sourceVertex] = 0

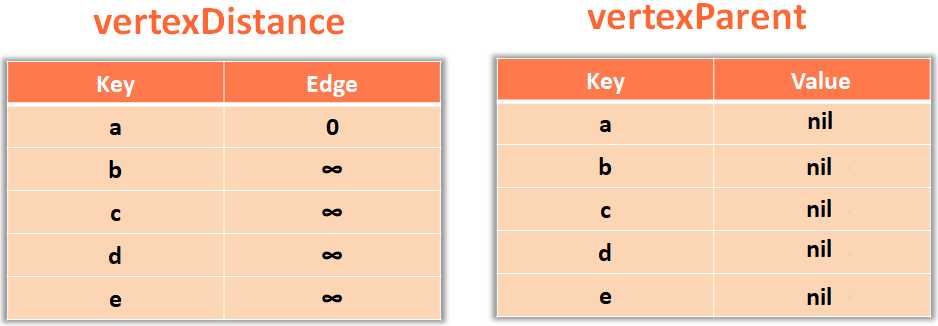
Then comes the for loop where in each iteration the marking and relaxing process takes place. And we iterate it verLen-2 times. Where verLen is the number of Vertices.

verLen = $vertices.length

for i in 0..verLen-2
	for edge in $edgeList
		u = edge.startVertex
		v = edge.endVertex

		#relax the edge
		if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
			$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
			$vertexParent[v] = u
		end
	end
end

The above for loop is quite simple.

As said we iterate the for loop verLen-2 times.

for i in 0..verLen-2

There is a nested for loop inside it. Which collects all the edges from the List edgeList,

And iterates through all the edges from the List edgeList, one by one.

	for edge in $edgeList
		u = edge.startVertex
		v = edge.endVertex

		#relax the edge
		if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
			$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
			$vertexParent[v] = u
		end
	end

So, in the above nested for loop, it takes the the first edge,

And the startVertex i.e. a is put in a String u,

u = edge.startVertex

and the endVertex i.e. b is put in a String v.

v = edge.endVertex

So, u would contain vertex a and v would contain the vertex b.

Next, we come across the line that has the if statement. Where the actual relaxation process takes place.

#relax the edge
if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
	$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
	$vertexParent[v] = u
end

So, if we have a closer look at the if statement,

if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))

The if statement has,

vertexDistance.fetch(u)

edge.value

vertexDistance.fetch(v)

The vertexDistance is a Hash that has the Key as Vertex name and value as the value marked with the current vertex.

Currently all the vertices are marked with ∞. Except the starting vertex a which is marked with 0.

Now, let us relook the condition inside if statement.

if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))

The variable u has the value a inside it.

So, vertexDistance.fetch(u) gives us 0(As the value associated with the key a is 0 in vertexDistance Hash).

Similarly, vertexDistance.fetch(v) gives us ∞(As the value associated with the key b is ∞ in vertexDistance Hash).

And edge.value gives us 18 (Because the current edge we are dealing with is a,b with value 18).

Now, if we see the add operation,

vertexDistance.fetch(u) + edge.value

It would be 0 + 18, i.e. 18

and check if the added value 18 is less than vertexDistance.get(v) (i.e. ∞).

if (vertexDistance.fetch(u) + edge.value < vertexDistance.fetch(v))

And obviously, 18 is less than ∞.

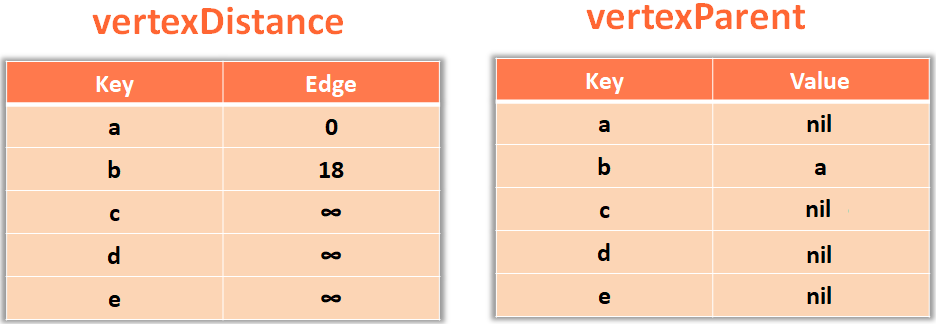
So, we get into the if block and relax/replace the new added value vertexDistance.fetch(u) + edge.value i.e. 18 to the value of vertex b

vertexDistance[v] = vertexDistance.fetch(u) + edge.value

At the same time change the parent of b to a in vertexParent.

Note : In the Map 'vertexDistance', we are storing the vertex and its marked distance (i.e. Vertex 'b' and 18). And to track the immediate parent of vertex 'b' we are using the Map 'vertexParent'. Where we are storing the immediate parent of 'b' in parallel.

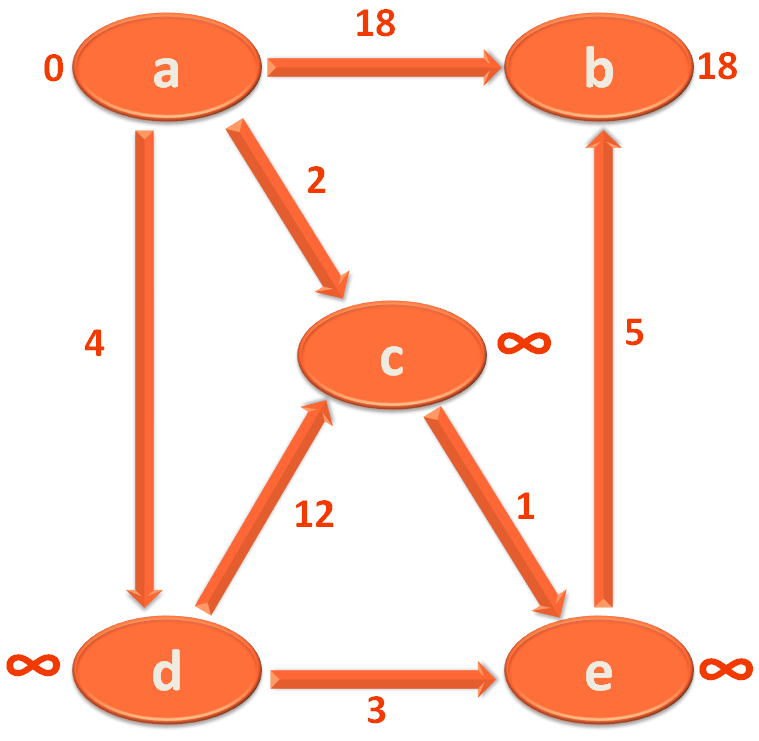
Same way we have to take the next edge and continue with the for loop.

for edge in $edgeList
	u = edge.startVertex
	v = edge.endVertex

	#relax the edge
	if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
		$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value
		$vertexParent[v] = u
	end
end

So, the next edge in the List edgeList is,

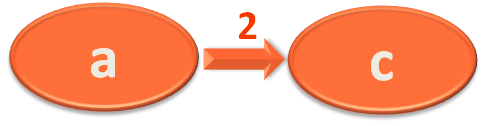
Similarly we take the startVertex and endVertex of edge object in u and v.

So, right now u has a and v has c.

Next, we add the current value of vertex a in vertexDistance (i.e. 0) and the current value of the edge (i.e. 2)

$vertexDistance.fetch(u) + edge.value

and check if the added value(i.e. 2) is less than the value of vertex d in vertexDistance (i.e. ∞).

if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))

And obviously, 2 is less than ∞.

So, we get into the if block and relax/replace the new added value vertexDistance.get(u) + edge.value i.e. 2 to the value of vertex c

$vertexDistance[v] = $vertexDistance.fetch(u) + edge.value

At the same time change the parent of c to a in vertexParent.

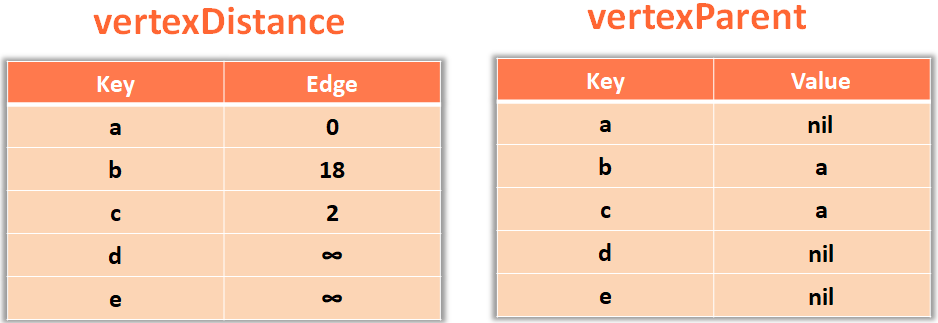
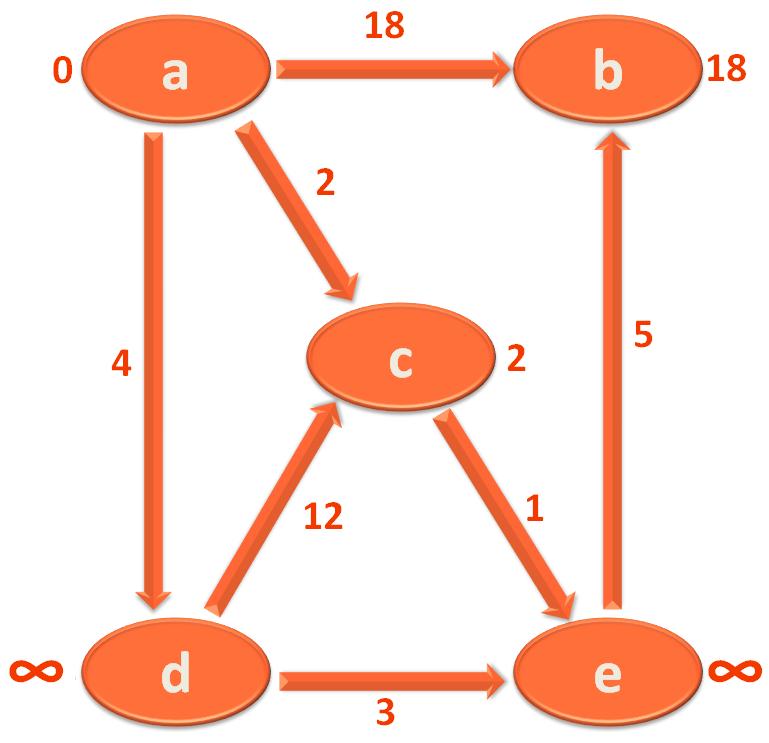
And if we continue the same process, we get the Stortest Path from source vertex a to all the other Vertices.

Well ! We are not done yet.

What if there is a negative weight cycle ?

And we have the code to deal with negative weight cycle.

#Relax all the edges again. If we are still getting a lesser distance then
#there is negative weight cycle in the graph.
for edge in $edgeList
	u = edge.startVertex
	v = edge.endVertex
	if ($vertexDistance.fetch(u) + edge.value < $vertexDistance.fetch(v))
		print("The Graph contains negative weight cycle \n")
		return
	end
end

The above code is quite simple to understand.

We usually continue iterating (V-1) times. Where V is the number of vertices. In this case we iterate V times. And if the weight reduces then there is a negative weight cycle.

Running time of Bellman Ford Algorithm

Since we are running a nested for loop.

So, the running time is : O(VE)

Where V is the number of Vertices

And E is the number of Edges.

❮❮ PREV