

#include <iostream>
using namespace std;
class Sort {
public:
void selectionSort(int arr[], int size) {
int currentMaximum;
int temp;
for (int i=0; i < size; i++) {
currentMaximum = 0;
// Considering the first element to be the maximum element of the unsorted array.
// And, (size-i) is to ignore the comparisons that is already done.
for(int j = 1; j < size-i; j++) {
if (arr[j] > arr[currentMaximum]) {
currentMaximum = j;
}
}
// Swap the Current Maximum element with the last element.
temp = arr[size-i-1];
arr[size-i-1] = arr[currentMaximum];
arr[currentMaximum] = temp;
}
}
};
int main() {
int arr[] = {7, 4, 8, 1, 6};
int size = sizeof(arr) / sizeof(arr[0]);
Sort sort;
sort.selectionSort(arr, size);
for(int i=0; i < size; i++) {
cout << arr[i] << ", ";
}
}
In the main() method, we have the array,
int arr[] = {5, 3, 6, 2, 1, 4};Then, we have calculated the size of the array,
int size = sizeof(arr) / sizeof(arr[0]);
Then we have passed the array and the size of the array to the bubbleSort(..) method,
Also note that,
int currentMaximum;
currentMaximum is going to hold the position of the Current Maximum value. I will clear it below.
Now, let us corelate this code with the explanation of Selection Sort.
Let us take the same values defined above.

And take the chunk of code and explain it.
for (int i=0; i < size; i++) {
currentMaximum = 0;
// Considering the first element to be the maximum element of the unsorted array.
// And, (size-i) is to ignore the comparisons that is already done.
for(int j = 1; j < size-i; j++) {
if (arr[j] > arr[currentMaximum]) {
currentMaximum = j;
}
}
// Swap the Current Maximum element with the last element.
temp = arr[size-i-1];
arr[size-i-1] = arr[currentMaximum];
arr[currentMaximum] = temp;
}So, the outer loop, i.e.
for (int i=0; i < size; i++)
Determines the Passes. If you see the above explanation you can find the first pass,
In the next step we have initialized the currentMaximum to 0.
currentMaximum = 0;
Because no matter what we have to initialize the currentMaximum to 0 at the end of every pass.
Then comes the the inner loop, i.e.
for(int j = 1; j < size-i; j++)
Which determines the iterations.
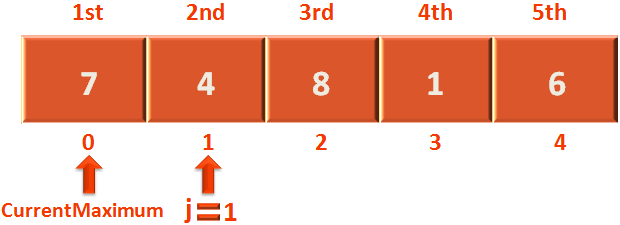
Next, comes the comparison part where we compare 2nd element with the currentMaximum. Now, since currentMaximum is at the 0th position of the Array. We compare if 4 is greater than 7 or not.
if (arr[j] > arr[currentMaximum]) {
currentMaximum = j;
}Let, us also look at the 2nd iteration.
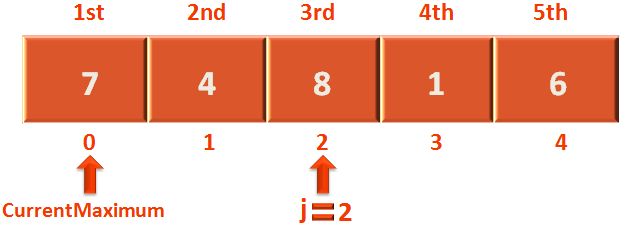
In the above diagram we can see that j is 2. And if we refer to the code,
if (arr[j] > arr[currentMaximum]) {
currentMaximum = j;
}a[j] is 8 and arr[currentMaximum] is 7. And 8 is greater than 7. So, we initialize currentMaximum with 2.
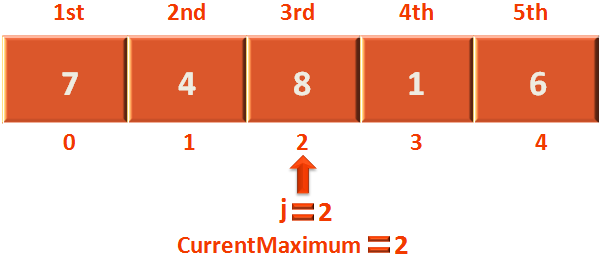
And in the next iteration j is increased by 1 and refers to the 3 in array,
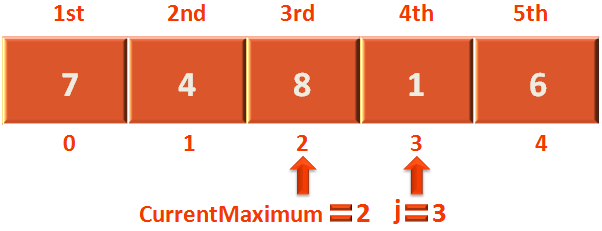
In the next iteration j is increased by 1. And when we reach at the end of the pass(i.e. When j becomes 4),
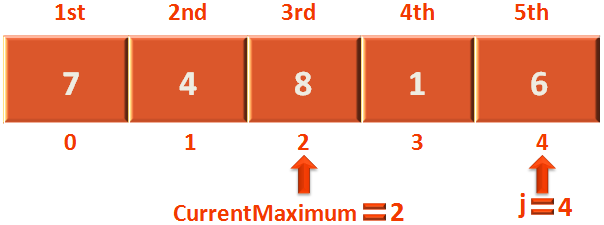
We swap the currentMaximum with the last element.
temp = arr[size-i-1]; // (size-i-1) is (5-0-1) i.e. 4 arr[size-i-1] = arr[currentMaximum]; // currentMaximum is 2 arr[currentMaximum] = temp;
So, as mentioned we swap arr[size-i-1] 1.e. arr[2] with arr[currentMaximum] i.e. arr[4]
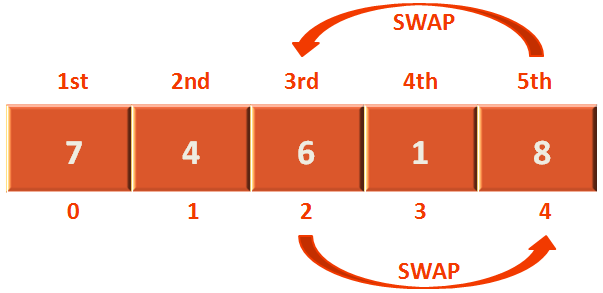
And continue in the same pattern.
If we consider the Selection Sort Algorithm, there are two loops. Firstly, there is the for loop. And inside the for loop there is also a for loop.
The for loop executes n times(Assuming the array contains n elements).
Now, for each iteration of for loop, the nested for loop also executes approximately n times.
Which means for 1st iteration of for loop,
the nested for loop also runs n time.Similarly, for 2nd iteration of for loop,
inner for loop runs (n-1) times.Similarly, for nth iteration of for loop,
inner for loop runs 1 time.So, the running time is close to n*n or n^2.
So, in worst case the running time is O(n^2).