BELLMAN FORD's ALGORITHM - CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

import java.util.*;

class Edge {

    String startVertex;
    String endVertex;

    int value;
}

public class BellmanFordSSSP {

    LinkedList<String> vertices;
    LinkedList<Edge> edgeList;

    Map<String, Integer> vertexDistance;
    Map<String, String> vertexParent;


    BellmanFordSSSP(){

        vertices = new LinkedList<String>();
        edgeList = new LinkedList<Edge>();
    }

    void insertVertex(String vertex) {

        vertices.add(vertex);
    }

    void insertEdge(String vertex1, String vertex2, int edgeVal) {

        Edge edge = new Edge();

        edge.startVertex = vertex1;
        edge.endVertex = vertex2;
        edge.value = edgeVal;

        edgeList.add(edge);
    }


    public void getShortestPath(String sourceVertex) {

        vertexDistance = new HashMap<String, Integer>();
        vertexParent = new HashMap<String, String>();

       //Set the initial distance of every vertex to infinity
        for(String vertex : vertices) {
            vertexDistance.put(vertex, Integer.MAX_VALUE);
            vertexParent.put(vertex, null);
        }

        //Initialise the distance of source vertex to be 0
        vertexDistance.put(sourceVertex, 0);

        int V = vertices.size();

        for (int i = 0; i < V - 1 ; i++) {
            for (Edge edge : edgeList) {
                String u = edge.startVertex;
                String v = edge.endVertex;
                
                //relax the edge
                if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
                    vertexDistance.put(v, vertexDistance.get(u) + edge.value);
                    vertexParent.put(v, u);
                }
            }
        }

        //Relax all the edges again. If we are still getting a lesser distance then 
        //there is negative weight cycle in the graph. 
        for (Edge edge : edgeList) {
            String u = edge.startVertex;
            String v = edge.endVertex;
            if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
                System.out.println("The Graph contains negative weight cycle");
                return;
            }
        }
    }

    public void printShortestPath() {

        for (Map.Entry<String,Integer> entry : vertexDistance.entrySet()) {

            System.out.println("The shortest distance between a and "+entry.getKey()+" is "+entry.getValue());
        }
    }

    public static void main(String args[]){

        BellmanFordSSSP bellmanFordSSSP = new BellmanFordSSSP();

        // Adding vertices one by one

        bellmanFordSSSP.insertVertex("a");
        bellmanFordSSSP.insertVertex("b");
        bellmanFordSSSP.insertVertex("c");
        bellmanFordSSSP.insertVertex("d");
        bellmanFordSSSP.insertVertex("e");

        //Adding edges with values.

        bellmanFordSSSP.insertEdge("a", "b", 18);
        bellmanFordSSSP.insertEdge("a", "c", 2);
        bellmanFordSSSP.insertEdge("a", "d", 4);

        bellmanFordSSSP.insertEdge("c", "e", 1);

        bellmanFordSSSP.insertEdge("e", "b", 5);

        bellmanFordSSSP.insertEdge("d", "c", 12);
        bellmanFordSSSP.insertEdge("d", "e", 3);



        bellmanFordSSSP.getShortestPath("a");

        bellmanFordSSSP.printShortestPath();;
    }
}

Output :

The shortest distance between a and a is 0
The shortest distance between a and b is 8
The shortest distance between a and c is 2
The shortest distance between a and d is 4
The shortest distance between a and e is 3

Code explanation for Bellman Ford's Algorithm - Single Source Sortest path

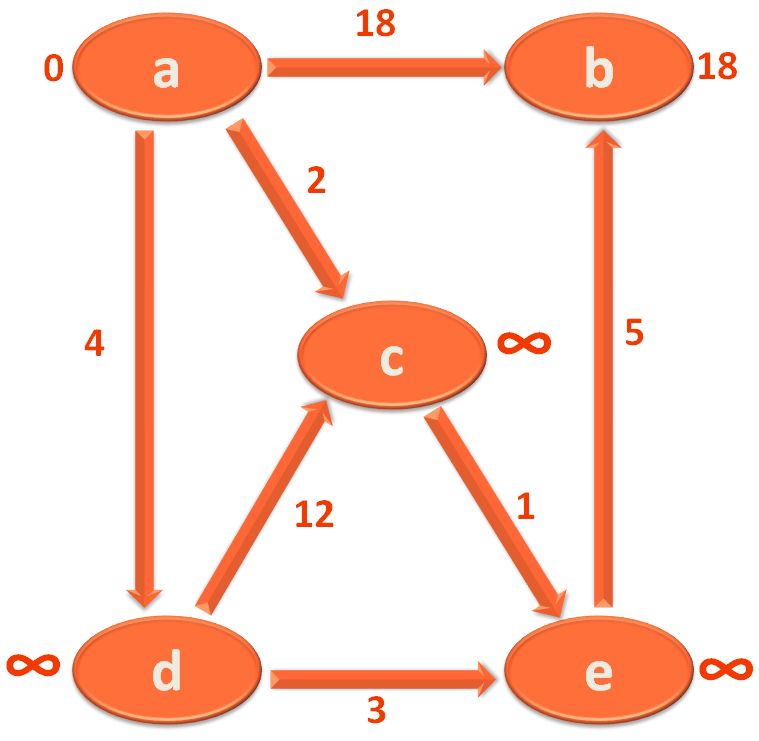
For explanation purpose we will be taking the below Graph :

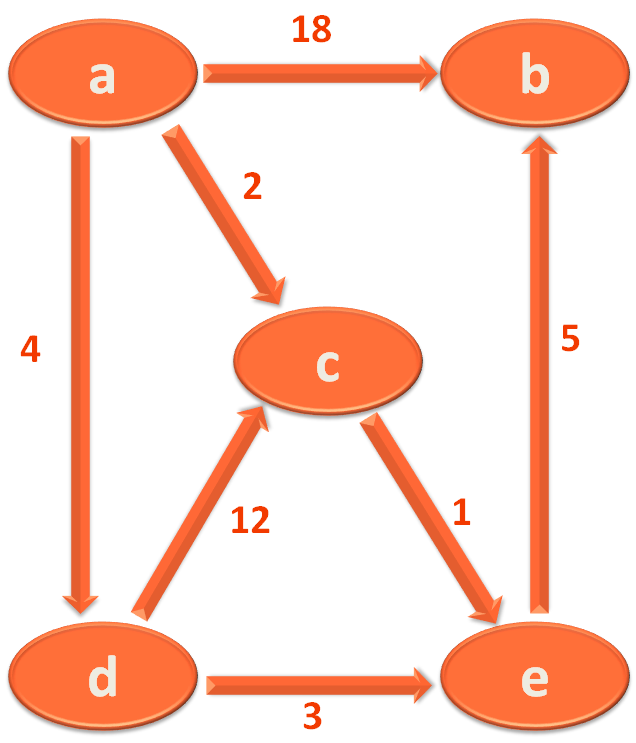
So, the first thing we will do is construct create a List,

LinkedList<String> vertices;

And store all the Vertices there,

bellmanFordSSSP.insertVertex("a");
bellmanFordSSSP.insertVertex("b");
bellmanFordSSSP.insertVertex("c");
bellmanFordSSSP.insertVertex("d");
bellmanFordSSSP.insertVertex("e");

The next thing we would do is, list out all the Edges.

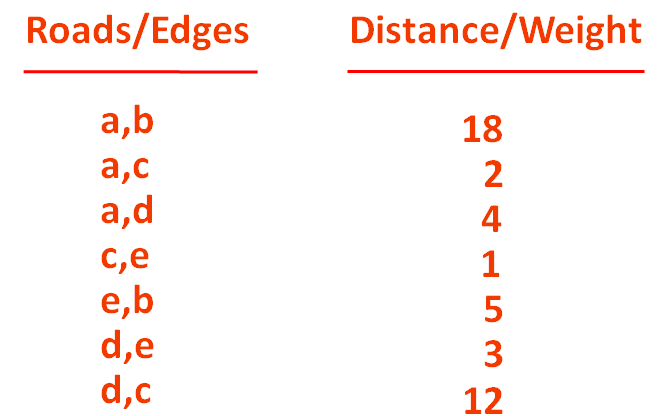
So, we would create a List,

LinkedList<Edge> edgeList;

And store all the Edges in the 'edgeList',

bellmanFordSSSP.insertEdge("a", "b", 18);
bellmanFordSSSP.insertEdge("a", "c", 2);
bellmanFordSSSP.insertEdge("a", "d", 4);

bellmanFordSSSP.insertEdge("c", "e", 1);

bellmanFordSSSP.insertEdge("e", "b", 5);

bellmanFordSSSP.insertEdge("d", "c", 12);
bellmanFordSSSP.insertEdge("d", "e", 3);

And we have the method 'insertEdge(...)' that initialises the Edges,

void insertEdge(String vertex1, String vertex2, int edgeVal) {

    Edge edge = new Edge();

    edge.startVertex = vertex1;
    edge.endVertex = vertex2;
    edge.value = edgeVal;

    edgeList.add(edge);
}

The 'insertEdge(...)' method is quite simple to understand. We already have the 'Edge' class :

class Edge {

    String startVertex;
    String endVertex;

    int value;
}

We have created an Edge object,

 Edge edge = new Edge();

And initialised the values,

edge.startVertex = vertex1;
edge.endVertex = vertex2;
edge.value = edgeVal;

Finally, added the 'edge' object to the List 'edgeList'.

edgeList.add(edge);

And one by one, we add all the edges to the List edgeList. And, finally the List 'edgeList' has all the Edges in it.

Now, since we have all the edges in the List 'edgeList'. It is time for us to call the method 'getShortestPath(...)' by passing the start vertex 'a' to it.

bellmanFordSSSP.getShortestPath("a");

Explanation of 'void getShortestPath(String sourceVertex)' method :

public void getShortestPath(String sourceVertex) {

    vertexDistance = new HashMap<String, Integer>();
    vertexParent = new HashMap<String, String>();

    //Set the initial distance of every vertex to infinity
    for(String vertex : vertices) {
        vertexDistance.put(vertex, Integer.MAX_VALUE);
        vertexParent.put(vertex, null);
    }

    //Initialise the distance of source vertex to be 0
    vertexDistance.put(sourceVertex, 0);

    int V = vertices.size();

    for (int i = 0; i < V - 1 ; i++) {
        for (Edge edge : edgeList) {
            String u = edge.startVertex;
            String v = edge.endVertex;
                
            //relax the edge
            if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
                vertexDistance.put(v, vertexDistance.get(u) + edge.value);
                vertexParent.put(v, u);
            }
        }
    }

    //Relax all the edges again. If we are still getting a lesser distance then 
    //there is negative weight cycle in the graph. 
    for (Edge edge : edgeList) {
        String u = edge.startVertex;
        String v = edge.endVertex;
        if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
            System.out.println("The Graph contains negative weight cycle");
            return;
        }
    }
}

So, what we have done is, created two Maps.

The first Map 'vertexDistance' stores vertex as key and the value as the one we were marking each vertex with.

vertexDistance = new HashMap<String, Integer>();

In simple words,

If we take the example of the Edge a,b with value 18.

The Vertex 'a' is marked with 0 and Vertex 'b' is marked with 18.

So, the Map 'vertexDistance' stores Vertex 'a' as key and 0 as value.

Similarly, the Map 'vertexDistance' stores Vertex 'b' as key and 18 as value.

Quite clear !

Now, let us see the second Map,

vertexParent = new HashMap<String, String>();

The second Map 'vertexParent' stores vertex as key and the value as its immediate source vertex.

If we take the same example of the Edge a,b with value 18.

So, the Map 'vertexParent' stores Vertex 'b' as key and vertex 'a' as value.

Similarly, if we take the example of the Edge d,e with length 3.

Then the Map 'vertexParent' stores Vertex 'e' as key and vertex 'd' as value.

Fair enough !

So, the next thing we will do is, mark all the Vertices with '∞' except the starting vertex 'a', which should be marked with '0'.

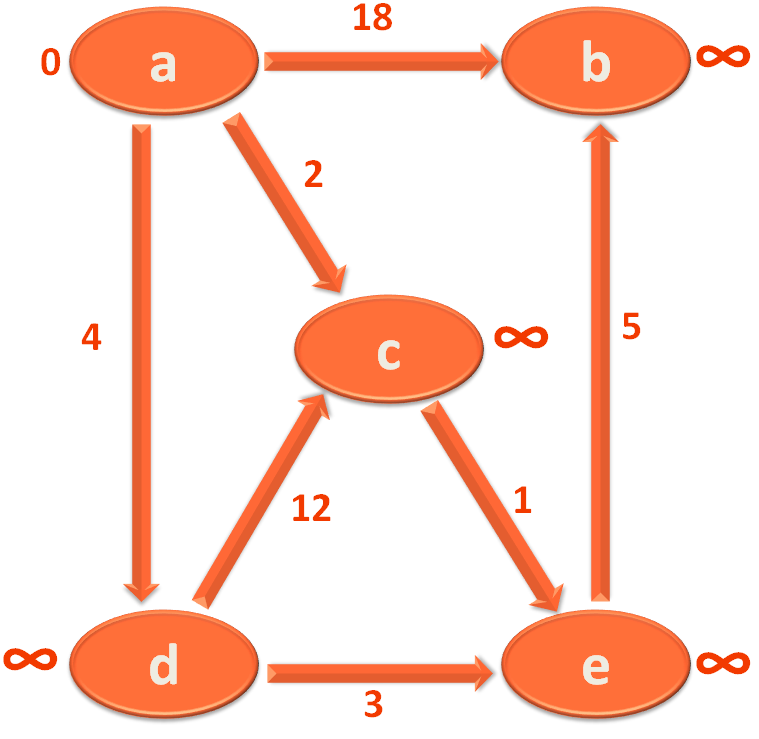
And to do this we will take all the Vertices one by one and put in the Map 'vertexDistance' and initialise the value of each Vertex to '∞' or 'Integer.Max_value'.

And at the same time, take the vertices and put in the Map 'vertexParent' and initialise the value of each Vertex to null.

for(String vertex : vertices) {
    vertexDistance.put(vertex, Integer.MAX_VALUE);
    vertexParent.put(vertex, null);
}

vertexDistance.put(sourceVertex, 0);

Then comes the 'for' loop where in each iteration the marking and relaxing process takes place. And we iterate it V-1 times. Where V is the number of Vertices.

for (int i = 0; i < V - 1 ; i++) {
    for (Edge edge : edgeList) {
        String u = edge.startVertex;
        String v = edge.endVertex;
                
        //Relax the edge
        if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
            vertexDistance.put(v, vertexDistance.get(u) + edge.value);
            vertexParent.put(v, u);
        }
    }
}

The above 'for' loop is quite simple.

As said we iterate the 'for' loop V-1 times.

for (int i = 0; i < V - 1 ; i++) {

There is a nested 'for' loop inside it. Which collects all the edges from the List 'edgeList',

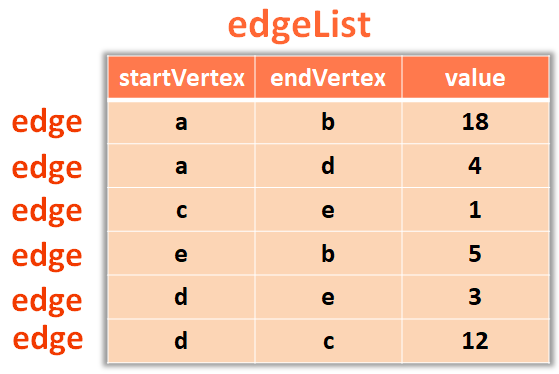
And iterates through all the edges from the List 'edgeList', one by one.

for (Edge edge : edgeList) {
    String u = edge.startVertex;
    String v = edge.endVertex;
                
    //Relax the edge
    if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
        vertexDistance.put(v, vertexDistance.get(u) + edge.value);
        vertexParent.put(v, u);
    }
}

So, in the above nested 'for' loop, it takes the the first edge,

And the 'startVertex' i.e. 'a' is put in a String 'u',

String u = edge.startVertex;

and the 'endVertex' i.e. 'b' is put in a String 'v'.

String v = edge.endVertex;

So, 'u' would contain vertex 'a' and 'v' would contain the vertex 'b'.

Next, we come across the line that has the 'if' statement. Where the actual relaxation process takes place.

if (vertexDistance.get(u) + edge.value  < vertexDistance.get(v)) {
    vertexDistance.put(v, vertexDistance.get(u) + edge.value);
    vertexParent.put(v, u);
}

So, if we have a closer look at the 'if' statement,

if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {

The 'if' statement has,

vertexDistance.get(u)
edge.value
vertexDistance.get(v)

The 'vertexDistance' is a Map that has the Key as Vertex name and value as the 'value' marked with the current vertex.

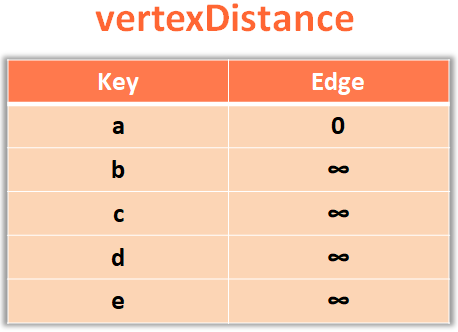
Currently all the vertices are marked with '∞'. Except the starting vertex 'a' which is marked with '0'.

Now, let us relook the condition inside 'if' statement.

if (vertexDistance.get(u) + edge.value < vertexDistance.get(v))

The variable 'u' has the value 'a' inside it.

So, 'vertexDistance.get(u)' gives us 0(As the value associated with the key 'a' is 0 in 'vertexDistance' Map).

Similarly, vertexDistance.get(v) gives us '∞'(As the value associated with the key 'b' is '∞' in 'vertexDistance' Map).

And 'edge.value' gives us 18 (Because the current edge we are dealing with is a,b with value '18').

Now, if we see the add operation,

vertexDistance.get(u) + edge.value

It would be '0 + 18', i.e. 18

and check if the added value 18 is less than 'vertexDistance.get(v)' (i.e. ∞).

if (vertexDistance.get(u) + edge.value < vertexDistance.get(v))

And obviously, 18 is less than ∞.

So, we get into the 'if' block and relax/replace the new added value 'vertexDistance.get(u) + edge.value' i.e. 18 to the value of vertex 'b'

vertexDistance.put(v, vertexDistance.get(u) + edge.value);

At the same time change the parent of 'b' to 'a' in 'vertexParent'.

Note : In the Map 'vertexDistance', we are storing the vertex and its marked distance (i.e. Vertex 'b' and 18). And to track the immediate parent of vertex 'b' we are using the Map 'vertexParent'. Where we are storing the immediate parent of 'b' in parallel.

Same way we have to take the next edge and continue with the 'for' loop.

for (Edge edge : edgeList) {
    String u = edge.startVertex;
    String v = edge.endVertex;
                
    //Relax the edge
    if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
        vertexDistance.put(v, vertexDistance.get(u) + edge.value);
        vertexParent.put(v, u);
    }
}

So, the next edge in the List 'edgeList' is,

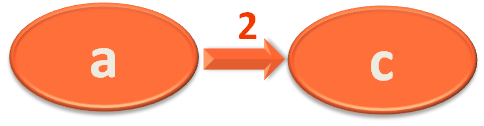
Similarly we take the 'startVertex' and 'endVertex' of edge object in 'u' and 'v'.

So, right now 'u' has 'a' and 'v' has 'c'.

Next, we add the current value of vertex 'a' in 'vertexDistance' (i.e. 0) and the current value of the edge (i.e. 2)

vertexDistance.get(u) + edge.value

and check if the added value(i.e. 2) is less than the value of vertex 'd' in 'vertexDistance' (i.e. ∞).

if (vertexDistance.get(u) + edge.value < vertexDistance.get(v))

And obviously, 2 is less than ∞.

So, we get into the 'if' block and relax/replace the new added value 'vertexDistance.get(u) + edge.value' i.e. 2 to the value of vertex 'c'

vertexDistance.put(v, vertexDistance.get(u) + edge.value);

At the same time change the parent of 'c' to 'a' in 'vertexParent'.

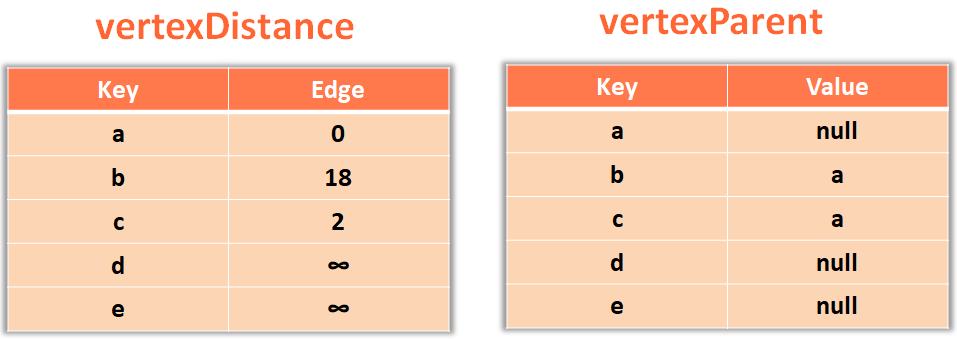
And if we continue the same process, we get the Stortest Path from source vertex 'a' to all the other Vertices.

Well ! We are not done yet.

What if there is a negative weight cycle ?

And we have the code to deal with negative weight cycle.

//Relax all the edges again. If we are still getting a lesser distance then 
//there is negative weight cycle in the graph. 
for (Edge edge : edgeList) {
    String u = edge.startVertex;
    String v = edge.endVertex;
    if (vertexDistance.get(u) + edge.value < vertexDistance.get(v)) {
        System.out.println("The Graph contains negative weight cycle");
        return;
    }
}

The above code is quite simple to understand.

We usually continue iterating (V-1) times. Where V is the number of vertices. In this case we iterate V times. And if the weight reduces then there is a negative weight cycle.

Explanation of the Node class in the above code

Since we are running a nested 'for' loop.

So, the running time is : O(VE)

Where V is the number of Vertices And E is the number of Edges.

❮❮ PREV