KRUSKAL's ALGORITHM - MINIMUM SPANNING TREE CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

import java.util.*;

class Node {

    String data;
    int rank;
    Node parent;
}

class Edge implements Comparable<Edge>{

    String startVertex;
    String endVertex;

    int value;
    
    @Override
    public int compareTo(Edge edge) {
        return value - edge.value;
    }
}

public class KruskalMST {

    Map<String, Node> map = new HashMap< >();

    List<String> vertices = new LinkedList< >();

    List<Edge> edgeList = new LinkedList< >();

    void insertVertex(String vertex) {

        vertices.add(vertex);
    }

    void insertEdge(String vertex1, String vertex2, int edgeVal) {

        Edge edge = new Edge();

        edge.startVertex = vertex1;
        edge.endVertex = vertex2;
        edge.value = edgeVal;

        edgeList.add(edge);
    }

    // Create groups with only one vertex.
    public void createSet(String data){

        Node node = new Node();
        node.data = data;
        node.rank = 0;
        node.parent = node;
        map.put(data, node);
    }

    //Combines two groups into one. Does union by rank.
    public void union(String vertex1, String vertex2){

        Node node1 = map.get(vertex1);
        Node node2 = map.get(vertex2);

        Node parent1 = findSet(node1);
        Node parent2 = findSet(node2);

        //If they are in the same group, do nothing.
        if(parent1.data == parent2.data) {

            return;
        }
        //Else whose rank is higher becomes parent of other.
        if (parent1.rank <= parent2.rank) {

            //Increment rank only if both sets have same rank.
            parent1.rank = (parent1.rank == parent2.rank) ? parent1.rank + 1 : parent1.rank;
            parent2.parent = parent1;
        }
        else {

            parent1.parent = parent2;
        }
    }

    // Find the representative of this set

    public String findSet(String data){

        return findSet(map.get(data)).data;
    }

    // Finds the leader/representative recursivly and does PATH COMPRESSION as well.
    private Node findSet(Node node){

        Node parent = node.parent;
        if (parent == node) {

            return parent;
        }
        node.parent = findSet(node.parent);
        return node.parent;
    }


    // Find Minimum Spanning Tree using Kruskal's Algorithm.
    public List<Edge> createMST() {

        //Sort all edges in Ascending order.
        Collections.sort(edgeList);
        KruskalMST kruskalMST = new KruskalMST();

        //Create as many groups as the total vertices.
        for (String vertex : vertices) {

            kruskalMST.createSet(vertex);
        }

        List<Edge> resultEdge = new ArrayList< >();

        for (Edge edge : edgeList) {

            //Get the sets of two vertices of the edge.
            String root1 = kruskalMST.findSet(edge.startVertex);
            String root2 = kruskalMST.findSet(edge.endVertex);

            //check if the vertices are on the same or different set.
            //If vertices are in the same set then ignore the edge.
            if (root1 == root2) {

                continue;
            }
            else {

                // If vertices are in different sets then add the edge to result and union 
                // these two sets into one.
                
                resultEdge.add(edge);
                kruskalMST.union(edge.startVertex, edge.endVertex);
            }
        }
        return resultEdge;
    }

    public static void main(String[] args) {

        KruskalMST kruskalMST = new KruskalMST();



        // Adding vertices one by one

        kruskalMST.insertVertex("a");
        kruskalMST.insertVertex("b");
        kruskalMST.insertVertex("c");
        kruskalMST.insertVertex("d");
        kruskalMST.insertVertex("e");

        //Adding edges with values.

        kruskalMST.insertEdge("a", "b", 1);
        kruskalMST.insertEdge("b", "e", 8);
        kruskalMST.insertEdge("e", "d", 3);
        kruskalMST.insertEdge("d", "a", 4);
        kruskalMST.insertEdge("a", "c", 5);
        kruskalMST.insertEdge("c", "e", 9);
        kruskalMST.insertEdge("c", "d", 12);

        List<Edge> mstList = kruskalMST.createMST();

        for (Edge edge : mstList) {

            System.out.println("The edge : "+edge.startVertex+" -- "+edge.endVertex+" with value : "+edge.value);
        }

    }

}

Output :

The edge : a -- b with value : 1
The edge : e -- d with value : 3
The edge : d -- a with value : 4
The edge : a -- c with value : 5

Brief recap of Kruskal's Algorithm for Minimum Spanning Tree

Note : We have used 'Union by Rank' and 'Path Compression' technique. You can have a look at it. If not, not worries. We will explain in brief.

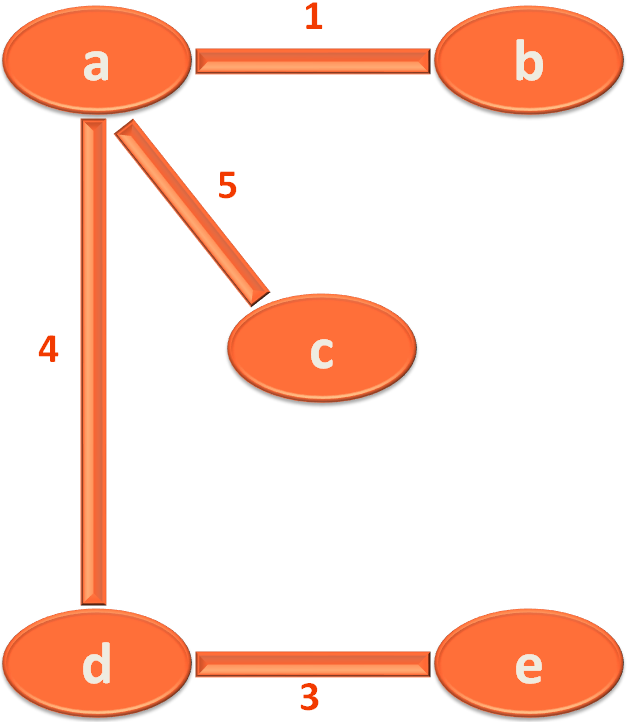
So, we will be dealing with the below Graph,

First thing we do is, sort all the edges in ascending order.
Then, create individual groups for each vertices and initialise with rank 0.

1st Group - {a} --- rank 0
2nd Group - {b} --- rank 0
3rd Group - {c} --- rank 0
4th Group - {d} --- rank 0
5th Group - {e} --- rank 0

Now, we need to elect a leader for each group. And, since there is only one vertex in each group, the individual group member will be marked as leader of their group.

Say for example,

'a' is the leader of group 1, 'b' is leader of group 2 and so on.

And leaders are given a superior 'rank' 0.
Next, take the sorted edges, one by one, connect them and increment the leader rank by 1.

For Example :

The first sorted edge is a,b. So, we connect 'a' and 'b',

a --- b

Then take 'a' from group 1 and 'b' from group 2.

1st Group - {a} --- rank 0
2nd Group - {b} --- rank 0

And, combine 'a' and 'b' in group 1.

1st Group - {a,b}

Now, it is time to elect a leader for 1st Group.

And 'a' was the leader/representative of group 1 and now, 'b' came to group 1.

So, we make 'b' the child of 'a'. And since 'a' is the leader, 'a' is given 'rank' 1.

And the same steps are repeated.

This feature of combining two groups and ranking them is Union by Rank.

Explanation of the Node class in the above code

In the above code, we have a class called 'Node'. Which looks a little different.

class Node {

    String data;
    int rank;
    Node parent;
}

You can think of the 'Node' class as a representation of a Vertex.

And how is that so ?

Just think, a vertex should have a rank and its name. And so we have

String data
int rank

But the only mystery is, what is 'Node parent'?

A 'Node' object inside a 'Node' class ! Looks Strange ! Right ?

It is like a connection, we are trying to establish between Vertices.

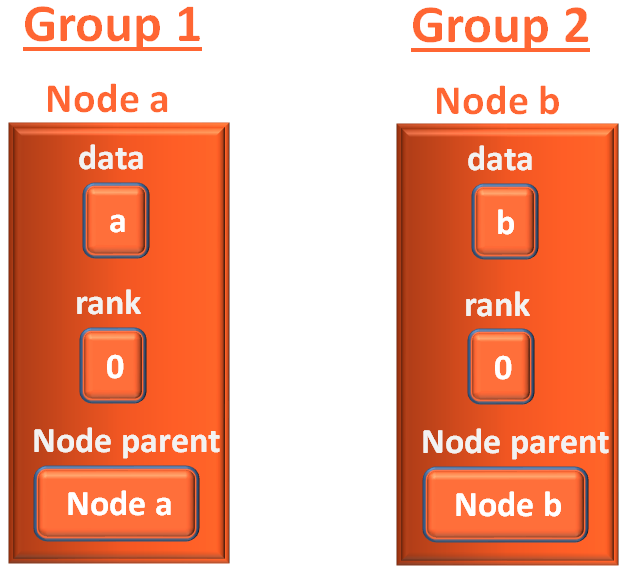
So, when the vertices are created for the first time, they should the leader of their group and off course they should be their parent.

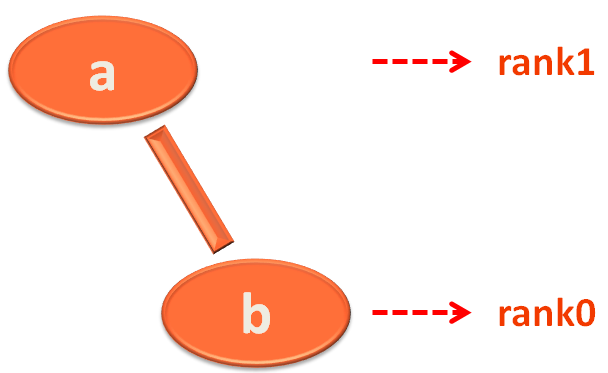
Say for example when vertex 'a' and 'b' is created, 'a' is in group 1 and 'b' is in group 2.

'Node parent' for vertex 'b' is Node b (Since vertex 'b' is the leader of group 2).

And 'Node parent' for vertex 'a' is Node a (Since vertex 'a' is the leader of group 1).

Next, when b is put into group 1, the leader of group 1 is 'a'.

So, vertex 'b' is a child of 'a'.

And 'Node parent' of b is 'Node a' now.

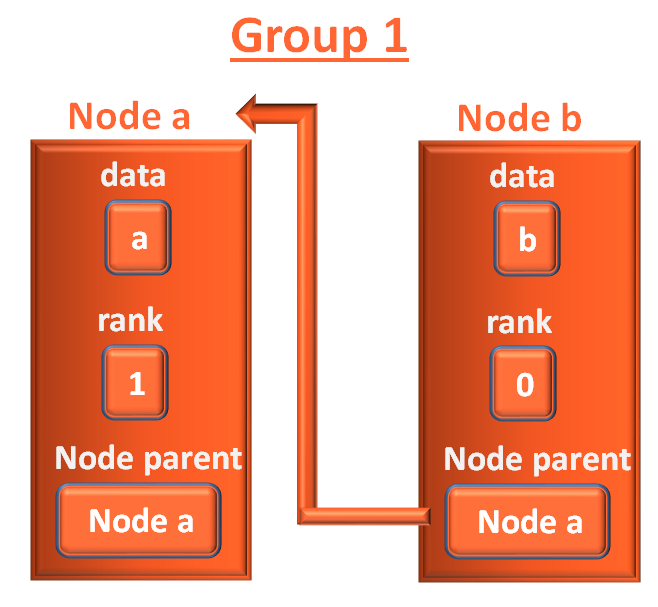
The vertex 'a' is named as Node a and vetex 'b' is named as Node b. We have seen how the connection is established.

Explanation of the Edge class in the above code

As we have seen the 'Node' class is used to store the contents of the Vertices.

Similarly, the 'Edge' class is used to store the contents of the Edges.

class Edge implements Comparable<Edge>{

    String startVertex;
    String endVertex;

    int value;
    
    @Override
    public int compareTo(Edge edge) {
        return value - edge.value;
    }
}

The 'Edge' class has three attributes,

- startVertex
- endVertex
- value

The above one is the example of an edge that has,

startVertex = a
endVertex = b
value = 1

And we have used 'Comparable' in the 'Edge' class, to sort the 'Edge' objects by values.

@Override
public int compareTo(Edge edge) {
    return value - edge.value;
}

Code explanation of Kruskal's Algorithm for Minimum Spanning Tree

So, firstly we construct the graph by adding the vertices.

 // Adding vertices one by one

kruskalMST.insertVertex("a");
kruskalMST.insertVertex("b");
kruskalMST.insertVertex("c");
kruskalMST.insertVertex("d");
kruskalMST.insertVertex("e");

Then adding the edges with its values,

 //Adding edges with values.

kruskalMST.insertEdge("a", "b", 1);
kruskalMST.insertEdge("b", "e", 8);
kruskalMST.insertEdge("e", "d", 3);
kruskalMST.insertEdge("d", "a", 4);
kruskalMST.insertEdge("a", "c", 5);
kruskalMST.insertEdge("c", "e", 9);
kruskalMST.insertEdge("c", "d", 12);

Then we call the 'createMST()' method to construct Minimum Spanning Tree using Kruskal's Algorithm.

 List<Edge> mstList = kruskalMST.createMST();

Explanation of 'public List<Edge> createMST()' method

public List<Edge> createMST() {

    //Sort all edges in Ascending order.
    Collections.sort(edgeList);
    KruskalMST kruskalMST = new KruskalMST();

    //Create individual groups for each vertex.
    for (String vertex : vertices) {

        kruskalMST.createSet(vertex);
    }

    List<Edge> resultEdge = new ArrayList<>();

    for (Edge edge : edgeList) {

        //Get the sets of two vertices of the edge.
        String root1 = kruskalMST.findSet(edge.startVertex);
        String root2 = kruskalMST.findSet(edge.endVertex);

        //check if the vertices are on the same or different set.
        //If vertices are in the same set then ignore the edge.
        if (root1 == root2) {

            continue;
        }
        else {

            // If vertices are in different sets then add the edge to result and union 
            // these two sets into one.
                
            resultEdge.add(edge);
            kruskalMST.union(edge.startVertex, edge.endVertex);
        }
    }
    return resultEdge;
}

As we know, the first task is to sort the Edges,

Collections.sort(edgeList);

The next task would be, to create individual groups for each Vertex using the 'createSet()' method.

for (String vertex : vertices) {

    kruskalMST.createSet(vertex);
}

As we know 'vertices'

List<String> vertices = new LinkedList<>();

contains the List of Vertices. So, we take the vertices one by one using the for each loop and call the 'creteSet()' method.

kruskalMST.createSet(vertex);

Explanation of 'public void createSet(String data)' method

public void createSet(String data){

    Node node = new Node();
    node.data = data;
    node.rank = 0;
    node.parent = node;
    map.put(data, node);
}

The parameter 'String data' contains the vertex(Say 'a' for vertex 'a').

So, we create a Node object to hold the actual vertex(Say value 'a' for vertex 'a')

node.data = data;

the rank of the vertex.

node.rank = 0;

'rank' is initialised to '0' because initially all the vertices would be the leader of their group and the leader is ranked '0'.

The next line is extremely important,

node.parent = node;

Now since, 'vertex a' is the leader of their group. 'node.parent' is 'vertex a' itself.

Below is the example of 'vertex a'.

Then we put the created 'node' in the 'map',

Map<String, Node> map = new HashMap<>();

With the key as the value of vertex( 'a' in this case) and value as the created 'node'.

 map.put(data, node);

All the Nodes/vertices are created in the same way and put in the 'map'.

Let us come back to the 'createMST()' method again,

And since we got all the groups created.

Now, it's time for us to implement the actual logic.

And we have declared 'resultEdge' List that will store all the edges included in the Minimum Spanning Tree.

 List<Edge> resultEdge = new ArrayList<>();

Now, we know that the List 'edgeList',

List<Edge> edgeList = new LinkedList<>();

Contains the List of all the edges in the Graph(Off course Sorted in ascending order done earlier).

And what will will do is take List 'edgeList' one by one and try constructing the Minimum Spanning Tree.

for (Edge edge : edgeList) {

    //Get the sets of two vertices of the edge.
    String root1 = kruskalMST.findSet(edge.startVertex);
    String root2 = kruskalMST.findSet(edge.endVertex);

    //check if the vertices are on the same or different set.
    //If vertices are in the same set then ignore the edge.
    if (root1 == root2) {

        continue;
    }
    else {

        // If vertices are in different sets then add the edge to result and union 
        // these two sets into one.
                
        resultEdge.add(edge);
        kruskalMST.union(edge.startVertex, edge.endVertex);
    }
}

So, the 'for each' loop, takes the sorted edges one by one,

for (Edge edge : edgeList)

And the first thing it does is, tries to find the leader of each vertex using the 'findSet()' method,

	String root1 = kruskalMST.findSet(edge.startVertex);
	
 String root2 = kruskalMST.findSet(edge.endVertex);

Explanation of 'public String findSet(String data)' method

public String findSet(String data){

    return findSet(map.get(data)).data;
}

Now, the cool thing to note is, the return statement,

return findSet(map.get(data)).data;

Calls another 'findSet(...)' method.

Sounds Interesting or Strange?

Let's dive in,

map.get(data) from the return statement,

return findSet(map.get(data)).data;

gives us a Node object.

How ?

Because, we have seen 'map' holds Key as the Vertex name (Say 'a') and its Node as value.

And if we pass the value 'a' to the Map,

map.get("a")

We get the Node object of 'a'.

So, this time we will be calling the 'findSet(...)' method, that accepts Node as parameter.

And luckily, we have the 'private Node findSet(Node node)' method.

Explanation of 'private Node findSet(Node node)' method

private Node findSet(Node node){

    Node parent = node.parent;
    if (parent == node) {

        return parent;
    }
    node.parent = findSet(node.parent);
    return node.parent;
}

So, in the first line, we have created a Node variable called 'parent' and initialised the 'parent' variable with the 'parent' from the parameter 'Node node'.

Say, we have passed Node 'a' and the parent of Node a is Node a(Because Node a is the leader).

Node parent = node.parent;

Then we check if the Node 'parent' is equal to the node from parameter 'Node node'.

if (parent == node) {

    return parent;
}

In this case Node 'parent' and Node 'node' are equal.

So, the Node 'parent' is returned.

But ! Yes there is a BUT.

Say, the node 'b' was passed, when it was a child of 'a'.

Now, let us relook the steps for Node 'b',

Node parent = node.parent;

So, Node 'parent' would be Node 'a'.

And Node 'parent' would be holding the Node 'a'.

Then we check if the Node 'parent' is equal to the node from parameter 'Node node'.

if (parent == node) {

    return parent;
}

And 'if' condition is not satisfied as

Node 'parent' is holding Node 'a' and 'node' is holding Node 'b'.

Fair enough !

Then we go to the next line, where 'findSet(Node node)' method is called recursively,

node.parent = findSet(node.parent);

Until it finds the parent and finally 'node.parent' is returned.

return node.parent;

So, let us come back to 'createMST()' method again.

Let us take the example of edge

String root1 = kruskalMST.findSet(edge.startVertex);
String root2 = kruskalMST.findSet(edge.endVertex);

Where, 'edge.startVertex' is 'a' and 'edge.endVertex' is 'b'.

And we found the parent of 'a' is 'a' itself and parent of 'b' is 'b'.

So,

String root1 = "a"

and

String root2 = "b"

And, if we see the code again,

for (Edge edge : edgeList) {

    //Get the sets of two vertices of the edge.
    String root1 = kruskalMST.findSet(edge.startVertex);
    String root2 = kruskalMST.findSet(edge.endVertex);

    //check if the vertices are on the same or different set.
    //If vertices are in the same set then ignore the edge.
    if (root1 == root2) {

        continue;
    }
    else {

        // If vertices are in different sets then add the edge to result and union 
        // these two sets into one.
                
        resultEdge.add(edge);
        kruskalMST.union(edge.startVertex, edge.endVertex);
    }
}

There is this 'if' statement that checks,

if (root1 == root2)

But in this case root1 is 'a' and root2 is 'b'.

So, we come to the else part.

else {

    // If vertices are in different sets then add the edge to result and union 
    // these two sets into one.
                
    resultEdge.add(edge);
    kruskalMST.union(edge.startVertex, edge.endVertex);
}

Now since, we are in the 'else' part. This edge,

must be included in the Minimum Spanning Tree.

resultEdge.add(edge);

And thus, we have added it to the 'resultEdge' list.

So, the next task would be to combine 'a' and 'b' in the same group.

kruskalMST.union(edge.startVertex, edge.endVertex);

And this task of combining is done by the 'union(...)' method.

Explanation of 'public void union(String vertex1, String vertex2)' method

public void union(String vertex1, String vertex2){

    Node node1 = map.get(vertex1);
    Node node2 = map.get(vertex2);

    Node parent1 = findSet(node1);
    Node parent2 = findSet(node2);

    //If they are in the same group, do nothing.
    if(parent1.data == parent2.data) {

        return;
    }
    //Else whose rank is higher becomes parent of other.
    if (parent1.rank <= parent2.rank) {

        //Increment rank only if both sets have same rank.
        parent1.rank = (parent1.rank == parent2.rank) ? parent1.rank + 1 : parent1.rank;
        parent2.parent = parent1;
    }
    else {

        parent1.parent = parent2;
    }
}

Let us take the example of

to explain the 'union(...)' method.

 Node node1 = map.get(vertex1);
 Node node2 = map.get(vertex2);

And

node2 will have the contents of Node b and node1 will have the contents of Node a.

In the next two lines,

 Node parent1 = findSet(node1);
 Node parent2 = findSet(node2);

We try to find the parents/leaders of node1 and node2 using 'findSet(Node node)' method which we have already seen.

And in this case, the parent of 'a' is 'a' and the parent of 'b' is 'b'.

Next, we check, if both the parent of the vertices are equal or not,

 if(parent1.data == parent2.data) {

    return;  
}

If both the parents are equal, we do nothing.

But in this case, they are not equal as

parent1.data = "a"

and

parent2.data = "b"

So, we come to the next 'if' statement.

 if (parent1.rank <= parent2.rank) {

    //Increment rank only if both sets have same rank.
    parent1.rank = (parent1.rank == parent2.rank) ? parent1.rank + 1 : parent1.rank;
    parent2.parent = parent1;
}
else {

    parent1.parent = parent2;
}

In the 'if' statement, we check if parent1.rank is less than or equal to parent2.rank.

if (parent1.rank <= parent2.rank)

And in this case,

parent1.rank and parent2.rank has the same rank i.e. 0 (From the above diagram).

And in the next line,

parent1.rank = (parent1.rank == parent2.rank) ? parent1.rank + 1 : parent1.rank;

We increment the 'parent1.rank' only if 'parent1.rank' is equal to 'parent2.rank'.

And in this case 'parent1.rank' is equal to 'parent2.rank',

So, we increment parent1.rank by 1.

parent1.rank + 1

And parent1.rank becomes,

parent1.rank = 1

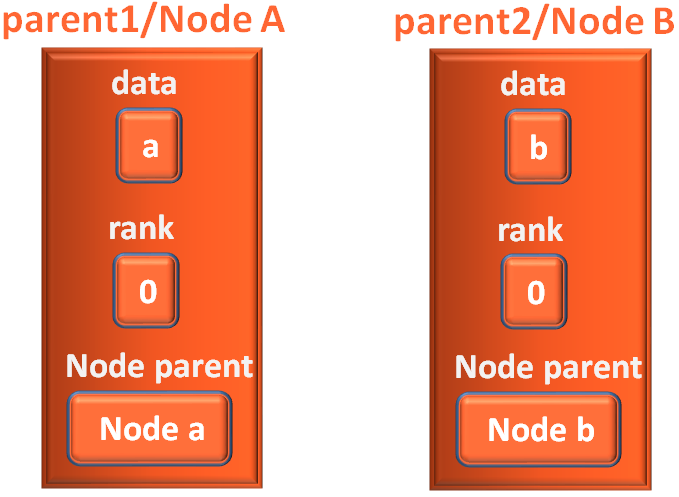
Then, we initialise parent2.parent with parent1.

parent2.parent = parent1;

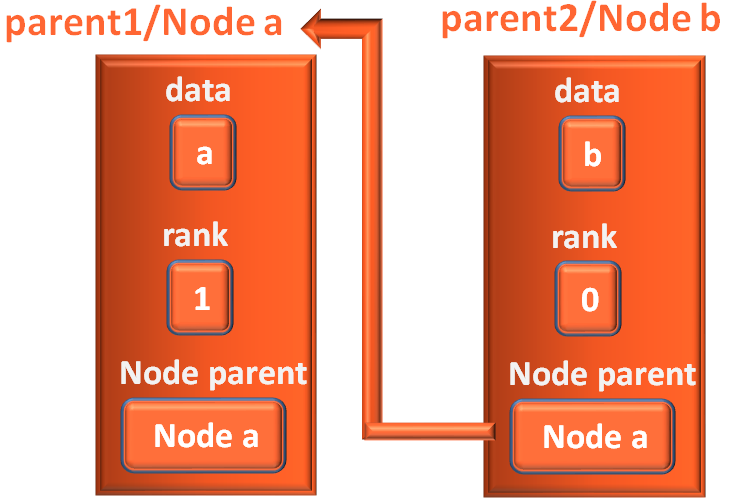
And we can see that the connection between a and b is established,

And continuing this way, we get the Minimum Spanning Tree,

❮❮ PREV NEXT ❯❯