<html>
<body>
<script>
class Node {
constructor(value) {
this.data = value
this.left = null
this.right = null
}
}
function searchNode(root, key) {
if(root == null)
return null;
if(root.data == key)
return root
else if(root.data < key)
return searchNode(root.right, key)
else
return searchNode(root.left, key)
}
function search(key) {
return searchNode(root,key)
}
function insertNode(root, key) {
if (root == null) {
root = new Node(key)
return root
}
if (key < root.data)
root.left = insertNode(root.left, key)
else if (key > root.data)
root.right = insertNode(root.right, key)
return root
}
function insert(key) {
root = insertNode(root, key)
}
function inOrderNode(root) {
if (root != null) {
inOrderNode(root.left)
document.write(root.data, " ")
inOrderNode(root.right)
}
}
function inOrder() {
inOrderNode(root)
}
function deleteNode(root, key) {
if (root == null)
return root
if (key < root.data)
root.left = deleteNode(root.left, key)
else if (key > root.data)
root.right = deleteNode(root.right, key)
else {
if (root.left == null)
return root.right
else if (root.right == null)
return root.left
root.data = minValue(root.right);
root.right = deleteNode(root.right, root.data)
}
return root
}
function customDelete(key) {
root = deleteNode(root, key)
}
function minValue(root) {
var min = root.data
while (root.left != null) {
min = root.left.data
root = root.left
}
return min
}
root = null
insert(16)
insert(10)
insert(25)
insert(13)
insert(18)
document.write("Inorder traversal: </br>")
inOrder()
searchedRes = search(5)
if (searchedRes == null)
document.write("</br></br>The number 5 is not present in the BST </br>")
else
document.write("</br>", searchedRes.data, " is present in the BST </br>")
document.write("</br>Let us delete the element 10 from the Binary Search Tree </br>")
customDelete(10)
document.write("</br> Inorder traversal after Deletion </br>")
inOrder()
insert(3)
document.write("</br> Inorder traversal after insertion of the new element 3 : </br>")
inOrder()
document.write()
</script>
</body>
</html>
So, we would be constructing the below Binary Search Tree :
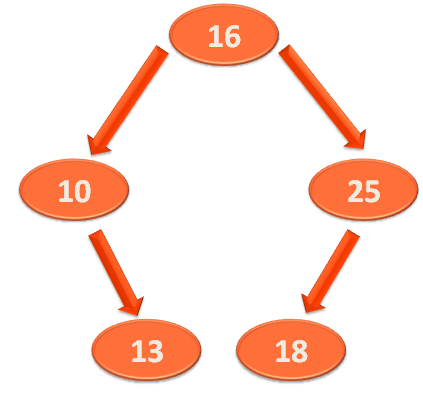
And we have the below methods :
Firstly, we would be constructing the above Binary Search Tree, with the help of insert method..
insert(16)
So, we pass the element 16 to the insert(...) method.
And the below insert(...) method with one argument is called.
function insert(key) {
root = insertNode(root, key)
}Initially, the variable root is null as defined the constructor. Then we take the key i.e. 16 in this case. And pass the root and key to the insert method with two arguments.
function insertNode(root, key) {
if (root == null) {
root = new Node(key)
return root
}
if (key < root.data)
root.left = insertNode(root.left, key)
else if (key > root.data)
root.right = insertNode(root.right, key)
return root
}The first line checks if the root is null or not.
if (root == null) {
root = new Node(key)
return root
}And in this case root is null. So, we create a new Node object with the key i.e. 16.
Then assign it to the Node object root.
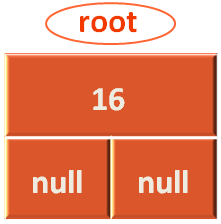
And return the Node root.
return root
In the next line we try to insert the element 10 in the Binary Search Tree using the insert(...) method.
insert(10)
And the insert(...) method is called.
And in the similar way we check,
if (key < root.data) root.left = insert(root.left, key) else if (key > root.data) root.right = insert(root.right, key)
If the key i.e. 10 is less than the root element root.data. The first condition matches.
if (key < root.data) root.left = insert(root.left, key)
And a recursive call is made to insert(...) method.
root.left = insert(root.left, key)
So, the method executes and returns the Node that contains 10, setting the value of root.left with this Node that contains 10.
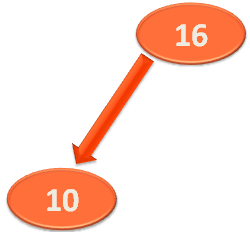
Similarly, all the elements are inserted using the insert(...) method.
insert(25) insert(13) insert(18)
And the below Binary Search Tree is formed,
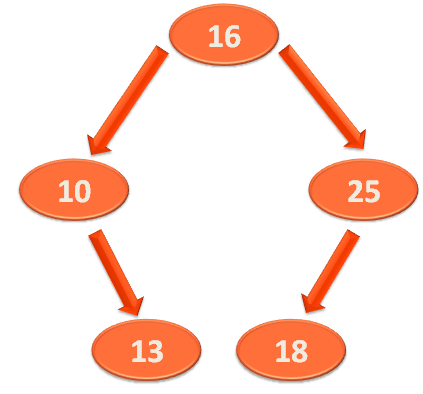
Then we use the inOrder() method to traverse the Binary Search Tree.
inOrder()
Next, we search, if the element 5 is present in the Binary Search Tree using the search(...)method.
searchedRes = search(5)
And the search(...) method with one argument is called.
function search(key) {
return searchNode(root,key)
}And the search(...) method with two arguments is called with the key element as 5(i.e The element to be searched).
function searchNode(root, key) {
if(root == null)
return null;
if(root.data == key)
return root
else if(root.data < key)
return searchNode(root.right, key)
else
return searchNode(root.left, key)
}So, there are a couple of if statements, where the first if statement checks if the root element is null or not.
if(root == null) return null
In this case the root element is 16. So, we go to the next if statement that checks if the key element 5 (i.e. The element to be searched), is equal to the root element or not.
if(root.data == key) return root
In this case the root element is 16 which is not equal to the element that needs to be searched.
So, the next if statement checks, if the element that needs to be searched(i.e. 5) is greater than the root element(i.e. 16) or not.
else if(root.data < key) return searchNode(root.right, key)
In this case 5 is less than 16. So, even this condition is not satisfied.
The logic behind this if statement is to check, if the element to be searched is greater than the root element or not. If the element to be searched, is greater than the root element then it should be on the right side of the tree and we are suppose to search there.
Now, since 5 is less than 16. We come to the final else statement. Which assumes that the element to be searched (i.e. 5) is less than the root element (i.e. 16) and must be on the left hand side.
else return search(root.left, key)
Now, in this else statement, a recursive call is made to the search(root.left, key) method.
So, the assumption is that the element 5 should be in the Left Sub-Tree.
And the Node search(Node root, int key) method is called again with the root as 10.

The same way all the if statements are executed and finally, the element 5 is not found in the Binary Search Tree.
Next, we try to delete the element 10 from the Binary Search Tree.
delete(10)
Calling the delete(...) method.
Similarly, in this case, delete(...) method with one argument is called,
function delete(key) {
root = deleteNode(root, key)
}And the deleteNode(...) method with two arguments is called.
function deleteNode(root, key) {
if (root == null)
return root
if (key < root.data)
root.left = deleteNode(root.left, key)
else if (key > root.data)
root.right = deleteNode(root.right, key)
else {
if (root.left == null)
return root.right
else if (root.right == null)
return root.left
root.data = minValue(root.right);
root.right = deleteNode(root.right, root.data)
}
return root
}So, we are trying to delete the element 10 from the Binary Search Tree. So, the key is 10 that we have passed to the delete(...) method.
The delete(...) method is almost same as the search(...) method.
In the search(...) method, we have located the element to be searched. Even in delete(...) method, we will locate the element first(The code is exactly same as the search(...) method). Then call the minValue(root.right) method
The minValue(...) method will find the inorder-successor. i.e. When we delete the element, we need to find a replacement of it, so that the Binary Search Tree properties should be intact.
Thus, we go to the Right Sub-Tree of the element to be deleted. And as we know the Right Sub-Tree contains all the elements that are greater than the root element. So, we have to find the smallest element from the Right Sub-Tree..
And, as we know the smallest element of the Right Sub-Tree resides on the leftmost leaf.
And that's exactly what we will find in function minValue(root) method.
function minValue(root) {
var min = root.data
while (root.left != null) {
min = root.left.data
root = root.left
}
return min
}