KOTLIN - DEPTH FIRST SEARCH CODE RECURSIVE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

We will be seeing the Recursive way for implementing Depth First Search (DFS).

In the Recursive code we don't have to create the stack and maintain it as kotlin will do the job for us. And the stack will be hidden from us.

DFS - Depth First Search code for Undirected Graph - Recursive approach

Example :

import java.util.LinkedList;

var vertices = LinkedList<String>();
var adjacencyList = LinkedList<LinkedList<String>>();
var visited: BooleanArray = booleanArrayOf();

class DFSRecursion {

    fun insertVertex(vertex: String) {

        vertices.add(vertex);
    }

    fun constructAdjacencyList(vtx: String, adjcVertex: String) {

        var vtxIndex = vertices.indexOf(vtx);

        adjacencyList.add(LinkedList<String>());
        adjacencyList.get(vtxIndex).add(adjcVertex);
    }

    fun depthFirstSearch(source: String){

        var sourceIndex = vertices.indexOf(source);

        visited[sourceIndex] = true;

        print("$source   ");

        var iter = adjacencyList.get(sourceIndex).iterator();
        while (iter.hasNext() ) {

            var str = iter.next();

            var i = vertices.indexOf(str);

            if (visited[i] == false) {

                visited[i] = true;
                depthFirstSearch(str);
            }
        }
    }
}

fun main(arr: Array<String>) {

    var V = 6;

    var dfsRecursion = DFSRecursion();

    visited = BooleanArray(V)

    adjacencyList = LinkedList<LinkedList<String>>();

    vertices = LinkedList();

    // Insert Vertices

    dfsRecursion.insertVertex("a");
    dfsRecursion.insertVertex("b");
    dfsRecursion.insertVertex("c");
    dfsRecursion.insertVertex("d");
    dfsRecursion.insertVertex("e");
    dfsRecursion.insertVertex("f");

    dfsRecursion.constructAdjacencyList("a", "c");
    dfsRecursion.constructAdjacencyList("a", "d");

    dfsRecursion.constructAdjacencyList("b", "d");
    dfsRecursion.constructAdjacencyList("b" ,"e");
    dfsRecursion.constructAdjacencyList("b" ,"c");

    dfsRecursion.constructAdjacencyList("c", "a");
    dfsRecursion.constructAdjacencyList("c", "b");
    dfsRecursion.constructAdjacencyList("c", "e");

    dfsRecursion.constructAdjacencyList("d", "a");
    dfsRecursion.constructAdjacencyList("d" ,"b");
    dfsRecursion.constructAdjacencyList("d", "e");
    dfsRecursion.constructAdjacencyList("d", "f");

    dfsRecursion.constructAdjacencyList("e", "b");
    dfsRecursion.constructAdjacencyList("e", "c");
    dfsRecursion.constructAdjacencyList("e", "d");
    dfsRecursion.constructAdjacencyList("e", "f");

    dfsRecursion.constructAdjacencyList("f", "d");
    dfsRecursion.constructAdjacencyList("f", "e");

    dfsRecursion.depthFirstSearch("a");
}

Output :

a c b d e f

We have implemented Depth First Search (DFS) on the below graph :

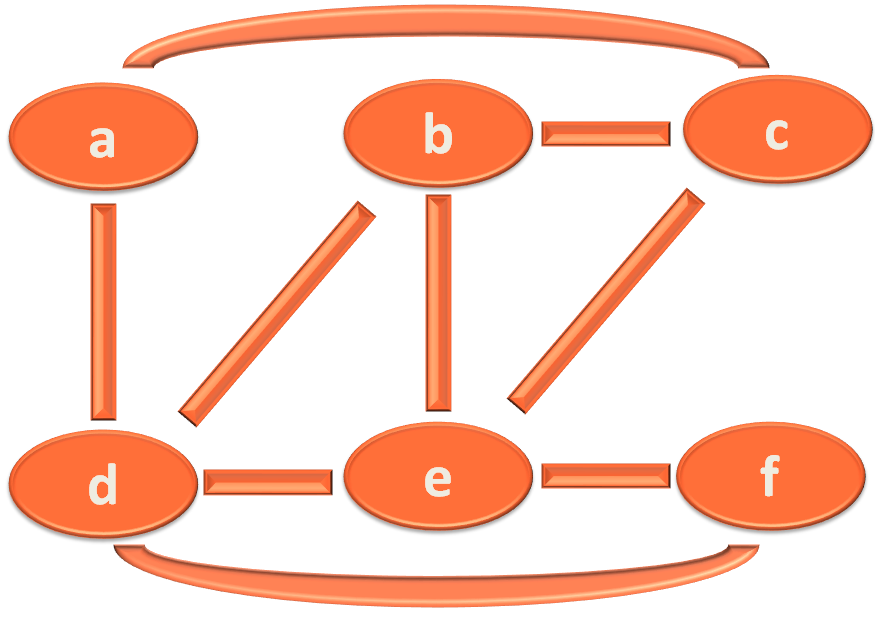
We can take various ways to navigate the graph using Depth First Search (DFS). Just remember our main intension is to visit all the vertices.

In this case we have covered the graph in the following path :

a --> c --> b --> d --> e --> f

Let us see how ?

Code Explanation for DFS - Depth First Search - Recursive :

Below code explains the methods :

fun constructAdjacencyList(vtx: String, adjcVertex: String)

fun insertVertex(vertex: String)

Almost the same we have discussed in DFS - Depth First Search - Iterative approach. You can skip it if you wane to.

Click Here - To understand the details of the methods 'fun constructAdjacencyList(vtx: String, adjcVertex: String)' and 'fun insertVertex(vertex: String)'.

Let's list out, what all do we need to support Depth First Search Data Structure.

We need a Linked List to store the vertices.

We need a doubly Linked List to store the adjacency linked list.

We need a Queue and an array to store its Levels.

We need a boolean array to store the Vertices that are already visited.

Now, let us see the above code.

We have a Linked List to store the Vertices.

var vertices = LinkedList<String>();

We also have a doubly Linked List to store the Adjacency List.

var adjacencyList = LinkedList<LinkedList<String>>();

And, there is a boolean array to store the Vertices that are visited.

var visited: BooleanArray = booleanArrayOf();

Note : The variables are marked as static, so that they could be accessed from main(...) method.

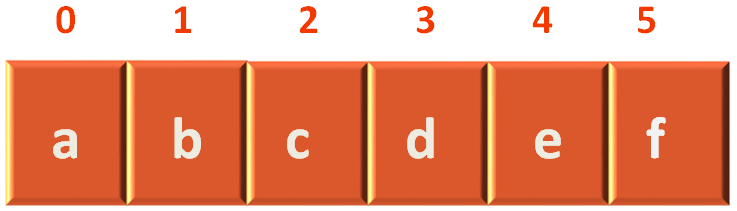
So, the first thing we will do is, insert the Vertices to the var vertices = LinkedList<String>(); Linked List.

vertices = LinkedList<>();

dfsRecursion.insertVertex("a");
dfsRecursion.insertVertex("b");
dfsRecursion.insertVertex("c");
dfsRecursion.insertVertex("d");
dfsRecursion.insertVertex("e");
dfsRecursion.insertVertex("f");

Explanation of 'fun insertVertex(vertex: String)' method

fun insertVertex(vertex: String) {

	vertices.add(vertex);
}

fun insertVertex(vertex: String) is quite simple.

There is just one statement in it.

vertices.add(vertex);

It accepts String vertex as a parameter and adds it to the Linked List, vertices.

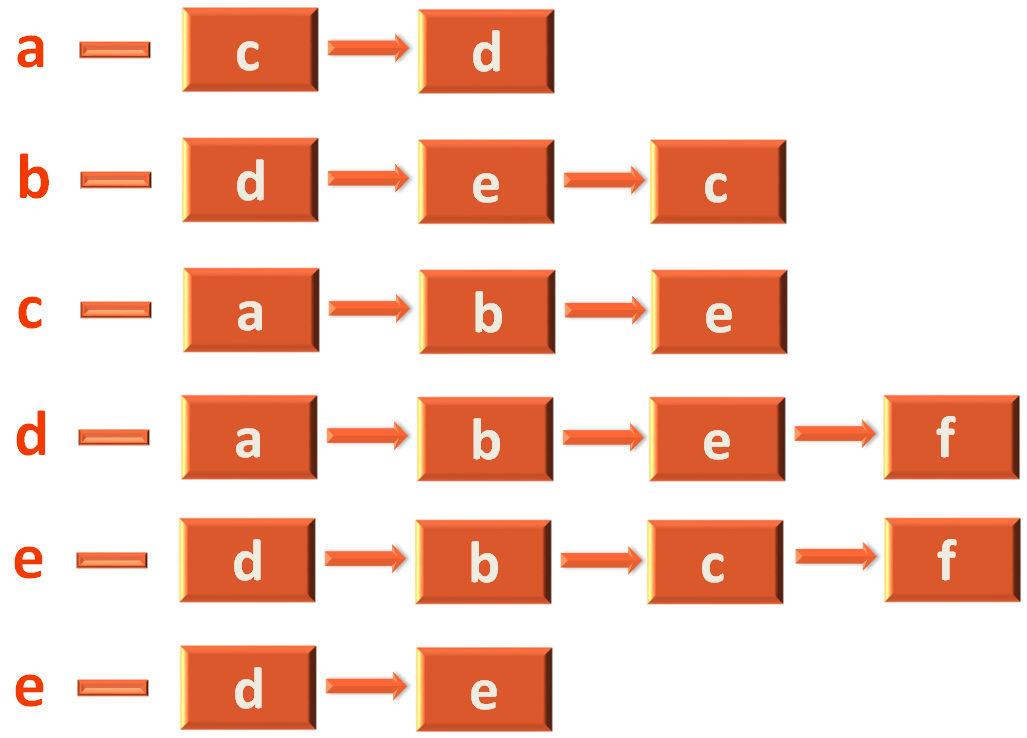
The next thing we will do is, create an Adjacency List to track the Adjacent Vertices.

Let us take the example of vertex a, to explain the creation of Adjacency List.

As we have seen, a has two adjacent vertices(i.e. c and d). And we have used the constructAdjacencyList(...) method to construct the Adjacency Matrix.

dfsRecursion.constructAdjacencyList("a", "c");
dfsRecursion.constructAdjacencyList("a", "d");

Note : Just remember, creating an Adjacency List above is same as creating an Edge. As the Adjacency List is actually a group of Edges.

Explanation of 'fun constructAdjacencyList(vtx: String, adjcVertex: String)' method

fun constructAdjacencyList(vtx: String, adjcVertex: String) {

	var vtxIndex = vertices.indexOf(vtx);

	adjacencyList.add(LinkedList<String>());
	adjacencyList.get(vtxIndex).add(adjcVertex);
}

Although, the above method is explained in Adjacency List Code tutorial. I will give a brief explanation in this tutorial.

When a method call is made,

The variable vtx is assigned with value "a" and adjcVertex is assigned with "b".

Now, the first line,

var vtxIndex = vertices.indexOf(vtx);

Calculates the index/position of Vertex a. And as we can see the index a is 0.

Now, in the next line,

adjacencyList.add(LinkedList<String>());

We are initialising the first row of the 2D Linked List, adjacencyList.

But with what ?

We are initialising it with a Linked List LinkedList<String>(),

adjacencyList.add(LinkedList<String>());

So that the first row can hold the Adjacency List for vertex a.

a   ---   c ---> d

Similarly, the second row should hold the Adjacency List for vertex b and so on.

And in this iteration, our target is to find out the first row(To create an Adjacency List for vertex a) and insert vertex b to it.

And the below code does that.

adjacencyList.get(vtxIndex).add(adjcVertex);

We get the index of vertex a

vtxIndex = vertices.indexOf(vtx);

As we know vtx is a.

Then add adjcVertex(That contains vertex c) to the 0th index of adjacencyList.

adjacencyList.get(0).add("c");

And following it we form the Adjacency List.

Now, we come across the most important method fun depthFirstSearch(source: String) that performs the Depth First Search (DFS).

Explanation of 'fun depthFirstSearch(source: String)' method

fun depthFirstSearch(source: String){

	var sourceIndex = vertices.indexOf(source);

	visited[sourceIndex] = true;

	print("$source   ");

	var iter = adjacencyList.get(sourceIndex).iterator();
	while (iter.hasNext() ) {

		var str = iter.next();

		var i = vertices.indexOf(str);

		if (visited[i] == false) {

			visited[i] = true;
			depthFirstSearch(str);
		}
	}
}

We have called the fun depthFirstSearch(source: String) from the main method passing a as the parameter.

dfsRecursion.depthFirstSearch("a");

So, the first thing we will do is, take the index of a,

var sourceIndex = vertices.indexOf(source);

Now, if we see the List of vertices,

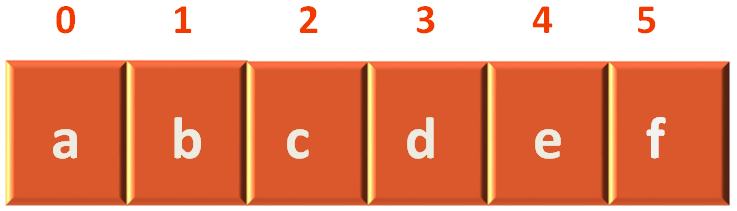
We can see that a lies in index 0.

Next, we mark a as visited,

visited[sourceIndex] = true;

in the visited[] array,

visited[0] = true;

Then we print the vertex a.

print("$source   ");

Output :

Then comes the while(...) loop, where we find the adjacent vertices of the top element(i.e. a).

var iter = adjacencyList.get(sourceIndex).iterator();
while (iter.hasNext() ) {

	var str = iter.next();

	var i = vertices.indexOf(str);

	if (visited[i] == false) {

		visited[i] = true;
		depthFirstSearch(str);
	}
}

And the for loop itself needs a little explanation.

The first statement of the for loop (i.e. The initialisation section of the loop),
```
var iter = adjacencyList.get(sourceIndex).iterator();
```
is where we get the Adjacent Vertices of vertex c in the var iter.

Thinking How ?

Well ! The adjacencyList is a 2D Linked List that stores the adjacent vertices. And the trick is played in,
```
adjacencyList.get(sourceIndex).iterator()
```
As we have seen, the sourceIndex is 0 (Because the index of vertex a is 0).

And the iter variable of Iterator gets the adjacency list of vertex a in it.

The next statement,
```
iter.hasNext()
```
tells the for loop to continue until there are elements in the list.

And ! Well ! There is no increment section. We have left it blank

iter variable of Iterator, stores the Adjacency List of vertex a in it.So, iter has the elements c and d in it.

Now, str contains the first adjacent vertex c.

str = iter.next();

Next, we find the index of vertex c,

var i = vertices.indexOf(str);

Now, if we see the List of vertices,

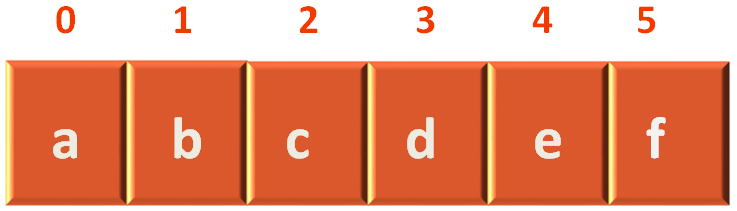
We can see that c lies in index 2.

So, we check if c is visited or not.

if (visited[i] == false) {

	visited[i] = true;
	depthFirstSearch(str);
}

Now, if we check the visited array,

We found that visited[2] = false and we get into the if statement.

And marked visited[2] = true,

visited[i] = true;

In the visited[] array,

And then comes the fun part. Where the depthFirstSearch(...) method calls itself.

depthFirstSearch(str);

So, internally what happens is, kotlin maintains an internal stack, that is hidden from you.

Now, since the method started from a, kotlin puts a to the stack. Then whenever it meets the statement,

depthFirstSearch(str);

It recognises a recursive call is made and pushes the content of variable str(i.e. c) to the stack.

Similarly, we repeat the same process until all the vertices are visited. And kotlin pushes all the values to the stack.

Now, since we have reached a place where all the adjacent vertices of vertex f are visited.

So, it's time for kotlin to backtrack. i.e. Start popping out all the elements from its internal queue.

So, it takes out f out of the queue and checks if there are any adjacent vertices of e that are not visited.

Continuing in the same way, all the elements are popped out of the Queue and the execution ends.

❮❮ PREV NEXT ❯❯