

Kruskal's Algorithm is one of the simplest algorithm that gives us an efficient solution for constructing a Minimum Spanning Tree.
And Kruskal's Algorithm uses the Greedy approach to construct a Minimum Spanning Tree.
What is Greedy approach ?
Just imagine, a person who is Greedy for food, will eat anything he gets. And the same logic applies here.
We will start picking whatever edge we get first.
Let us take the below Graph with lengths/weights.
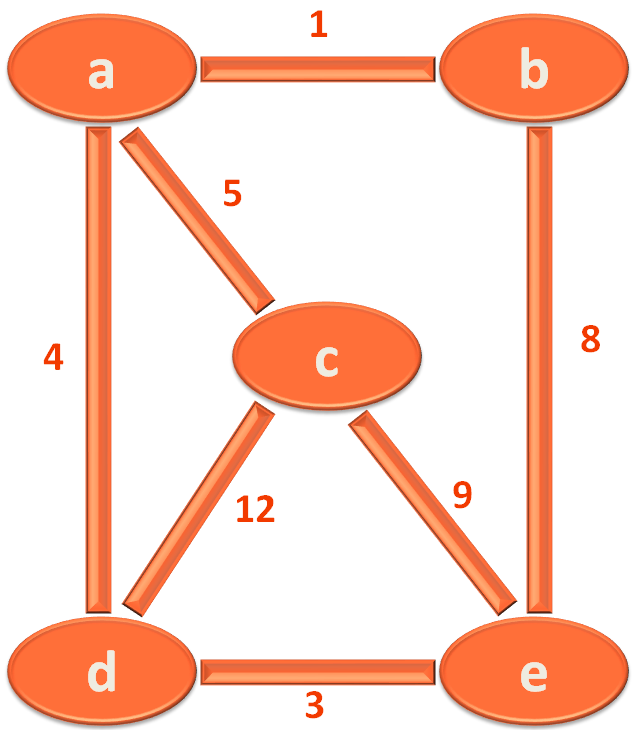
Let us see the edge and its corresponding length.

Now, according to Kruskal's algorithm.

At first, comes the edge a,b. With the length 1.

Then, we have the edge d,e. With a length 3.

Next, comes the edge a,d. With length 4.

Then, comes the edge a,c. With length 5.

Next, comes the edge b,e with length 8.
Now, if we place the edge b,e. It forms a cycle ( i.e. b,e,d,a,b).
And a spanning tree shouldn't be having cycles.
So, we do not include the edge b,e.
Now, we need to include the edge c,e with length 9. But it also forms a cycle ( i.e. a,c,e,d,a).
So, we cannot include the edge c,e as well.
And lastly, we come to the edge c,d with length 12.
But, including the edge c,d also forms a cycle in the graph( i.e. a,c,d,a).
And finally we have the Minimum Spanning Tree using Kruskal's Algorithm.

So, Kruskal's Algorithm is a three step process :
So far so good !
Now, the only concern is, how do you determine, if including an edge forms a cycle or not?
Let us understand it in detail.
Let us relook at the above example again.
We have the below Graph :

And we have listed the edges and its corresponding lengths :

The first thing we have done is, sorted the edges according to its length/weight.

Now, the fun begins here,
We will take all the 5 vertices and put them in individual groups.

Next, we will start taking the sorted edges and start placing them, one by one.
And the first edge is a,b with length 1.
So, the first thing we do is, check if the vertex 'a' and 'b' are in different groups.
And, we can see that vertex 'a' and 'b' are in different groups. So, let us put vertex 'a' and 'b' in one group.
And let's connect 'a' and 'b'.
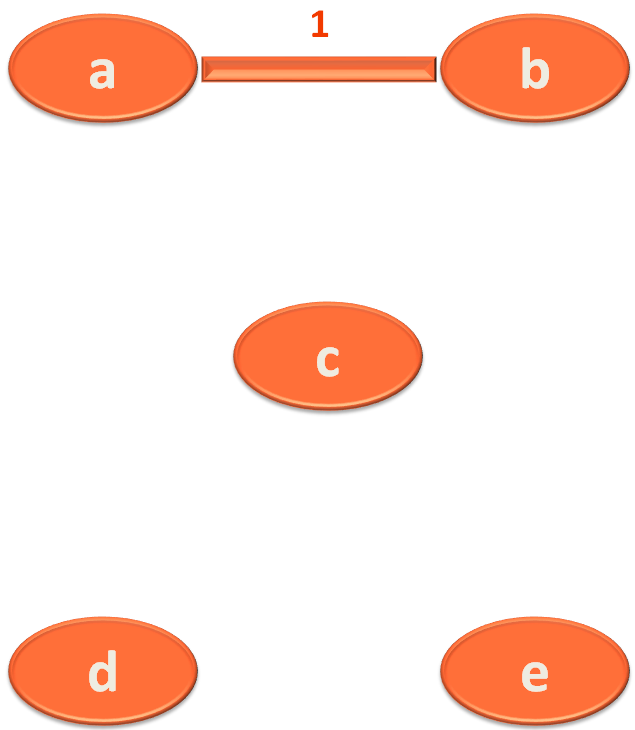
And the next edge is d,e with length 3.
Similarly, we check if the vertex 'd' and 'e' are in different groups.
And, we can see that vertex 'd' and 'e' are in different groups. So, let us put vertex 'd' and 'e' in one group.
So, let's connect vertex 'd' and 'e'.

Then, we come to the next edge a,d of length 4.
And, even in this case, we can see that vertex 'a' and 'd' are in different groups.
So, we combine the group of 'a' with the group of 'd'.
And we get,
So, we connect vertex 'a' and 'd'.

Next, comes the edge a,c with length 5.
So, we check if the vertex 'a' and 'c' are in different groups or not.
And found, they are in different groups. So, we place them in the same group.
And, connect 'a' and 'c'.
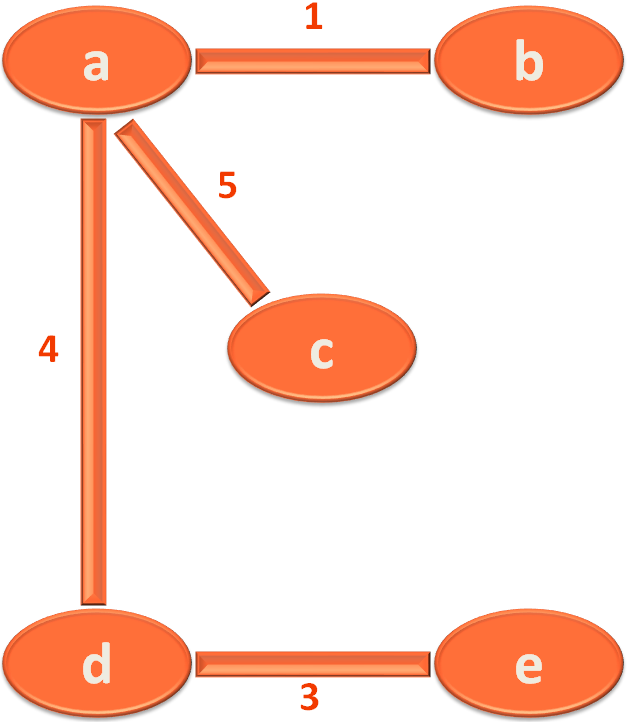
Next, comes the edge b,e with length 8.
So, we check if vertices 'b' and 'e' are in the same group or not.
And found that they are in the same group. So, we do not include the edge b,e.
Now, if you look at the graph.
If we place the edge b,e. It forms a cycle (i.e. b,e,d,a,b).
And a spanning tree shouldn't be having cycles.
So, we do not include the edge b,e.
Similarly, we check if the next edge c,e with length 9, is in the same group or not.
And they are in the same group and it forms a cycle (i.e. a,c,e,d,a).
So, we do not include them as well.
And lastly, we come to the edge c,d with length 12. But they are also in the same group and including the edge c,d also forms a cycle in the graph(i.e. a,c,d,a).
So, we don't include this edge as well.
And the minimum spanning tree using Kruskal's Algorithm is,

Running time of Kruskal's Algorithm : O(n log n)