PRIM's ALGORITHM - MINIMUM SPANNING TREE - IMPLEMENTATION

Actual implementation of Prim's Algorithm for Minimum Spanning Trees

Let us recall the steps involved in Prim's Algorithm :

First step is, we select any vertex and start from it(We have selected the vertex 'a' in this case).
Then, we try finding the adjacent Edges of that Vertex(In this case, we try finding the adjacent edges of vertex 'a').

This is the time for you to pause !

And think, what have we used to find the Adjacent Edges in the previous tutorials.

And yes ! It was Adjacency List.

If you had already forgotten it, it is recommend to go and check out the 'Adjacency List' tutorial. If you don't want, no worries! We will explain 'Adjacency List' in brief.

Just remember that we will be using 'Adjacency List' for finding the Adjacent Edges.
Next, we will take all the Adjacent edges from above and check, which edge has the smallest length/weight.

Again, it's time for you to pause and think! Which data structure is best suited for finding a minimum element.

And it's none other than a Min-Heap that helps us find the Min element in O(1) time.

Again, it is recommended to revisit 'Heap' tutorial to understand Min-Heap. If you don't want to, no worries. We will explain it in brief.

So, the moral of the story is, we will be using Adjacency List to store the Adjacent Edges and Min-Heap data structure to find the Edge of minimum length.

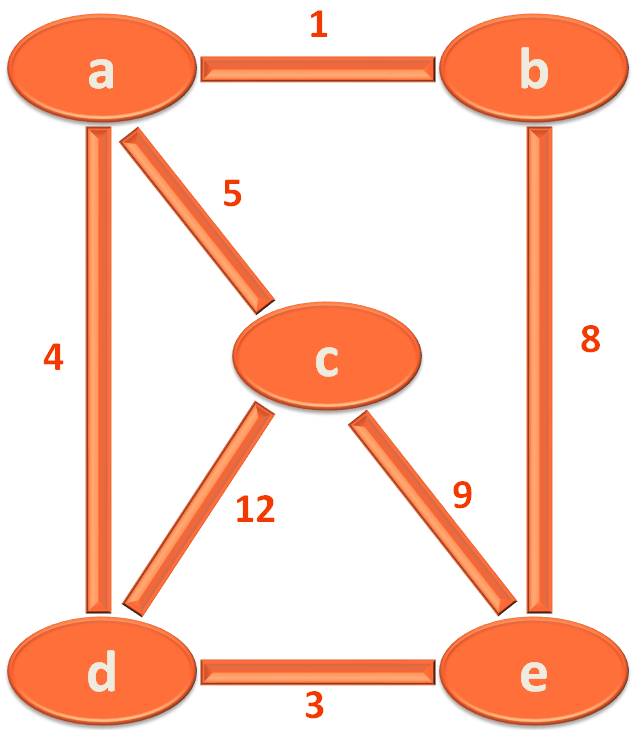
Now, let us take the Graph, we are using so far and see how to find the Minimum Spanning Tree by Prim's Algorithm using the Adjacency List and Min-Heap data structure.

As said above, we need to put the edges in the Min-Heap. As we need to find the Edge with minimum length, in each iteration.

Now, just pause ! Think for moment!

An Edge has a 'startVertex', 'endVertex' and the 'value'. So, are we suppose to store all of them in the Heap.

No, we won't !

Rather, we would be following a different process.

Now, let us take the same example, of you being a courier delivery guy, to understand this.

Example :

Let us consider that the vertices a, b, c, d and e are cities. And you are the courier delivery boy.

Now, your boss has assigned you a task, to find out the minimum distance between the cities.So, that it can save the travelling distance for other courier guys.

Now, you are intelligent enough to figure out that you need a Min-Heap data structure to store the Edge Length(And not the entire edge).

And, how would you do that?

Say when you have travelled from City/Vertex 'a' to City/Vertex 'b'. You would simply mark the City/Vertex 'b' with the length of (a,b), i.e. 1.

Similarly, when you have travelled from City/Vertex 'd' to City/Vertex 'e'. You would simply mark the City/Vertex 'e' with the length of (d,e), i.e. 3.

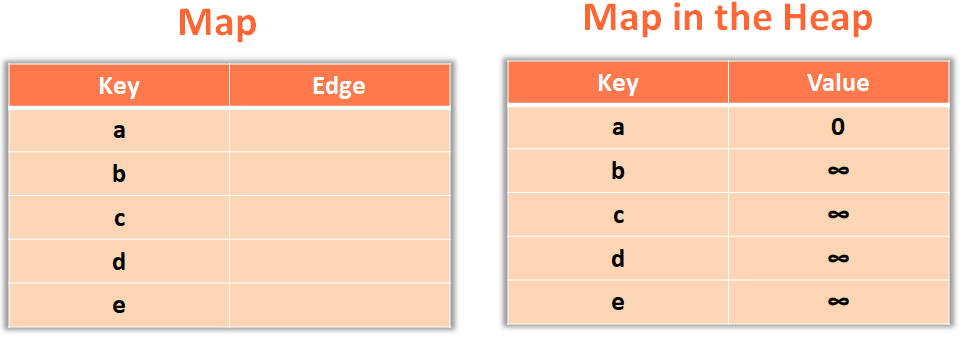
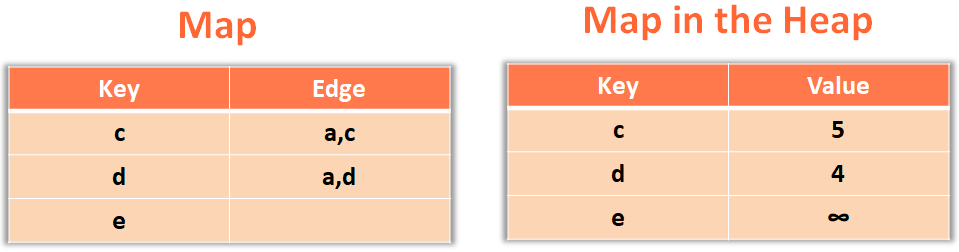
And, you would be maintaining a Map data structure to put the Map into the Heap. Where the key will be the Vertex name and the value will be the length.

In the above case, vertex 'e' would be the key and '3' would be the value.

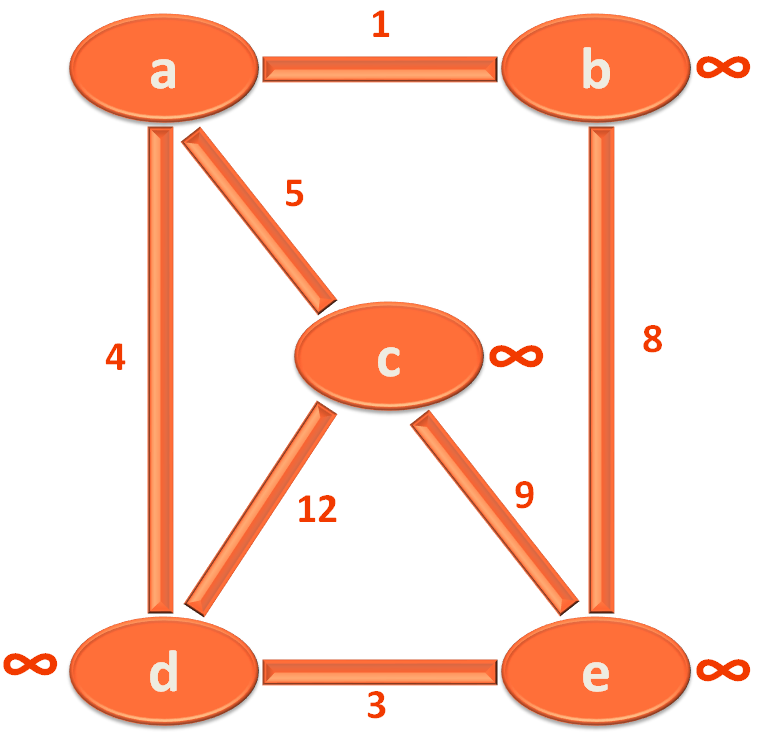
And initially we will mark all the Vertices with '∞'. Except the starting vertex, that will be marked with '0'.

But why '∞'?

Because we are suppose to find the smallest edge length from Heap. And '∞' can be considered as a very large value, that is not yet assigned. We will understand this eventually.

Let us suppose, you have started from Vertex/City 'a'. So, you would be marking 'a' with '0' and rest of the Vertices/Cities with '∞'.

The next thing we will do is, create a Map with the vertex/city name as key and the edge length as the value.

And place the above Map in the Heap.

Note :You can go through the Heap tutorial to understand how a Heap works. If not, don't worry, just remember, we are using Heap because it's time efficient. Just recall, we are suppose to find the minimum edge length. So, we put all the key and values of the above Map to the Heap. And Heap helps us find the Minimum element in O(1) time and then rearranging the Heap takes O(log n) time.

Now, just think ! We have already placed the Map with key as Vertex and its value as the Edge length. But how will you determine, which Edge has that particular length?

And yes ! We need one more Map, that will have the same Vertex and the key and the actual Edge (With start and end vertex) as its value.

So, initially all the edges will be blank in the Map and we will start from the starting Vertex/City 'a'.

Since 'a' is the starting vertex with value '0'. We can take it out of the Map in the Heap and from the Map as well.

Now, let us look at the Graph we have.

Now, according to Prim's Algorithm, the first thing you will do is,

Choose a starting Vertex/City. You can choose any Vertex/City.

And, you have chosen the Vertex/City 'a'.
Then you will have to check, which all Vertices/Cities are reachable from Vertex/City 'a'.

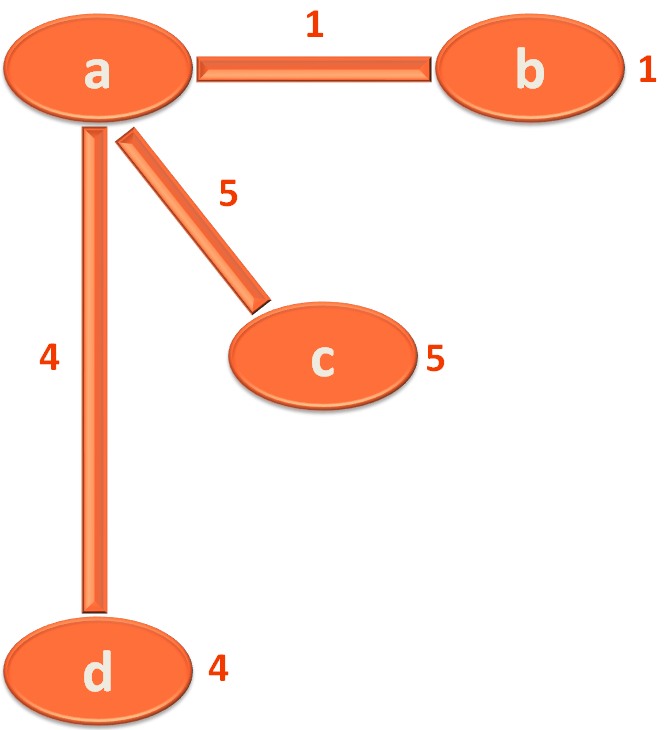
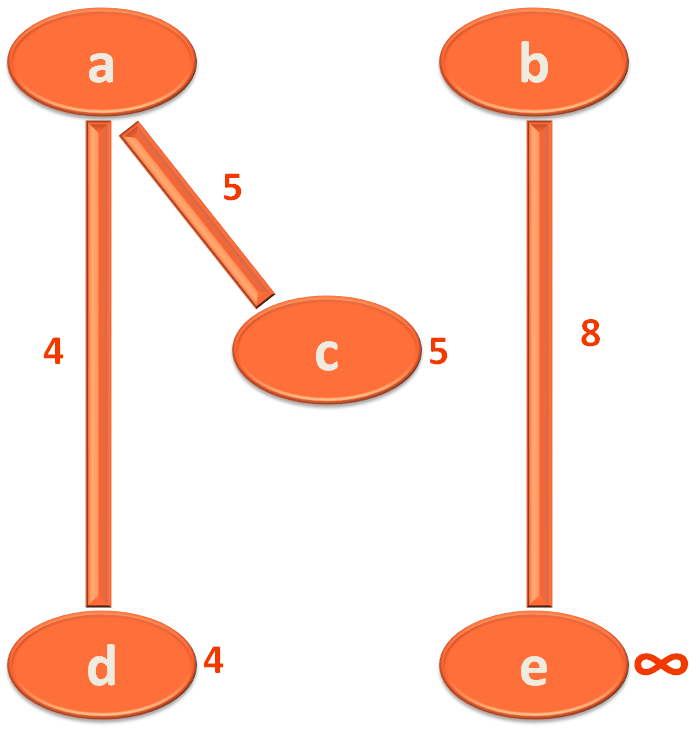
And you find that there are three Vertices/Cities that could be reachable from Vertex/City 'a'. They are 'b', 'c' and 'd'.

So, you mark 'b' with 1, 'c' with 5 and 'd' with 4.

Also make the same change in the Map and Map in Heap.

Now, you have to check, whichever among the three Edge/Road(i.e. 'a,b', 'a,c' and 'a,d') has the smallest Edge Length/Distance.

So, we will go to the 'Map in the Heap' and run a 'MinHeap' operation. In simple words, we will try finding the smallest value in the 'Map in the Heap'.

In this case, vertex 'b' in 'Map in the Heap' has the lowest value i.e. 1.

The next thing we have to do is, find out, which Edge is associated with Vertex 'b'.So, we go to the 'Map' and check the Edge associated with vertex 'b'.

And find that the Edge a,b is associated with the vertex 'b'.

So, we take 'a,b' as the first edge/road for your Minimum Spanning Tree.

And delete the record 'b' from 'Map in the Heap' and from the Map as well.
Now since, you have the first edge/road for your Minimum Spanning Tree.

Next, you have to check, which all Vertices/Cities are reachable from Vertex/City 'a' and 'b'.

But, we will exclude the edge/road a,b, as that are already included in the Minimum Spanning Tree.

And, in this case Vertex/City 'd' and 'c' is reachable from Vertex/City 'a'.

And, Vertex/City 'e' is reachable from Vertex/City 'b'.

The next thing we will do is, replace the value of vertex/city 'e' with 8 in the 'Map in the Heap'. Also, we will go to the 'Map' and replace the value of vertex/city 'e' with the Edge b,e.

Now, as usual you have to check, whichever among the three Edge/Road(i.e. 'a,d', 'a,c' and 'b,e') has the smallest Edge Length/Distance.

So, we will go to the 'Map in the Heap' and run a 'MinHeap' operation. In simple words, we will try finding the smallest value in the 'Map in the Heap'.

In this case, vertex 'd' in 'Map in the Heap' has the lowest value i.e. 4.

Then we will check, which Edge is associated with Vertex 'd'.

So, we go to the 'Map' and check the Edge associated with vertex 'd'.

And find that the Edge a,d is associated with the vertex 'b'.

And also delete, the vertex/city 'd' from both 'Map in the Heap' and the 'Map'.

So, you take 'a,d' as the second edge/road for your Minimum Spanning Tree.
Now, you have two edges for your Minimum Spanning Tree.

Next, as usual you have to check, which all vertices are reachable from Vertex/City 'a','b' and 'd'.

Just remember, you have to exclude the edges/roads that are already included in the Minimum Spanning Tree.

And, in this case Vertex/City 'c' is reachable from Vertex/City 'a'.

Similarly, Vertex/City 'e' is reachable from Vertex/City 'b'.

And, Vertex/City 'e' and 'c' is reachable from Vertex/City 'd'.

Now, if we go to 'Map in the Heap', we can see the current value of Vertex/City 'e' is 8. But right now we have a new value 3 that is of the edge (d,e).

And the most important thing is, 3 is less than 8.

So, we replace the value of Vertex/City 'd' with 3 and also go to the Map and replace the value of Vertex/City 'd' with the new Edge (d,e)

Now, we will go to the 'Map in the Heap' and run a 'MinHeap' operation. In simple words, we will try finding the smallest value in the 'Map in the Heap'.

In this case, vertex 'e' in 'Map in the Heap' has the lowest value i.e. 3.

Then we will check, which Edge is associated with Vertex 'e'.

So, we go to the 'Map' and check the Edge associated with vertex'd'.

In this case, the edge 'd,e' is associated with Vertex/City 'e'.

And also delete, the vertex/city 'e' from both 'Map in the Heap' and the 'Map'.

So, you take 'd,e' as the third edge/road for your Minimum Spanning Tree.
Now, you have three edges/roads for your Minimum Spanning Tree.

Next, as usual you have to check, which all vertices are reachable from Vertex/City 'a', 'b', 'd' and 'e'.

Do not forget, you have to exclude the edges/roads that are already included in the Minimum Spanning Tree.

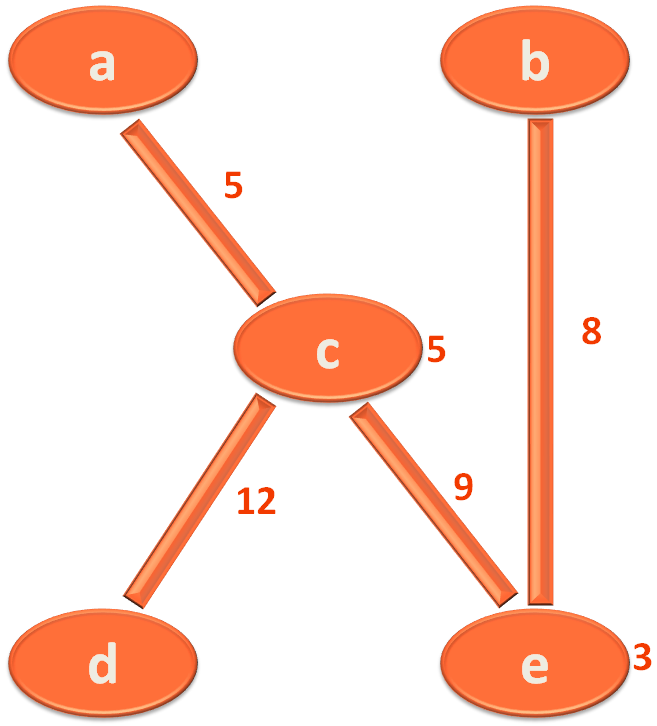
And, in this case Vertex/City 'c' is reachable from Vertex/City 'a'.

Similarly, Vertex/City 'c' is also reachable from Vertex/City 'd'.

Vertex/City 'c' is also reachable from Vertex/City 'e'.

And, Vertex/City 'e' is reachable from Vertex/City 'b'.

Now, if we go to 'Map in the Heap', we can see the current value of Vertex/City 'c' is 5. But right now we have a new value 12 that is of the edge (d,c).

And 12 is greater than 5. So, we do not replace the edge with the new value in the 'Map in the Heap'.

Also, we have one more value i.e. 9, which is of the edge (e,c).

But 9 is also greater than 5. So, we do not include that as well.

And finally we are left with the edge (a,c) with value 5.

So, you take 'a,c' as the last and final edge/road for your Minimum Spanning Tree.

And delete the entry for Vertex/City 'c' from the 'Map in the Heap' and 'Map'.

Now, since there are no more entries in the Minimum Spanning Tree, we should stop here.

So, you just got your Minimum Spanning Tree using Prim's Algorithm. And Congrats, your boss is happy and you got Promoted.

❮❮ PREV NEXT ❯❯