Learnerslesson
   JAVA   
  SPRING  
  SPRINGBOOT  
 HIBERNATE 
  HADOOP  
   HIVE   
   ALGORITHMS   
   PYTHON   
   GO   
   KOTLIN   
   C#   
   RUBY   
   C++   
   HTML   
   CSS   
   JAVA SCRIPT   
   JQUERY   
JAVA SPRING SPRINGBOOT HIBERNATE HADOOP HIVE ALGORITHMS PYTHON GO KOTLIN C# RUBY C++ HTML CSS JAVA SCRIPT JQUERY


❮❮ PREV NEXT ❯❯


PRIM's ALGORITHM - MINIMUM SPANNING TREE


Let us take the old example that you are a Courier delivery guy. You deliver packages to various Cities.


Example :


Now, your Boss is very pleased with your work and offered you a promotion, only if you can find out the shortest distance between the Cities.


Now, you are intelligent enough to guess that he is talking about a Minimum Spanning Tree.


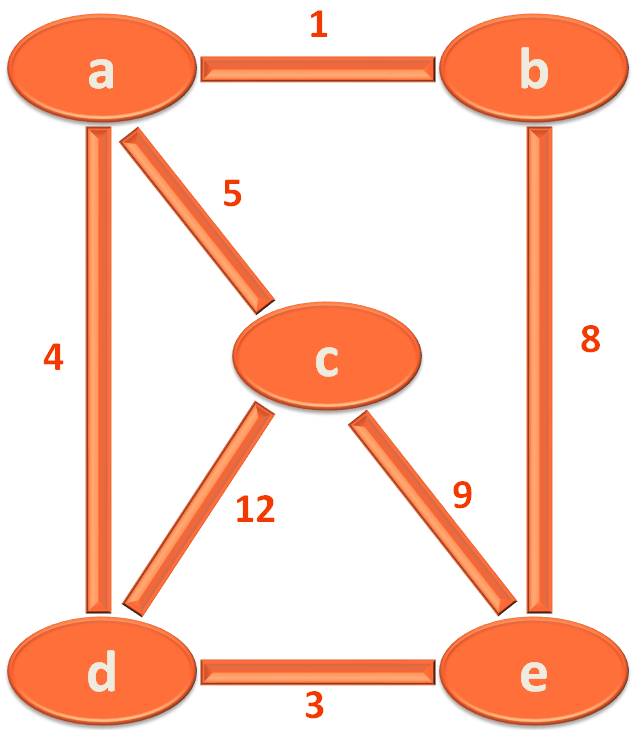
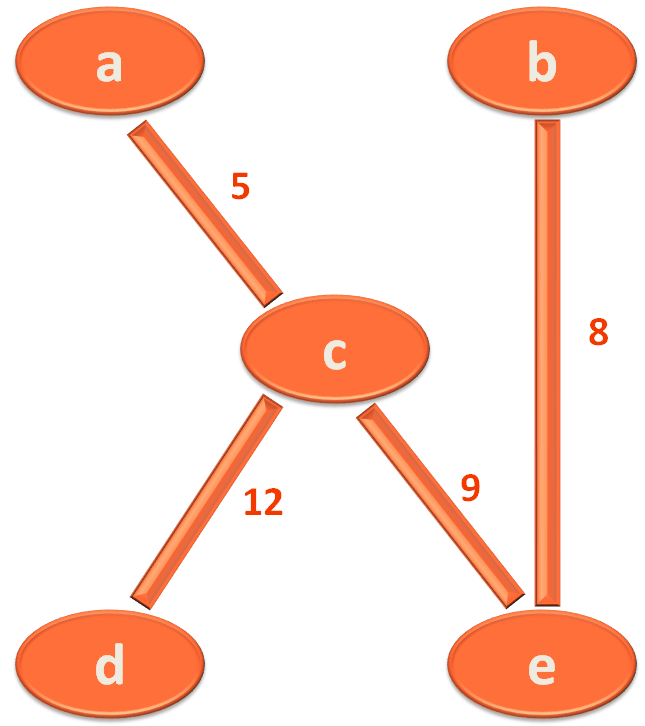
java_Collections

a, b, c, d and e are the cities and the edges are the roads that connects the Cities. Also, the edges/roads have, say distance/lengths mentioned.


Like city/vertex a and b are connected by a road/edge and the distance between them is 1.


Let us list out all the edge/roads and its corresponding length/distance between the cities.


java_Collections

This time to construct the Minimum Spanning Tree, you would be using Prim's Algorithm.


And Prim's Algorithm also uses the Greedy approach to construct a Minimum Spanning Tree.


What is Greedy approach ?


Just imagine, a person who is Greedy for food, will eat anything he gets. And the same logic applies here.


We will start picking whichever edge we get first.


Now, according to Prim's Algorithm, the first thing you will do is,


  1. Choose a starting Vertex/City. You can choose any Vertex/City.

    Let's say, you have chosen the Vertex/City 'a'.
  2. Then you will have to check, which all Vertices/Cities are reachable from Vertex/City 'a'.

    And you find that there are three Vertices/Cities that could be reachable from Vertex/City 'a'. They are 'b', 'c' and 'd'.

    java_Collections


    Now, you have to check, whichever among the three Edge/Road(i.e. 'a,b', 'a,c' and 'a,d') has the smallest Edge Length/Distance.

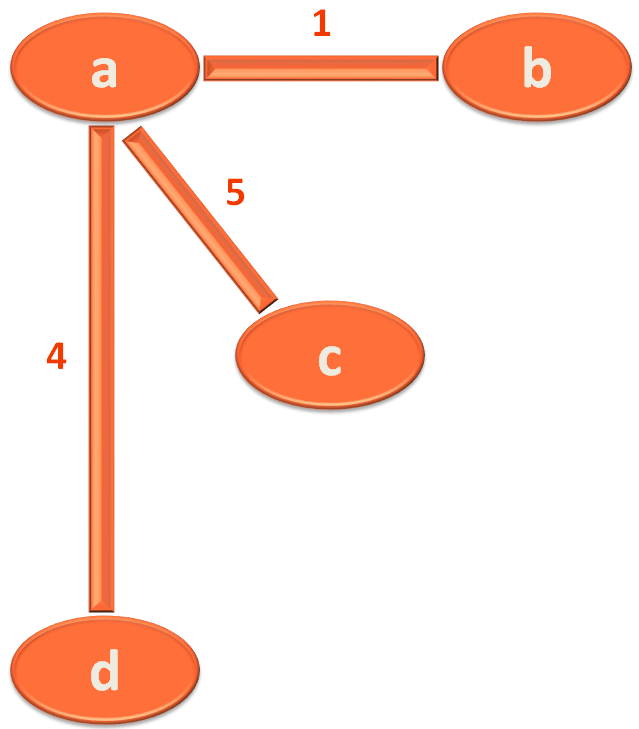
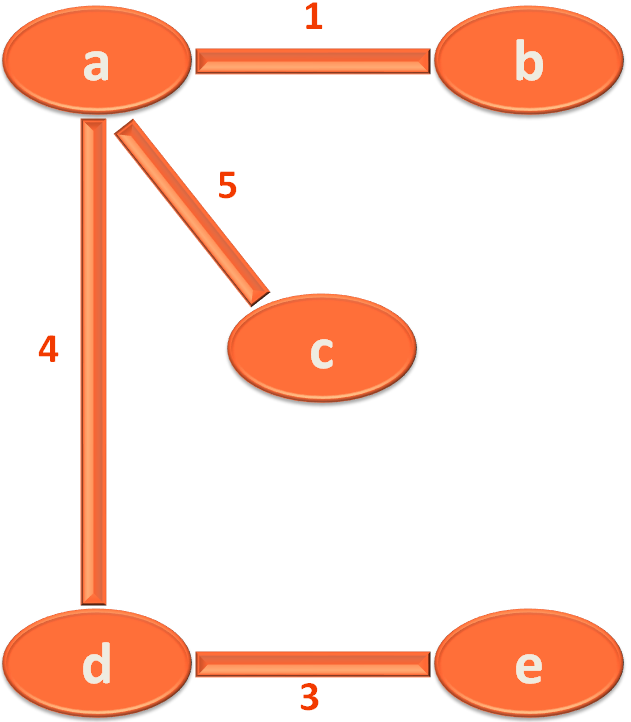
    In this case, the edge 'a,b' has the smallest Length/Distance 1.

    So, you take 'a,b' as the first edge/road for your Minimum Spanning Tree.

    java_Collections
  3. Now since, you have the first edge/road for your Minimum Spanning Tree.

    Next, you have to check, what all vertices are reachable from Vertex/City 'a' and 'b'.

    But, we will exclude the edge/road a,b, as that are already included in the Minimum Spanning Tree.

    And, in this case Vertex/City 'd' and 'c' is reachable from Vertex/City 'a'.

    java_Collections


    Now, as usual you have to check, whichever among the three Edge/Road(i.e. 'a,d', 'a,c' and 'b,e') has the smallest Edge Length/Distance.

    In this case, the edge 'a,d' has the smallest Length/Distance 4.

    So, you take 'a,d' as the second edge/road for your Minimum Spanning Tree.

    java_Collections
  4. Now, you have two edges for your Minimum Spanning Tree.

    Next, as usual you have to check, which all vertices are reachable from Vertex/City 'a','b' and 'd'.

    Just remember, you have to exclude the edges/roads that are already included in the Minimum Spanning Tree.

    And, in this case Vertex/City 'd' and 'c' is reachable from Vertex/City 'a'.

    Similarly, Vertex/City 'e' is reachable from Vertex/City 'b'.

    And, Vertex/City 'e' and 'c' is reachable from Vertex/City 'd'.

    java_Collections


    Now, as usual you have to check, whichever among the four Edge/Road(i.e. 'a,c', 'd,c' 'd,e' and 'b,e') has the smallest Edge Length/Distance.

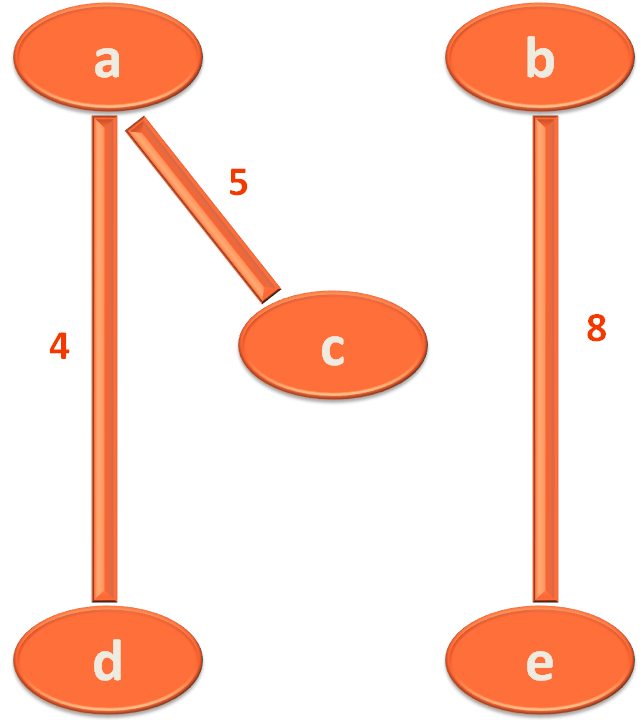
    In this case, the edge 'd,e' has the smallest Length/Distance 3.

    So, you take 'd,e' as the third edge/road for your Minimum Spanning Tree.

    java_Collections
  5. Now, you have three edges/roads for your Minimum Spanning Tree.

    Next, as usual you have to check, which all vertices are reachable from Vertex/City 'a','b', 'd' and 'e'.

    Do not forget, you have to exclude the edges/roads that are already included in the Minimum Spanning Tree.

    And, in this case Vertex/City 'c' is reachable from Vertex/City 'a'.

    Similarly, Vertex/City 'c' is also reachable from Vertex/City 'd'.

    Vertex/City 'c' is also reachable from Vertex/City 'e'.

    And, Vertex/City 'e' is reachable from Vertex/City 'b'.

    java_Collections


    Now, as usual you have to check, whichever among the four Edge/Road(i.e 'a,c', 'd,c' e,c and 'b,e') has the smallest Edge Length/Distance.

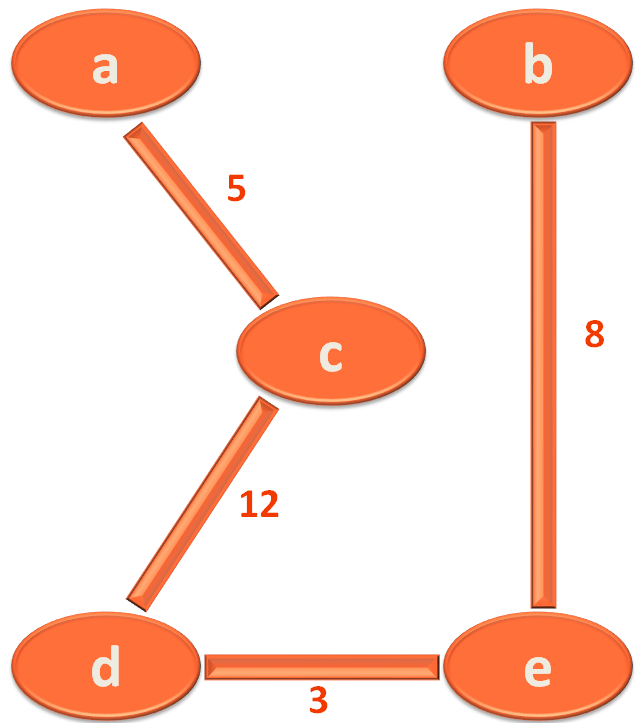
    In this case, the edge 'a,c' has the smallest Length/Distance 5.

    So, you take 'd,e' as the third edge/road for your Minimum Spanning Tree.

    java_Collections


    And adding any more edges/roads to the spanning tree would form a cycle. So, you just got your Minimum Spanning Tree using Prim's Algorithm. And Congrats, your boss is happy and you got Promoted.

    So, far so good. But how do you implement it?

    What I meant was, in order to write an efficient algorithm, we need a good data structure in terms of space and time complexity.

    And that is what we will see in the next tutorial.


❮❮ PREV NEXT ❯❯