GO - BFS - BREADTH FIRST SEARCH CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

package main
import "fmt"
import "sort"


var vertices []string
var adjacencyList [][]string
var visited []bool
var level []int

func insertVertex(vertex string) {

    vertices = append(vertices, vertex)
}

func constructTempList(tmpList *[]string, val string) {

	*tmpList = append(*tmpList, val)
}

func constructAdjacencyList(adjcList *[][]string, tmpList *[]string) {

    *adjcList = append(*adjcList, *tmpList)
    *tmpList = nil
}

func breadthFirstSearch(source string) {

    var queue []int

    sourceIndex := sort.StringSlice(vertices).Search(source)

    visited[sourceIndex] = true
    queue = append(queue, sourceIndex)

    for len(queue) != 0 {

        sourceIndex = queue[0]
            
        // Slice off the element once it is dequeued.
        queue = queue[1:]

		for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
                
            str := adjacencyList[sourceIndex][j]
                
            i := sort.StringSlice(vertices).Search(str);

            if (visited[i] == false) {

                visited[i] = true
                level[i] = level[sourceIndex] + 1
					
				queue = append(queue, i)
            }
        }
        fmt.Print(" --> ",vertices[sourceIndex]," of level ",level[sourceIndex])
    }
	fmt.Println()
}
	
func main() {
    
    const V = 5
    
    var tempList[]string
    
    visited = make([]bool, V)
    
    level = make([]int, V)

    // Adding vertices one by one

    insertVertex("a")
    insertVertex("b")
    insertVertex("c")
    insertVertex("d")
    insertVertex("e")

    // Create Adjacency List

	constructTempList(&tempList, "b")
    constructTempList(&tempList, "c")
    constructTempList(&tempList, "d")
    
    constructAdjacencyList(&adjacencyList, &tempList)
        
    constructTempList(&tempList, "a")
    constructTempList(&tempList, "e")
    
    constructAdjacencyList(&adjacencyList, &tempList)
        
    constructTempList(&tempList, "a")
    constructTempList(&tempList, "d")
    constructTempList(&tempList, "e")
    
    constructAdjacencyList(&adjacencyList, &tempList)
        
    constructTempList(&tempList, "a")
    constructTempList(&tempList, "c")
    constructTempList(&tempList, "e")
    
    constructAdjacencyList(&adjacencyList, &tempList)
        
    constructTempList(&tempList, "b")
    constructTempList(&tempList, "c")
    constructTempList(&tempList, "d")
    
    constructAdjacencyList(&adjacencyList, &tempList)
    
    breadthFirstSearch("c")
    
}

Output :

--> c of level 0 --> a of level 1 --> d of level 1 --> e of level 1 --> b of level 2

Code Explanation for BFS - Breadth First Search

Let's list out, what all do we need to support Breadth First Search Data Structure.

We need an Array to store the vertices.

We need a 2D Array to store the adjacency linked list.

We need an Array that would act like a Queue and an array to store its Levels.

We need a boolean array to store the Vertices that are already visited.

Now, let us see the above code.

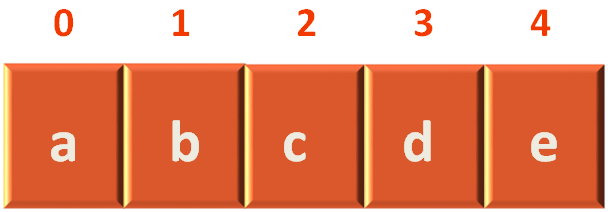
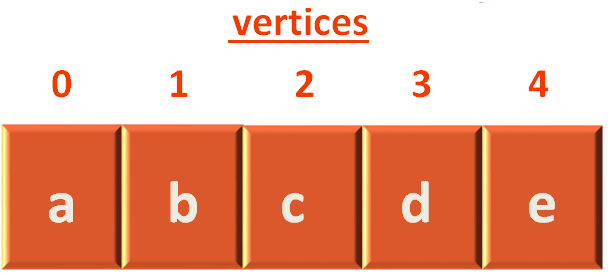
We have an Array to store the Vertices.

var vertices []string

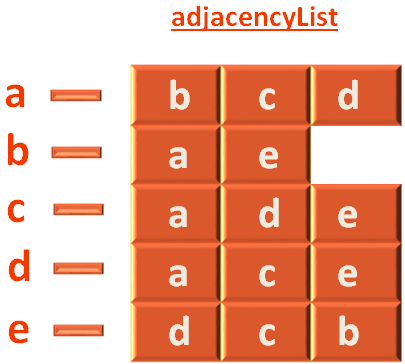
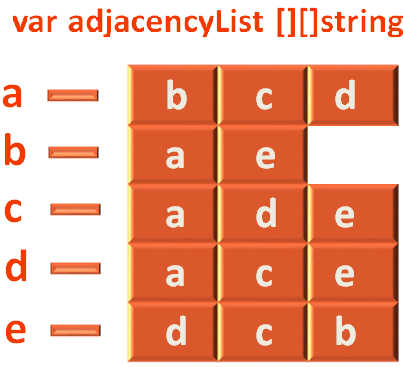
We also have a a 2D Array to store the Adjacency List.

var adjacencyList [][]string

Similarly, we have an Array that behaves like a Queue defined inside the method breadthFirstSearch(...).

var queue []int

And, we have an array to store the Levels.

var level []int

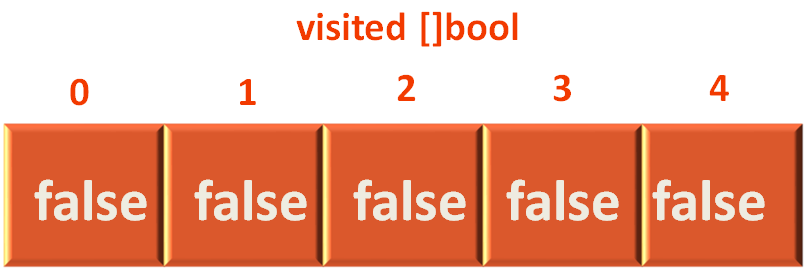
And, there is a boolean array to store the Vertices that are visited.

var visited []bool

So, the first thing we will do is, insert the Vertices to the var vertices []string Linked List.

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")

Explanation of 'func insertVertex(vertex string)' method

func insertVertex(vertex string) {

	vertices = append(vertices, vertex)
}

func insertVertex(vertex string) is quite simple.

There is just one statement in it.

vertices = append(vertices, vertex)

It accepts vertex string as a parameter and adds it to the Array, vertices[].

The next thing we will do is, create an Array to track the Adjacent Vertices.

Let us take the example of vertex a, to explain the creation of the Array to track the Adjacent Vertices.

As we have seen, a has three adjacent vertices(i.e. b, c and d). And we have used the func constructTempList(tmpList *[]string, val string) method to construct a tmpList[] Array. That would just hold the adjacent vertices of one node temporarily.

constructTempList(&tempList, "b")
constructTempList(&tempList, "c")
constructTempList(&tempList, "d")

And add them to the node.

constructAdjacencyList(&adjacencyList, &tempList)

Explanation of 'func constructAdjacencyList(adjcList [][]string, tmpList []string)' method

func constructAdjacencyList(adjcList *[][]string, tmpList *[]string) {

	*adjcList = append(*adjcList, *tmpList)
	*tmpList = nil
}

Although, the above method is explained in Adjacency List Code tutorial. I will give a brief explanation in this tutorial.

Initially, we create a tmpList[] Array. That would just hold the adjacent vertices of one node temporarily.

constructTempList(&tempList, "b")
constructTempList(&tempList, "c")
constructTempList(&tempList, "d")

Then we take the tempList[] Array and pass it to the func constructAdjacencyList(...).

constructAdjacencyList(&adjacencyList, &tempList)

The variable vtx is assigned with value "a" and adjcVertex is assigned with "b".

And in the first line itself,

*adjcList = append(*adjcList, *tmpList)

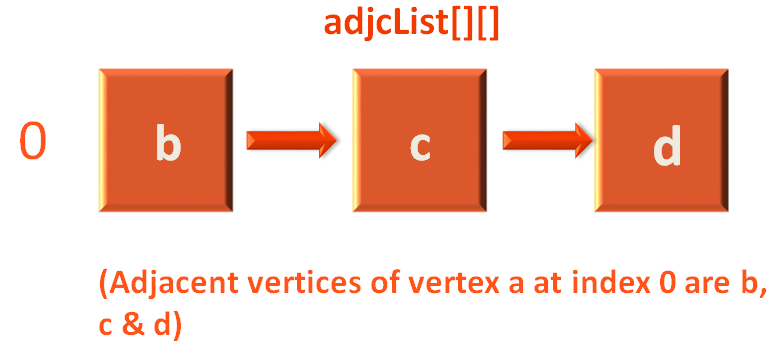
We are adding the contents of tempList[] array to the first row of adjcList[][] array.

So that the first row can hold the Adjacency List for vertex a.

a   ---   b ---> c ---> d

Continuing this way, we fill the 2d Array adjList[][] that stores the adjacency list.

Then we come across the most important method func breadthFirstSearch(source string) that performs the Breadth First Search (BFS).

Explanation of 'func breadthFirstSearch(source string)' method

func breadthFirstSearch(source string) {

	var queue []int

	sourceIndex := sort.StringSlice(vertices).Search(source)

	visited[sourceIndex] = true
	queue = append(queue, sourceIndex)

	for len(queue) != 0 {

		sourceIndex = queue[0]

		// Slice off the element once it is dequeued.
		queue = queue[1:]

		for j := 0; j < len(adjacencyList[sourceIndex]); j++ {

			str := adjacencyList[sourceIndex][j]

			i := sort.StringSlice(vertices).Search(str);

			if (visited[i] == false) {

				visited[i] = true
				level[i] = level[sourceIndex] + 1

				queue = append(queue, i)
			}
		}
		fmt.Print(" --> ",vertices[sourceIndex]," of level ",level[sourceIndex])
	}
	fmt.Println()
}

So, we are calling the method

breadthFirstSearch("c")

Passing the vertex c as source.

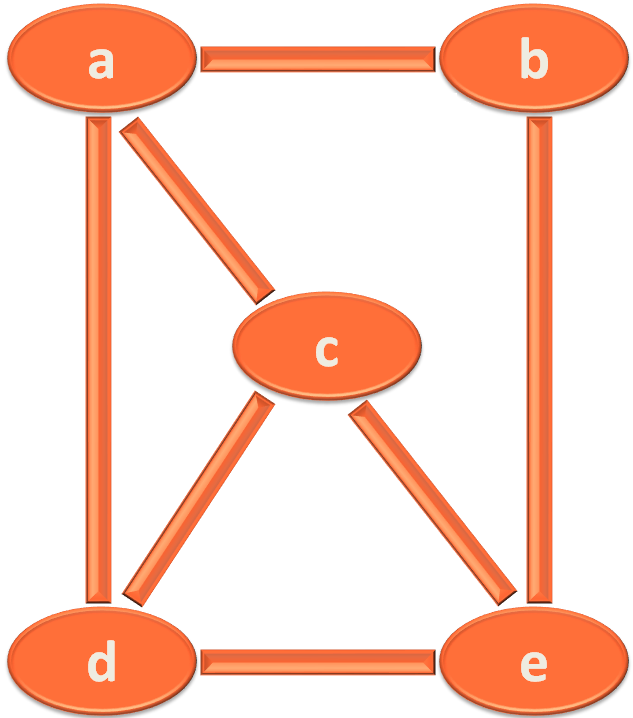
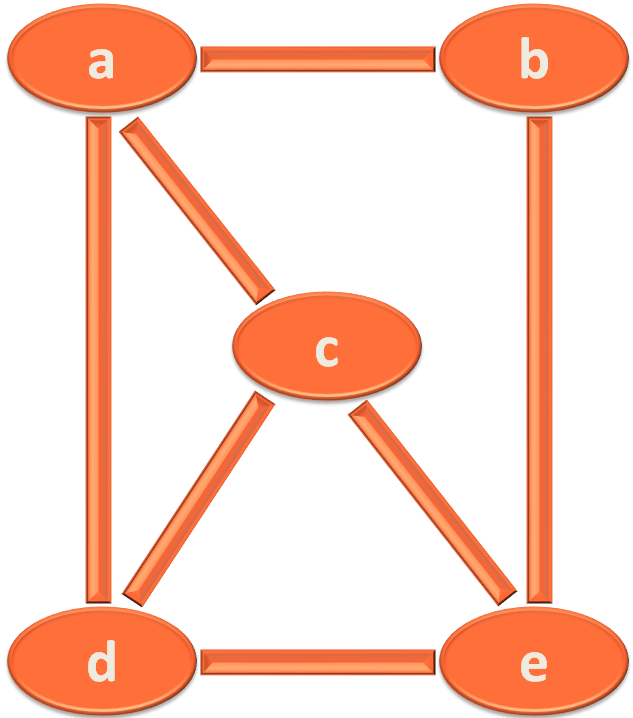
Below is the graph on which we had to perform a Breadth First Search (BFS).

To perform Breadth First Search (BFS), all we need is a Linked List to keep track of Vertices. Which we have in place.

And, we need a 2D Array to keep a track of Adjacent Vertices. And we also have that in place.

We also need a boolean array to keep a track of which all vertices are visited. Which we also have in place. All the values default to false.

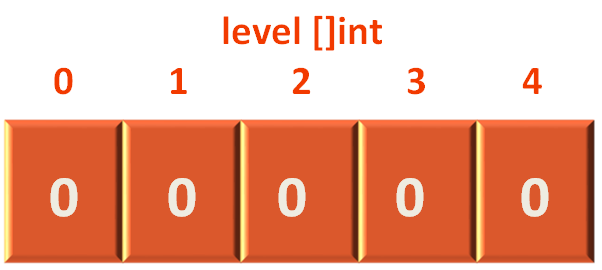
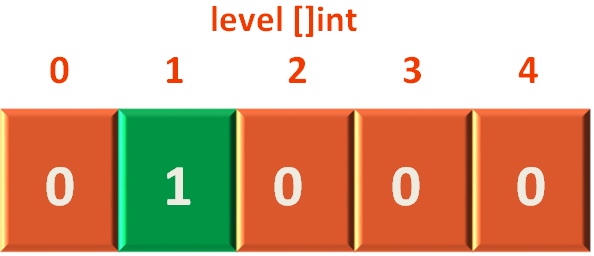
Lastly, we need the integer array to store the Levels, that is initialised with 0.

Now, since we have everything in place. Let us understand the func breadthFirstSearch(source string) method.

So, if we see the first line of the above method,

var queue []int

We have declared an Array that behaves as a Queue to maintain the order of Breadth First Search (BFS).

Next, we will try to find the index of the source vertex,

sourceIndex := sort.StringSlice(vertices).Search(source)

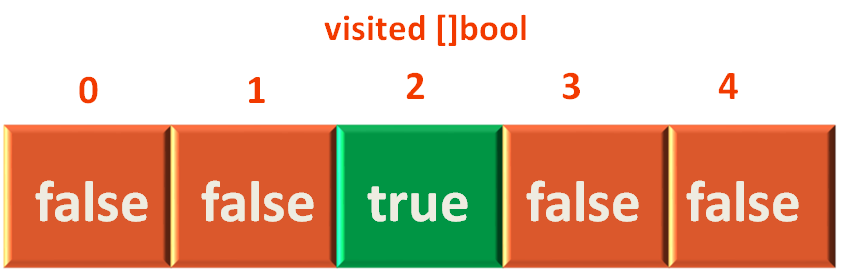
In this case our source vertex is c. i.e. We will start traversing the graph from c. And the index of vetex c is 2.

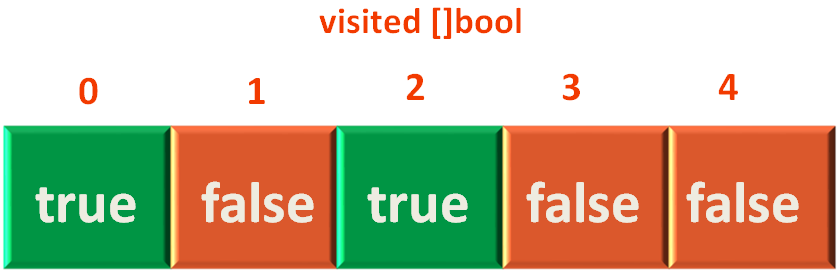
So, the next thing we will do is mark vertex c as visited. i.e. We will mark the position of Vertex c to true in the Visited Array.

visited[sourceIndex] = true

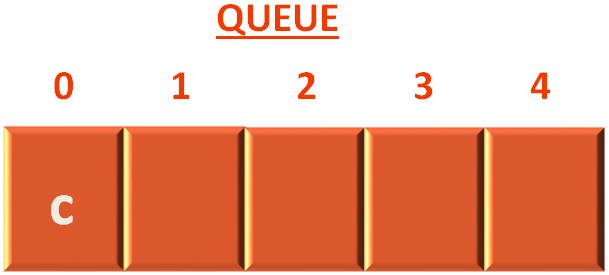
And add the vertex c to the Queue.

	queue = append(queue, sourceIndex)

Next, we come to the for() loop, that will continue until the Array that represents the Queue is not empty.

for len(queue) != 0 {

	sourceIndex = queue[0]

	// Slice off the element once it is dequeued.
	queue = queue[1:]

	for j := 0; j < len(adjacencyList[sourceIndex]); j++ {

		str := adjacencyList[sourceIndex][j]

		i := sort.StringSlice(vertices).Search(str);

		if (visited[i] == false) {

			visited[i] = true
			level[i] = level[sourceIndex] + 1

			queue = append(queue, i)
		}
	}
	fmt.Print(" --> ",vertices[sourceIndex]," of level ",level[sourceIndex])
}

Inside the for() loop, we write the below statement to get the vertex c out of the Queue and get its index in sourceIndex.

sourceIndex = queue[0]

The next task we do is, try finding the Adjacent Vertices of vertex c.

As we know the Adjacent Vertices of vertex c are,

To find the Adjacent Vertices of c, we have used the below for loop,

for j := 0; j < len(adjacencyList[sourceIndex]); j++

Inside the for loop, firstly we collect the first element(i.e. a) of the Adjacency List of vertex c.

str := adjacencyList[sourceIndex][j]

i.e.

adjacencyList[sourceIndex][j]
adjacencyList[2][0] (Since, sourceIndex is 2' )

So, str := 'a'

As we know the variable str contains a. Now, it's time to check the index of a.

Which we have done in the next line.

i := sort.StringSlice(vertices).Search(str)

And found that the index of a is 0.

Then in the next few lines, we check, if we have visited vertex a or not. So we check in the visited[] array.

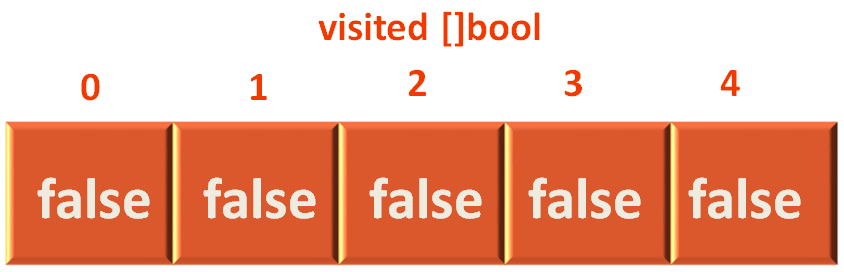
And find that visited[0] is set to false. So, we get into the below if condition.

if (visited[i] == false) {

	visited[i] = true
	level[i] = level[sourceIndex] + 1

	queue = append(queue, i)
}

Firstly, we mark visited[0] to true. Then increase the level[] array by 1.

And finally add the vertex a to the Queue.

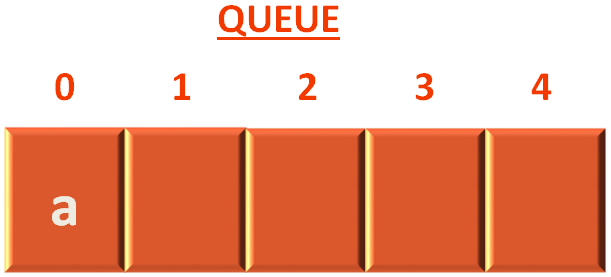
We keep on checking the adjacency lists of the individual vertices and continue the same process until the Queue is empty.

❮❮ PREV NEXT ❯❯