JAVA - SCRIPT-BREADTH FIRST SEARCH CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

<html>
<body>    
<script>

    function insertVertex(vertex) {
        vertices.push(vertex)
    }	

    function constructAdjacencyList(vtx, adjcVertex) {
        var vtxIndex = vertices.indexOf(vtx)
        adjacencyList.push([])
        adjacencyList[vtxIndex].push(adjcVertex)
    }	

    function breadthFirstSearch(source) {
        var queue = []
        var sourceIndex = vertices.indexOf(source)
        visited[sourceIndex] = true
        queue.push(sourceIndex)

        while (queue.length != 0) {
            sourceIndex = queue.shift()
            for (iter of adjacencyList[sourceIndex]) {
                var str = iter
                let i = vertices.indexOf(str)
                if (visited[i] == false) {
                    visited[i] = true
                    level[i] = level[sourceIndex] + 1
                    queue.push(i)
                }
            }		
            document.write(vertices[sourceIndex]," of level ",level[sourceIndex], " --> ")
        }	
        document.write("</br>")
    }	

    const V = 5
    var visited = new Array(V).fill(false)
    var level = new Array(V).fill(0)
    var adjacencyList = [[]]
    var vertices = []

    // Insert Vertices

    insertVertex("a")
    insertVertex("b")
    insertVertex("c")
    insertVertex("d")
    insertVertex("e")

    // Construct Adjacency List

    constructAdjacencyList("a", "b")
    constructAdjacencyList("a", "c")
    constructAdjacencyList("a", "d")

    constructAdjacencyList("b", "a")
    constructAdjacencyList("b" ,"e")

    constructAdjacencyList("c", "a")
    constructAdjacencyList("c", "d")
    constructAdjacencyList("c", "e")

    constructAdjacencyList("d", "a")
    constructAdjacencyList("d" ,"c")
    constructAdjacencyList("d", "e")

    constructAdjacencyList("e", "b")
    constructAdjacencyList("e", "c")
    constructAdjacencyList("e", "d")

    breadthFirstSearch("c")

</script>
</body>
</html>

Output :

c of level 0 --> a of level 1 --> d of level 1 --> e of level 1 --> b of level 2

Code Explanation for BFS - Breadth First Search

Let's list out, what all do we need to support Breadth First Search Data Structure.

We need a Linked List to store the vertices.

We need a doubly Linked List to store the adjacency linked list.

We need a Queue and an array to store its Levels.

We need a boolean array to store the Vertices that are already visited.

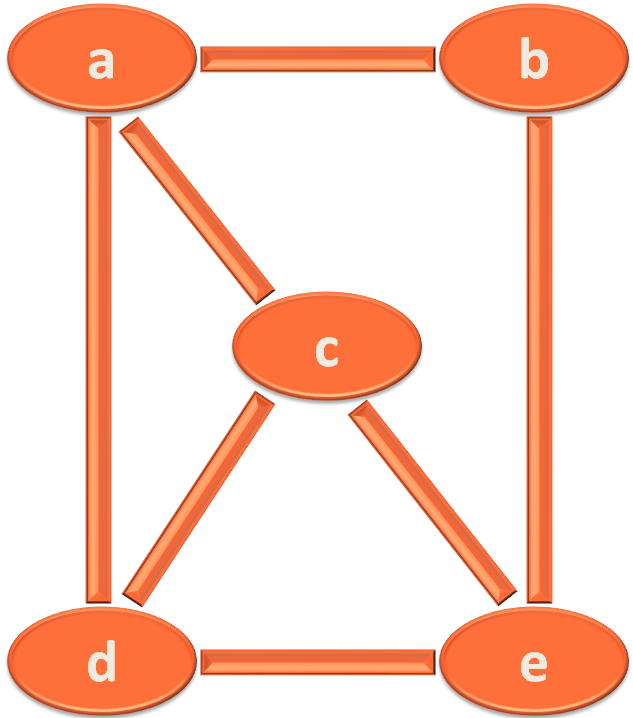
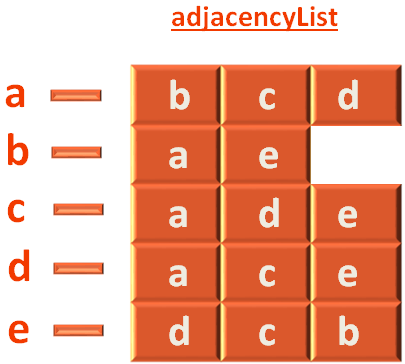
Now, let us see the above code.

We have a Linked List to store the Vertices.

var vertices = []

We also have a doubly Linked List to store the Adjacency List.

var adjacencyList = [[]]

Similarly, we have a Queue defined inside the method breadthFirstSearch(...).

var queue = []

And, we have an array to store the Levels.

var level = []

And, there is a boolean array to store the Vertices that are visited.

var visited = []

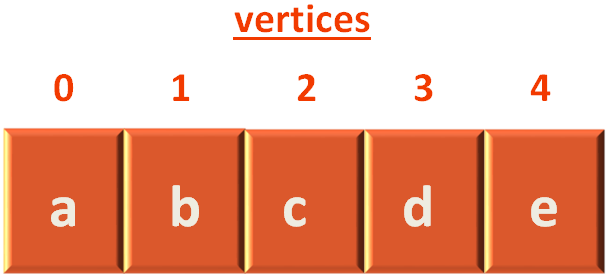
So, the first thing we will do is, insert the Vertices to the vertices Linked List.

var vertices = []

insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")

Explanation of function insertVertex(vertex) method

function insertVertex(vertex) {
	vertices.push(vertex)
}

function insertVertex(vertex) is quite simple.

There is just one statement in it.

vertices.push(vertex)

It accepts a string vertex as a parameter and adds it to the Linked List, vertices.

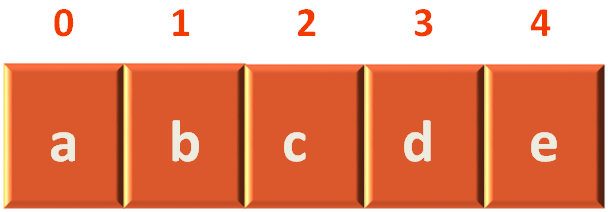
The next thing we will do is, create an Adjacency List to track the Adjacent Vertices.

Let us take the example of vertex a, to explain the creation of Adjacency List.

As we have seen, a has three adjacent vertices(i.e. b, c and d). And we have used the constructAdjacencyList(...) method to construct the Adjacency Matrix.

constructAdjacencyList("a", "b")
constructAdjacencyList("a", "c")
constructAdjacencyList("a", "d")

Note : Just remember, creating an Adjacency List above is same as creating an Edge. As the Adjacency List is actually a group of Edges.

Explanation of function constructAdjacencyList(vtx, adjcVertex) method

function constructAdjacencyList(vtx, adjcVertex) {
	var vtxIndex = vertices.indexOf(vtx)
	adjacencyList.push([])
	adjacencyList[vtxIndex].push(adjcVertex)
}

Although, the above method is explained in Adjacency List Code tutorial. I will give a brief explanation in this tutorial.

When a method call is made,

The variable vtx is assigned with value "a" and adjcVertex is assigned with "b".

Now, the first line,

vtxIndex = vertices.indexOf(vtx)

Calculates the index/position of Vertex a. And as we can see the index a is 0.

Now, in the next line,

adjacencyList.push([])

We are initialising the first row of the 2D Linked List, adjacencyList.

But with what?

We are initialising it with a Linked List [],

adjacencyList.push([]);

So that the first row can hold the Adjacency List for vertex a.

Similarly, the second row should hold the Adjacency List for vertex b and so on.

And in this iteration, our target is to find out the first row(To create an Adjacency List for vertex a) and insert vertex b to it.

And the below code does that.

adjacencyList[vtxIndex].push(adjcVertex)

We get the index of vertex a

vtxIndex = vertices.indexOf(vtx)

As we know vtx is a.

Then add adjcVertex(That contains vertex b) to the 0th index of adjacencyList.

adjacencyList[0].push("b")

And following it we form the Adjacency List.

Then we come across the most important method function breadthFirstSearch(source) that performs the Breadth First Search (BFS).

Explanation of function breadthFirstSearch(source) method

function breadthFirstSearch(source) {
	var queue = []
	var sourceIndex = vertices.indexOf(source)
	visited[sourceIndex] = true
	queue.push(sourceIndex)

	while (queue.length != 0) {
		sourceIndex = queue.shift()
		for (iter of adjacencyList[sourceIndex]) {
			var str = iter
			let i = vertices.indexOf(str)
			if (visited[i] == false) {
				visited[i] = true
				level[i] = level[sourceIndex] + 1
				queue.push(i)
			}
		}
		document.write(vertices[sourceIndex]," of level ",level[sourceIndex], " --> ")
	}
	document.write("
")
}

So, we are calling the method

breadthFirstSearch("c")

Passing the vertex c as source.

Below is the graph on which we had to perform a Breadth First Search (BFS).

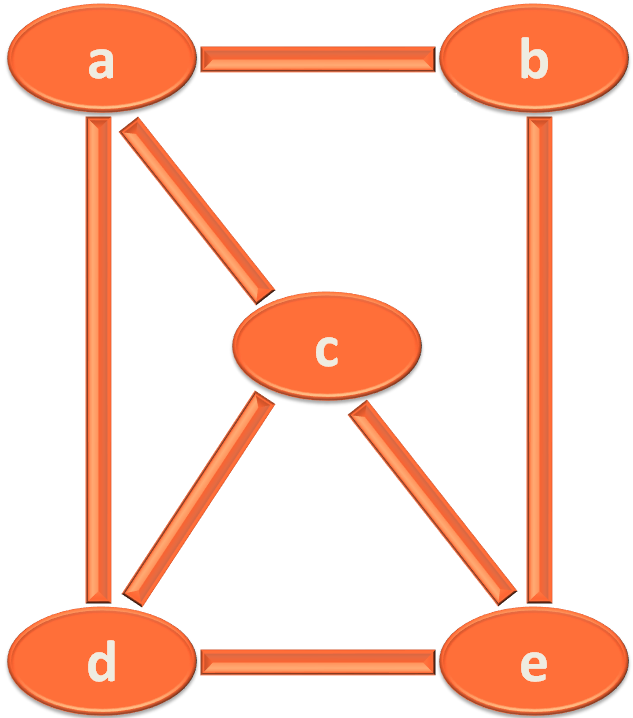
To perform Breadth First Search (BFS), all we need is a Linked List to keep track of Vertices. Which we have in place.

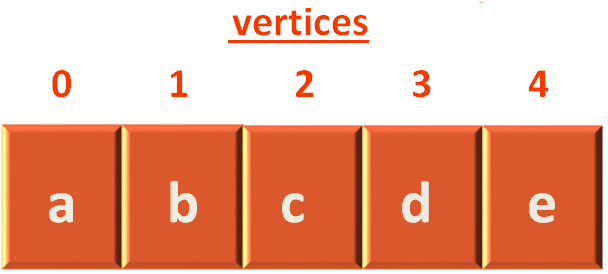
And, we need a 2D Adjacency List to keep a track of Adjacent Vertices. And we also have that in place.

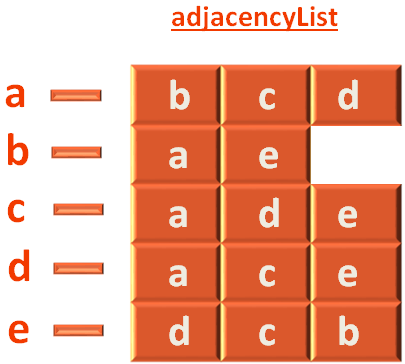
We also need a boolean array to keep a track of which all vertices are visited. Which we also have in place. All the values default to false.

Lastly, we need the integer array to store the Levels, that is initialised with 0.

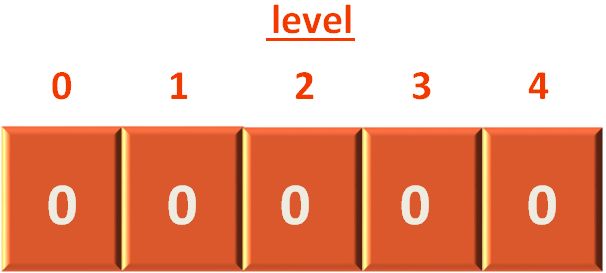
Now, since we have everything in place. Let us understand the function breadthFirstSearch(...) method.

So, if we see the first line of the above method,

queue = []

We have declared the Queue to maintain the order of Breadth First Search (BFS).

Next, we will try to find the index of the source vertex,

sourceIndex = vertices.indexOf(source)

In this case our source vertex is c. i.e. We will start traversing the graph from c. And the index of vetex c is 2.

So, the next thing we will do is mark vertex c as visited. i.e. We will mark the position of Vertex c to true in the Visited Array.

visited[sourceIndex] = true

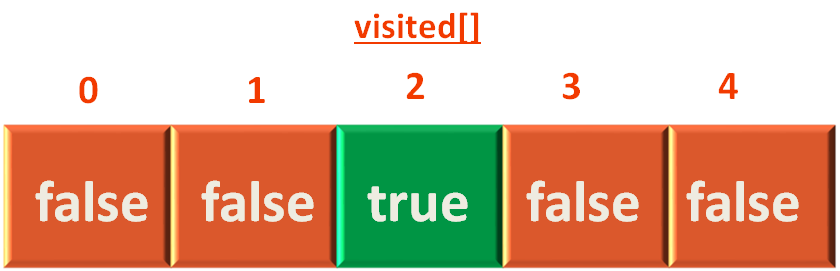
And add the vertex c to the Queue.

	queue.push(sourceIndex)

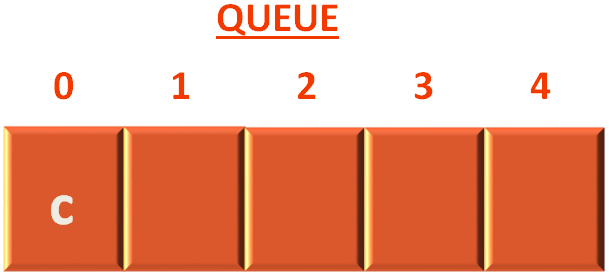
Next, we come to the while() loop, that will continue until the Queue is not empty.

while (queue.length != 0) {
	sourceIndex = queue.shift()
	for (iter of adjacencyList[sourceIndex]) {
		var str = iter
		let i = vertices.indexOf(str)
		if (visited[i] == false) {
			visited[i] = true
			level[i] = level[sourceIndex] + 1
			queue.push(i)
		}
	}
	document.write(vertices[sourceIndex]," of level ",level[sourceIndex], " --> ")
}

Inside the while() loop, we write the below statement to get the vertex c out of the Queue and get its index in sourceIndex.

sourceIndex = queue.shift()

The next task we do is, try finding the Adjacent Vertices of vertex c.

As we know the Adjacent Vertices of vertex c are,

To find the Adjacent Vertices of c, we have used the below for loop,

for (iter of adjacencyList[sourceIndex])

And the for loop itself needs a little explanation.(HIDE THE BELOW POINTS UNDER DROPDOWN)

The first statement of the for loop (i.e. The initialisation section of the loop),
```
for (iter of adjacencyList[sourceIndex])
```
is where we get the Adjacent Vertices of vertex c in the iter.

Thinking How?

Well! The adjacencyList is a 2D Linked List that stores the adjacent vertices. And the trick is played in,
```
adjacencyList[sourceIndex]
```
As we have seen, the sourceIndex is 2 (Because the index of vertex c is 2).

And the iter variable of iter gets the adjacency list of vertex c in it.

Moral of the story

iter variable of iter, stores the Adjacency List of vertex c in it.So, iter has the elements a, d and e in it.

Inside the for loop, firstly we collect the first element(i.e. a) of the Adjacency List of vertex c.

str = iter

As we know the variable str contains a. Now, it's time to check the index of a.

Which we have done in the next line.

i = vertices.indexOf(str)

And found that the index of a is 0.

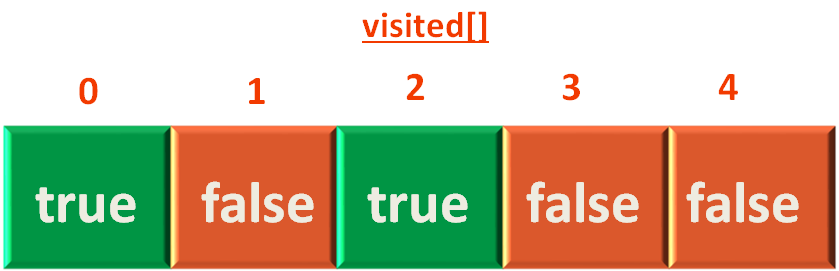
Then in the next few lines, we check, if we have visited vertex a or not. So we check in the visited[] array.

And find that visited[0] is set to false. So, we get into the below if condition.

if (visited[i] == false) {
	visited[i] = true
	level[i] = level[sourceIndex] + 1
	queue.push(i)
}

Firstly, we mark visited[0] to true. Then increase the level[] array by 1.

And finally add the vertex a to the Queue.

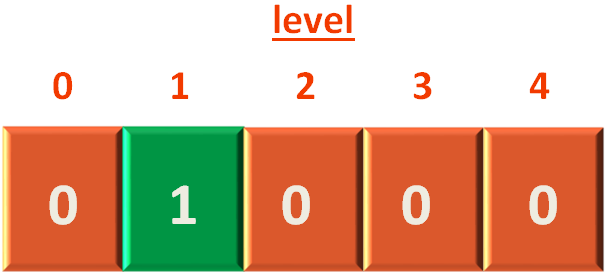
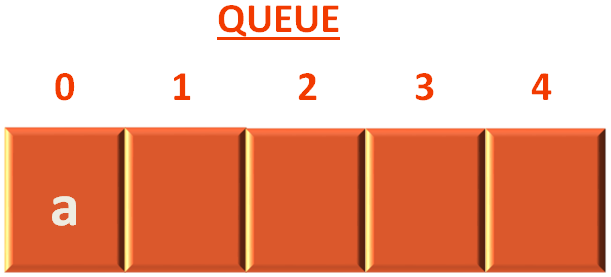
We keep on checking the adjacency lists of the individual vertices and continue the same process until the Queue is empty.

❮❮ PREV NEXT ❯❯