We will be seeing the Iterative way for implementing Depth First Search (DFS). Although there are various ways to write this Iterative code.
However, we will write the code little differently. So that you can corelate it with the Depth First Search (DFS) explanation.
In the Iterative code we will create the stack and maintain it ourselves.
package main
import "fmt"
import "sort"
var vertices []string
var adjacencyList [][]string
var visited []bool
func insertVertex(vertex string) {
vertices = append(vertices, vertex)
}
func constructTempList(tmpList *[]string, val string) {
*tmpList = append(*tmpList, val)
}
func constructAdjacencyList(adjcList *[][]string, tmpList *[]string) {
*adjcList = append(*adjcList, *tmpList)
*tmpList = nil
}
func depthFirstSearch(source string){
sourceIndex := sort.StringSlice(vertices).Search(source)
visited[sourceIndex] = true
var stack[]string
stack = append(stack, source)
fmt.Print(source)
for len(stack) != 0 {
index := len(stack) - 1 // Get the index of the top element
source := stack[index] // Get that element in that index
sourceIndex = sort.StringSlice(vertices).Search(source)
str := ""
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}
indexNew := len(stack) - 1 // Get the index of the top most element.
top := stack[indexNew]
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}
}
fmt.Println()
}
func main() {
const V = 6
var tempList[]string
visited = make([]bool, V)
// Adding vertices one by one
insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")
insertVertex("f")
// Create Adjacency List
constructTempList(&tempList, "c")
constructTempList(&tempList, "d")
constructAdjacencyList(&adjacencyList, &tempList)
constructTempList(&tempList, "d")
constructTempList(&tempList, "e")
constructTempList(&tempList, "c")
constructAdjacencyList(&adjacencyList, &tempList)
constructTempList(&tempList, "a")
constructTempList(&tempList, "b")
constructTempList(&tempList, "e")
constructAdjacencyList(&adjacencyList, &tempList)
constructTempList(&tempList, "a")
constructTempList(&tempList, "b")
constructTempList(&tempList, "e")
constructTempList(&tempList, "f")
constructAdjacencyList(&adjacencyList, &tempList)
constructTempList(&tempList, "b")
constructTempList(&tempList, "c")
constructTempList(&tempList, "d")
constructTempList(&tempList, "f")
constructAdjacencyList(&adjacencyList, &tempList)
constructTempList(&tempList, "d")
constructTempList(&tempList, "e")
constructAdjacencyList(&adjacencyList, &tempList)
depthFirstSearch("a")
}
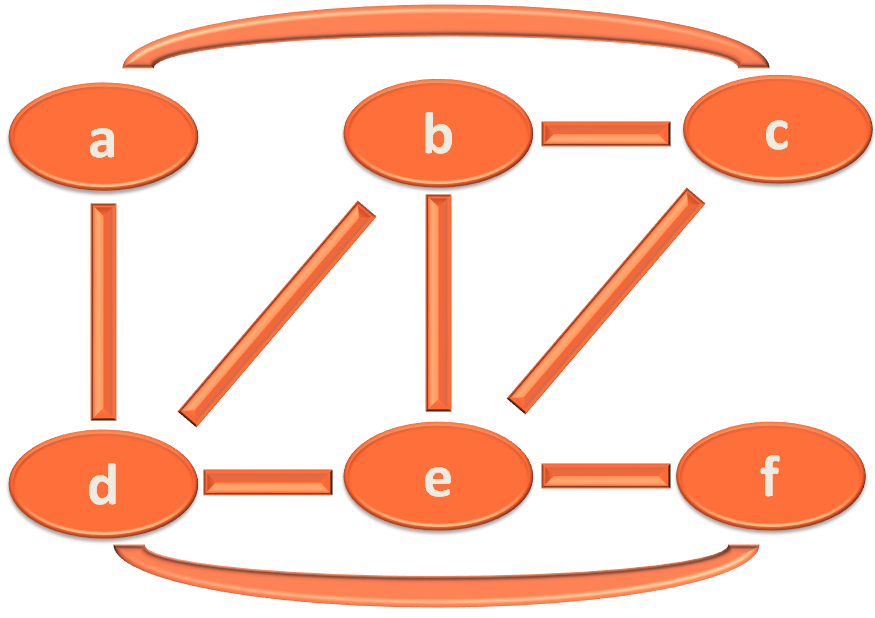
We have implemented Depth First Search (DFS) on the below graph :
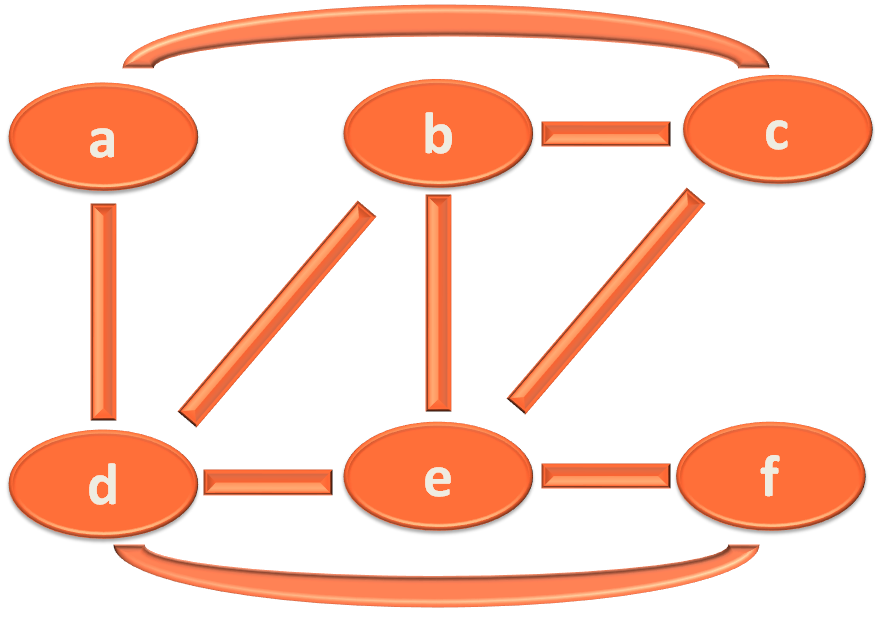
We can take various ways to navigate the graph using Depth First Search (DFS). Just remember our main intension is to visit all the vertices.
In this case we have covered the graph in the following path :
a --> c --> b --> d --> e --> f
Let us see how ?
Below code explains the methods :
Almost the same we have discussed in BFS. You can skip it if you wane to.
Click Here - To understand the details of the methods 'func constructAdjacencyList(adjcList *[][]string, tmpList *[]string)' and 'func constructTempList(tmpList *[]string, val string)'.
Let's list out, what all do we need to support Depth First Search Data Structure.
Now, let us see the above code.
We have an Array to store the Vertices.
var vertices []string
We also have a doubly Linked List to store the Adjacency List.
var adjacencyList [][]string
Similarly, we have a stack defined inside the method depthFirstSearch(...).
var stack[]string
And, there is a boolean array to store the Vertices that are visited.
var visited []bool
So, the first thing we will do is, insert the Vertices to the Array var vertices []string.
insertVertex("a")
insertVertex("b")
insertVertex("c")
insertVertex("d")
insertVertex("e")
insertVertex("f")func insertVertex(vertex string) {
vertices = append(vertices, vertex)
}func insertVertex(vertex string) is quite simple.
There is just one statement in it.
vertices = append(vertices, vertex)
It accepts vertex string as a parameter and adds it to the Array, vertices.
The next thing we will do is, create an Adjacency List to track the Adjacent Vertices.
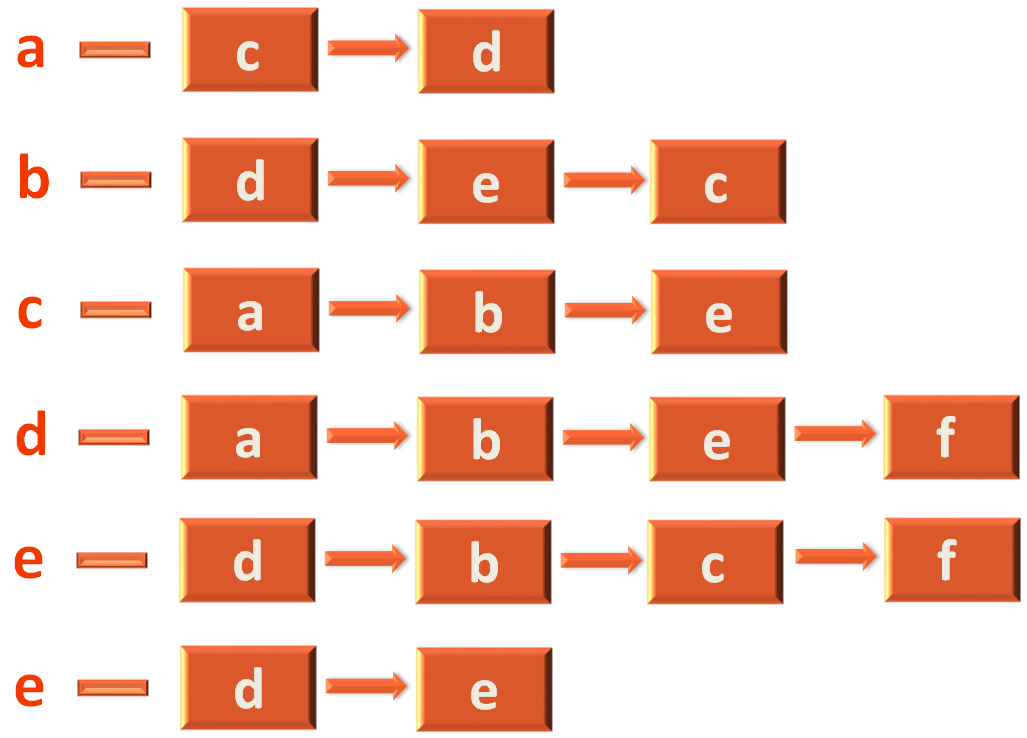
Let us take the example of vertex a, to explain the creation of Adjacency List.
As we have seen, a has two adjacent vertices(i.e. c and d). And we have used the constructTempList(...) method to construct the Adjacency List.
constructTempList(&tempList, "c") constructTempList(&tempList, "d")
And add the tempList[] Array with adjacent vertices to the Adjacency List Array var adjacencyList [][]string.
constructAdjacencyList(&adjacencyList, &tempList)
func constructAdjacencyList(adjcList *[][]string, tmpList *[]string) {
*adjcList = append(*adjcList, *tmpList)
*tmpList = nil
}Initially, we create a tmpList[] Array. That would just hold the adjacent vertices of one node temporarily.
constructTempList(&tempList, "c") constructTempList(&tempList, "d")

Then we take the tempList[] Array and pass it to the func constructAdjacencyList(...).
constructAdjacencyList(&adjacencyList, &tempList)
And in the first line itself,
*adjcList = append(*adjcList, *tmpList)
We are adding the contents of tempList[] array to the first row of adjcList[][] array.
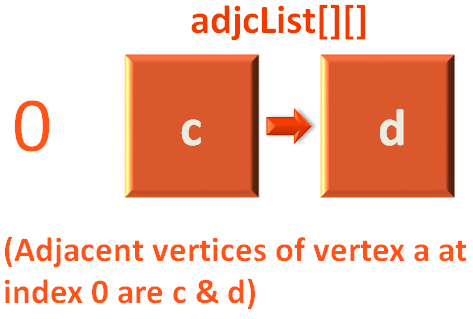
So that the first row can hold the Adjacency List for vertex a.

Now, we come across the most important method func depthFirstSearch(source string) that performs the Depth First Search (DFS).
func depthFirstSearch(source string){
sourceIndex := sort.StringSlice(vertices).Search(source)
visited[sourceIndex] = true
var stack[]string
stack = append(stack, source)
fmt.Print(source)
for len(stack) != 0 {
index := len(stack) - 1 // Get the index of the top element
source := stack[index] // Get that element in that index
sourceIndex = sort.StringSlice(vertices).Search(source)
str := ""
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}
indexNew := len(stack) - 1 // Get the index of the top most element.
top := stack[indexNew]
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}
}
fmt.Println()
}We have called the func depthFirstSearch(source string) from the main method passing a as the parameter.
depthFirstSearch("a")So, the first thing we will do in func depthFirstSearch(source string) is, take the index of a,
sourceIndex := sort.StringSlice(vertices).Search(source)
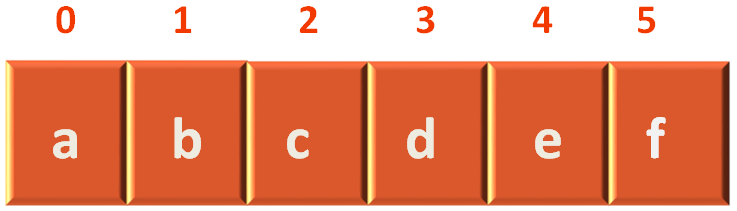
Now, if we see the List of vertices,
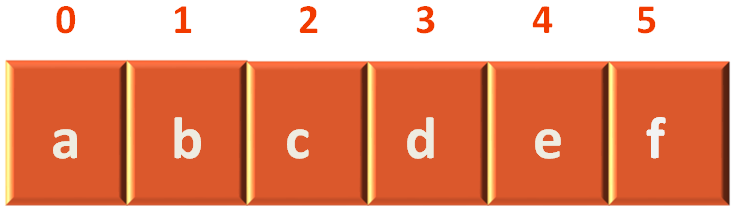
We can see that a lies in index 0.
Next, we mark a as visited,
visited[sourceIndex] = true
in the visited[] array,
visited[0] = true
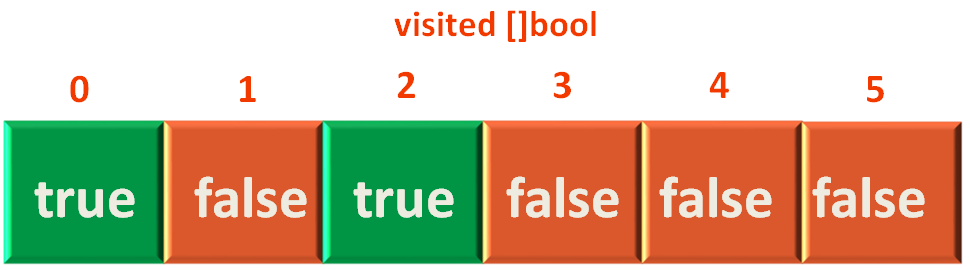
Then, we create the stack,
var stack[]string
And the immediate next thing we do is, push a to the stack.
stack = append(stack, source)
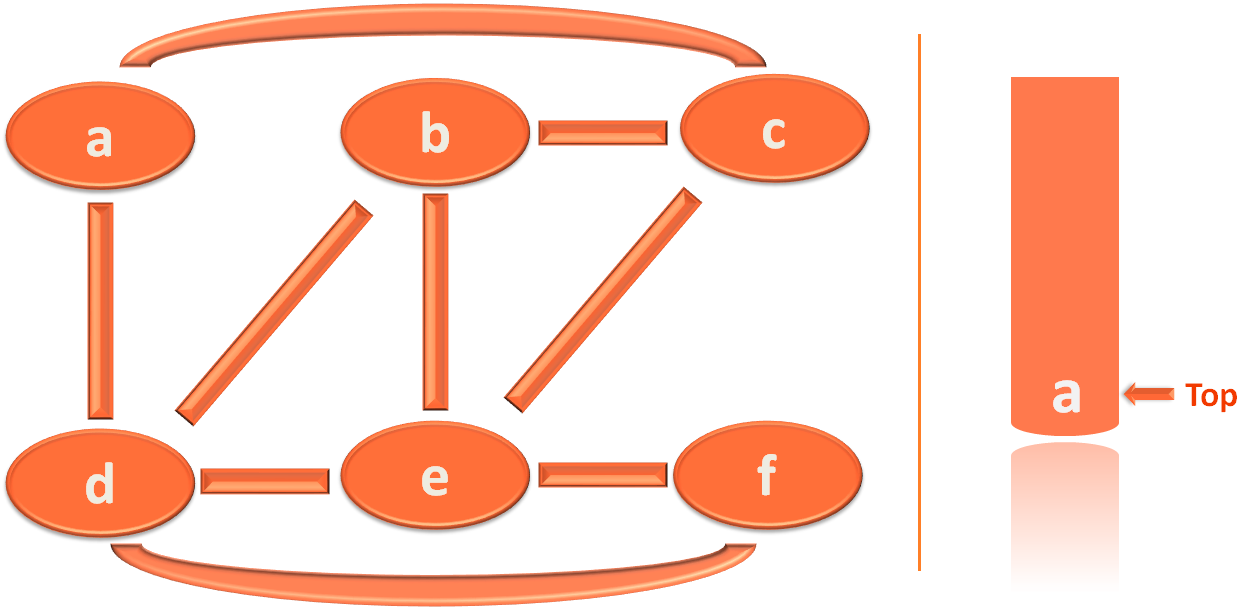
Then we print the vertex a.
fmt.Print(source)
Next, we enter the for() loop that continues until the stack is not empty.
for len(stack) != 0 {
index := len(stack) - 1 // Get the index of the top element
source := stack[index] // Get that element in that index
sourceIndex = sort.StringSlice(vertices).Search(source)
str := ""
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}
indexNew := len(stack) - 1 // Get the index of the top most element.
top := stack[indexNew]
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}
}In the outer for() loop, we take the top element(i.e. a) in the source variable.
index := len(stack) - 1 // Get the index of the top element source := stack[index] // Get that element in that index
The we take the index of the top element(0 is the index of a).
sourceIndex = vertices.indexOf(source);
Then comes the inner for(...) loop, where we find the adjacent vertices of the top element(i.e. a).
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}Now, in the first line, we have str that contains the first adjacent vertex c.
str = adjacencyList[sourceIndex][j]
Next, we find the index of vertex c,
i := sort.StringSlice(vertices).Search(str)
Now, if we see the List of vertices,
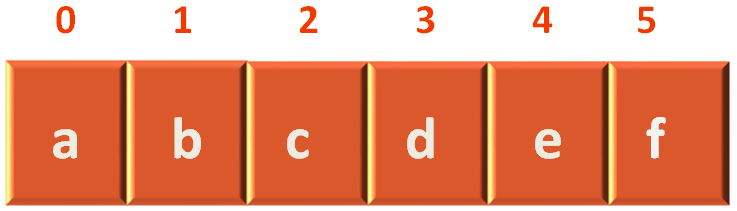
We can see that c lies in index 2.
So, we check if c is visited or not.
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}Now, if we check the visited array,

We found that visited[2] = false and we get into the if statement.
So, we push c to the Queue.
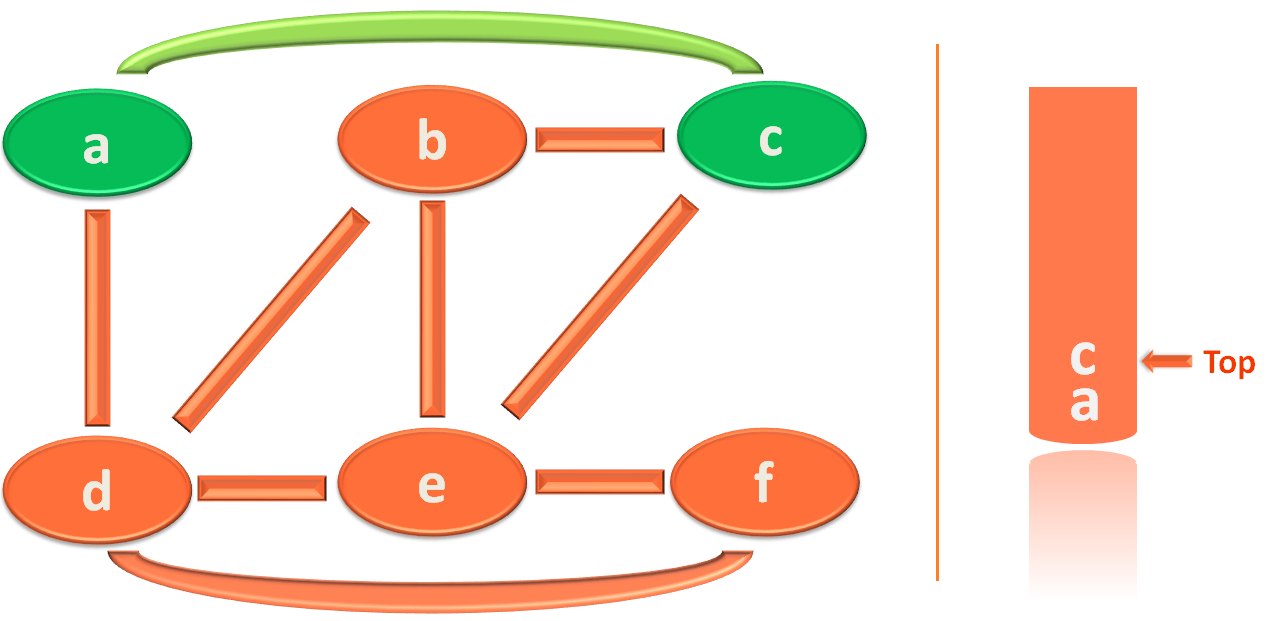
And marked visited[2] = true,
visited[i] = true;
In the visited[] array,
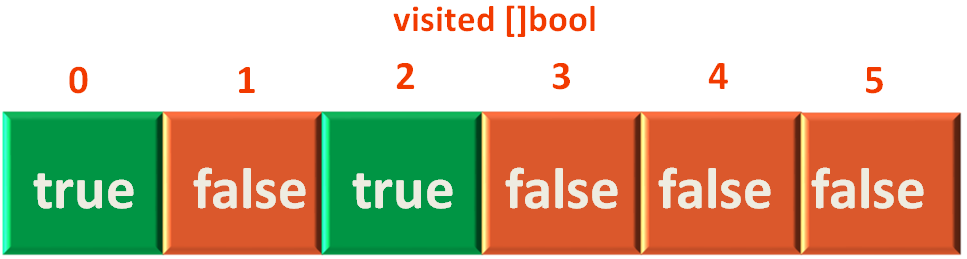
then we break out of the for loop
break
After getting out of the for loop, we get the top element from the stack.
indexNew := len(stack) - 1 // Get the index of the top most element. top := stack[indexNew]
Then we check if the value inside the str variable and the top element are equal or not.
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}In this case str has c inside it and the top element of the stack is also c.
So, we don't pop c out of the stack and continue with the while loop.
Similarly, we repeat the same process until all the vertices are visited.
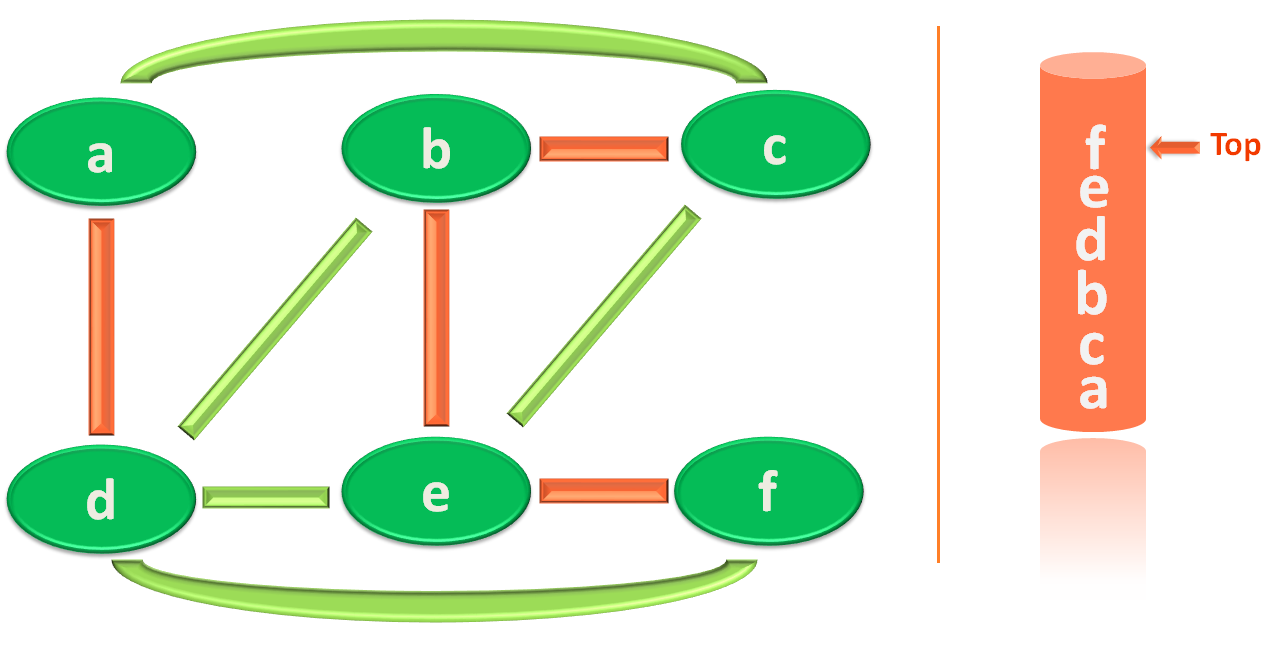
Now, let's visit the outer for() loop again.
for len(stack) != 0 {
index := len(stack) - 1 // Get the index of the top element
source := stack[index] // Get that element in that index
sourceIndex = sort.StringSlice(vertices).Search(source)
str := ""
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}
indexNew := len(stack) - 1 // Get the index of the top most element.
top := stack[indexNew]
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}
}The top element is f now,
index := len(stack) - 1 // Get the index of the top element source := stack[index] // Get that element in that index
So, the value of source variable is f and
sourceIndex = sort.StringSlice(vertices).Search(source)
the value of sourceIndex variable would be 5.
Now, the adjacent vertices of f are d and e.
for j := 0; j < len(adjacencyList[sourceIndex]); j++ {
str = adjacencyList[sourceIndex][j]
i := sort.StringSlice(vertices).Search(str)
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}
}So, the variable str would contain d(Since, the adjacent vertices of f are d and e) in the first iteration and would be e in the second iteration.
str = adjacencyList[sourceIndex][j] i := sort.StringSlice(vertices).Search(str)
And both e and d are visited. So, the lines under the if statement are never visited.
if (visited[i] == false) {
stack = append(stack, str)
visited[i] = true
fmt.Print(" --> ",str)
break
}So, the for loop completes. And the value of the variable str would be e.
So, after getting out of the for loop, we check if the value inside the str variable and the top element are equal or not.
indexNew := len(stack) - 1 // Get the index of the top most element.
top := stack[indexNew]
if (top != str){
//Pop operation
stack = stack[:indexNew] // Remove it from the stack
}In this case the top element is f and the value in str is e.
And the if (top != str) condition matches and f is popped out of the queue.
stack = stack[:indexNew] // Remove it from the stack

Continuing in the same way, all the elements are popped out of the Queue and the execution ends.