RUBY - AVL TREES CODE

JAVA PYTHON GO KOTLIN C# RUBY C++ Java Script

Example :

class Node
	attr_accessor :data, :left, :right, :height, :size
	
    def initialize(data)
        @data = data
        @left = nil
        @right = nil
        @height = 1
		@size = 0
    end
end        


class TreeTraversal
	def initialize()
		@root = nil
	end	

	def inOrder(node)
		if (node != nil)
			inOrder(node.left)
			print(node.data, "  ")
			inOrder(node.right)
		end
	end
end		

def leftRotate(rootNode)
	newRoot = rootNode.right
	rootNode.right = rootNode.right.left
	newRoot.left = rootNode
	rootNode.height = setHeight(rootNode)
	rootNode.size = setSize(rootNode)
	newRoot.height = setHeight(newRoot)
	newRoot.size = setSize(newRoot)
	return newRoot
end	

def rightRotate(rootNode)
	newRoot = rootNode.left
	rootNode.left = rootNode.left.right
	newRoot.right = rootNode
	rootNode.height = setHeight(rootNode)
	rootNode.size = setSize(rootNode)
	newRoot.height = setHeight(newRoot)
	newRoot.size = setSize(newRoot)
	return newRoot
end	

def setSize(rootNode)
	if(rootNode == nil)
		return 0
	end	
	return 1 + [(rootNode.left != nil ? rootNode.left.size : 0), (rootNode.right != nil ? rootNode.right.size : 0)].max
end

def insert(rootNode, data)
	if (rootNode == nil)
		rootNode = Node.new(data)
		return rootNode
	end

	if (data < rootNode.data)
		rootNode.left = insert(rootNode.left, data)
	elsif (data > rootNode.data)
		rootNode.right = insert(rootNode.right, data)
	end	

	balanceFactor = balance(rootNode.left, rootNode.right)

	if(balanceFactor > 1)
		if(height(rootNode.left.left) >= height(rootNode.left.right))
			rootNode = rightRotate(rootNode)
		else
			rootNode.left = leftRotate(rootNode.left)
			rootNode = rightRotate(rootNode)
		end	
	elsif(balanceFactor < -1)
		if(height(rootNode.right.right) >= height(rootNode.right.left))
			rootNode = leftRotate(rootNode)
		else
			rootNode.right = rightRotate(rootNode.right)
			rootNode = leftRotate(rootNode)
		end	
	else
		rootNode.height = setHeight(rootNode)
		rootNode.size = setSize(rootNode)
	end	
	return rootNode
end	

def balance(rootNodeLeft, rootNodeRight)
	return height(rootNodeLeft) - height(rootNodeRight)
end	

def setHeight(rootNode)
	if(rootNode == nil)
		return 0
	end	
	return 1 + [(rootNode.left != nil ? rootNode.left.height : 0), (rootNode.right != nil ? rootNode.right.height : 0)].max
end

def height(rootNode)
	if(rootNode == nil)
		return 0
	else
		return rootNode.height
	end
end	


root = nil
root = insert(root, 16)
root = insert(root, 10)
root = insert(root, 25)
root = insert(root, 2)
root = insert(root, 13)
root = insert(root, 18)
root = insert(root, 30)
root = insert(root, 7)
root = insert(root, 8)

tt = TreeTraversal.new()
print("Inorder Traversal : \n")
tt.inOrder(root)

puts

Output :

Inorder Traversal :
2 7 8 10 13 16 18 25 30

Code Explanation

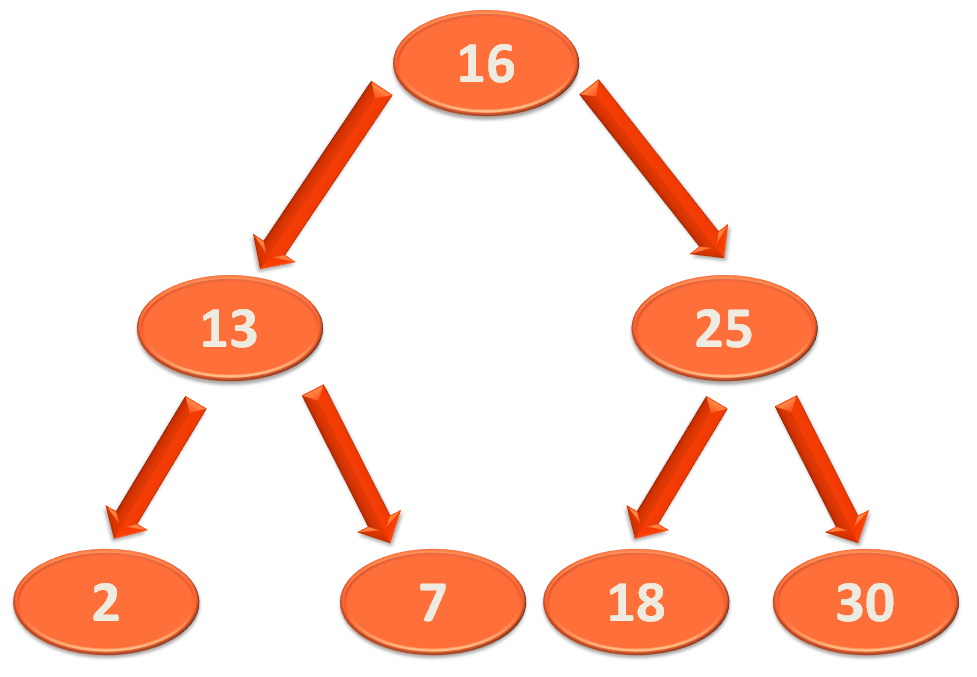
So, we will constructing the below Balanced Binary Search Tree, by inserting the elements one by one.

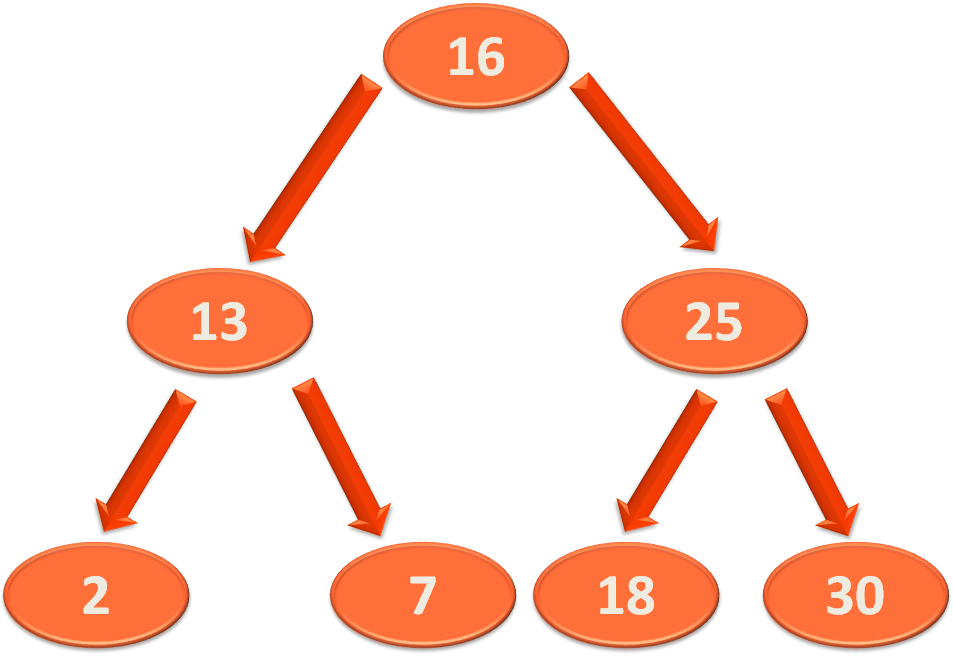
And we have the below methods :

def insert(root, key)

This method is used to insert a new Node to the Binary Search Tree. Then balance it as per the rules of AVL Tree.

def leftRotate(rootNode)

This method is used to Left Rotate the Binary Search Tree in order to balance it as per the rules of AVL Tree.

def rightRotate(rootNode)

This method is used to Right Rotate the Binary Search Tree in order to balance it as per the rules of AVL Tree.

def balance(rootNodeLeft, rootNodeRight)

As the name suggests, this method is used to balance the Binary Search Tree as per the rules of AVL Tree.

def setHeight(rootNode) and def height(rootNode)

As we know an AVL Tree is a height balanced Binary Search Tree. And the setHeight(...) and height(...) are the methods where the height of the AVL Tree is calculated.

Code explanation for AVL Tree :

Firstly, we would be constructing the above Binary Search Tree, with the help of insert method.

root = nil
root = insert(root, 16)

Initially, the variable root is nil. So, we take the element i.e. 16 in this case. And pass the root and the element 16 to the insert method.

def insert(rootNode, data) method

def insert(rootNode, data)
	if (rootNode == nil)
		rootNode = Node.new(data)
		return rootNode
	end

	if (data < rootNode.data)
		rootNode.left = insert(rootNode.left, data)
	elsif (data > rootNode.data)
		rootNode.right = insert(rootNode.right, data)
	end

	balanceFactor = balance(rootNode.left, rootNode.right)

	if(balanceFactor > 1)
		if(height(rootNode.left.left) >= height(rootNode.left.right))
			rootNode = rightRotate(rootNode)
		else
			rootNode.left = leftRotate(rootNode.left)
			rootNode = rightRotate(rootNode)
		end
	elsif(balanceFactor < -1)
		if(height(rootNode.right.right) >= height(rootNode.right.left))
			rootNode = leftRotate(rootNode)
		else
			rootNode.right = rightRotate(rootNode.right)
			rootNode = leftRotate(rootNode)
		end
	else
		rootNode.height = setHeight(rootNode)
		rootNode.size = setSize(rootNode)
	end
	return rootNode
end

The first line of the insert(...) checks if the rootNode is nil or not.

if (rootNode == nil)
	rootNode = Node.new(data)
	return rootNode
end

And in this case rootNode is nil. So, we create a new Node object with the data i.e. 16. And the Node object is created with the below constructor.

def initialize(data)
	@data = data
	@left = nil
	@right = nil
	@height = 1
	@size = 0
end

Then assign it to the Node object root.

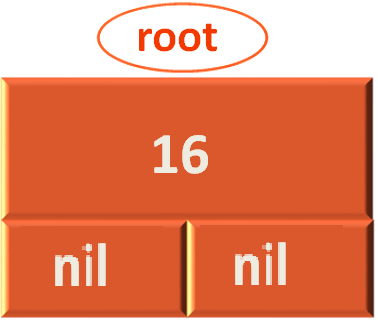
And return the Node root.

return root

In the next line we try to insert the element 13 in the Binary Search Tree using the insert(...) method.

root = insert(root, 10)

And the insert(...) method is called.

And in the similar way we check,

if (data < rootNode.data)
	rootNode.left = insert(rootNode.left, data)
elsif (data > rootNode.data)
	rootNode.right = insert(rootNode.right, data)
end

If the data i.e. 13 is less than the root element root.data. And the first condition matches.

if (data < rootNode.data)
	rootNode.left = insert(rootNode.left, data)

And a recursive call is made to insert(...) method.

rootNode.left = insert(rootNode.left, data)

So, the method executes and sets the value of rootNode.left with this Node that contains 13.

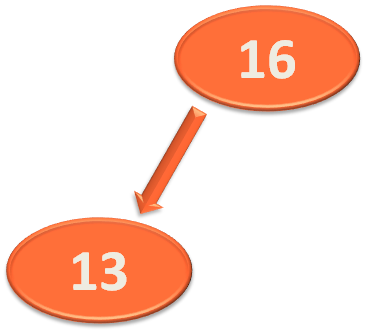
And since we are dealing with AVL tree, it is time to calculate the Balance Factor.

balanceFactor = balance(rootNode.left, rootNode.right)

And the balance(...) method is called.

def balance(rootNodeLeft, rootNodeRight)
	return height(rootNodeLeft) - height(rootNodeRight)
end

And the balance(...) method is quite simple to understand. It calls the height(...) method for the Left Node and Right Node and calculates the difference between Left and Right Node.

And as we know, Balance Factor is the difference of Left and Right Node.

And now since we got the Balance Factor, we need to perform Left or Right rotation if the value of Balance Factor is other than -1, 0 or 1.

if(balanceFactor > 1)
	if(height(rootNode.left.left) >= height(rootNode.left.right))
		rootNode = rightRotate(rootNode)
	else
		rootNode.left = leftRotate(rootNode.left)
		rootNode = rightRotate(rootNode)
	end
elsif(balanceFactor < -1)
	if(height(rootNode.right.right) >= height(rootNode.right.left))
		rootNode = leftRotate(rootNode)
	else
		rootNode.right = rightRotate(rootNode.right)
		rootNode = leftRotate(rootNode)
	end
else
	rootNode.height = setHeight(rootNode)
	rootNode.size = setSize(rootNode)
end

So, if the Balance Factor is greater than 1.

if(balanceFactor > 1)
	if(height(rootNode.left.left) >= height(rootNode.left.right))
		rootNode = rightRotate(rootNode)
	else
		rootNode.left = leftRotate(rootNode.left)
		rootNode = rightRotate(rootNode)
	end

We go to the left child of the rootNode and try checking, if the height of the left child of the left node is greater than the height of the right child of the left node.

if(height(rootNode.left.left) >= height(rootNode.left.right))
	rootNode = rightRotate(rootNode)

If the above condition satisfies, then we can assume that we need to right rotate the tree.

And the rightRotate(...) method is called to balance the tree.

def rightRotate(rootNode)
	newRoot = rootNode.left
	rootNode.left = rootNode.left.right
	newRoot.right = rootNode
	rootNode.height = setHeight(rootNode)
	rootNode.size = setSize(rootNode)
	newRoot.height = setHeight(newRoot)
	newRoot.size = setSize(newRoot)
	return newRoot
end

Let us take the below example to understand the rightRotate(...) method.

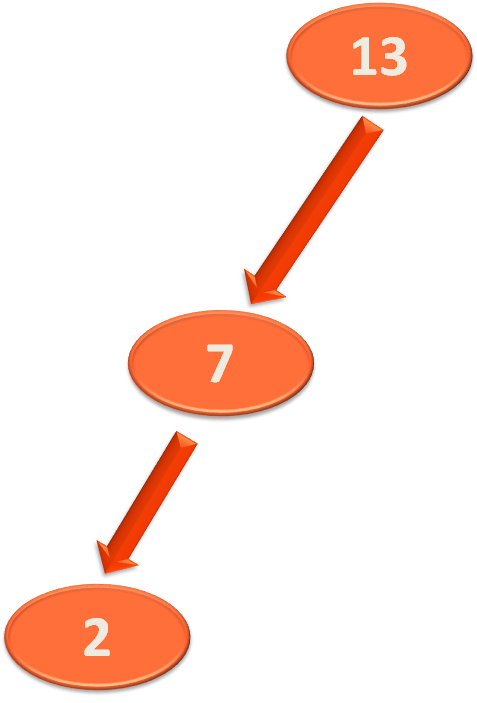
Say, rootNode has the element 13.

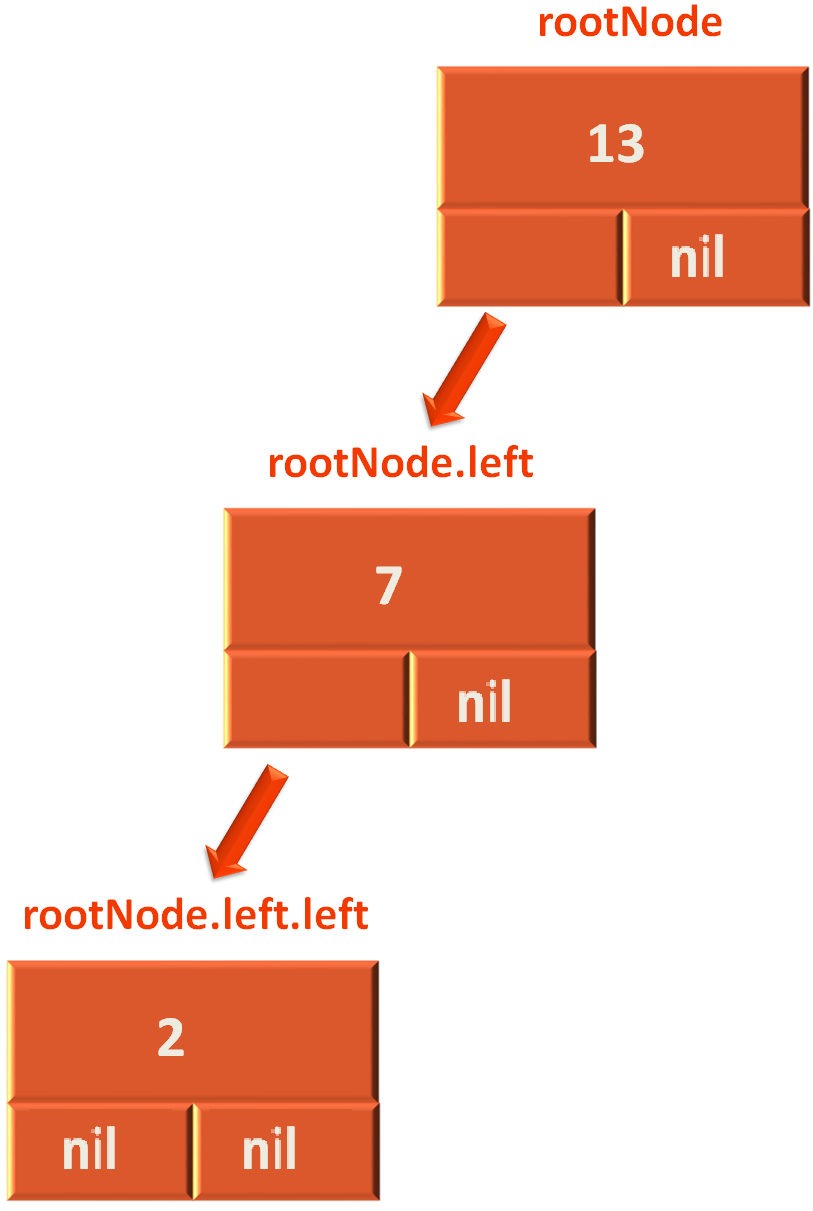
Now, we create a Node named newNode and assign the Node rootNode.left to it.

newRoot = rootNode.left

And as we can see in the above diagram rootNode.left has the element 7 in it.

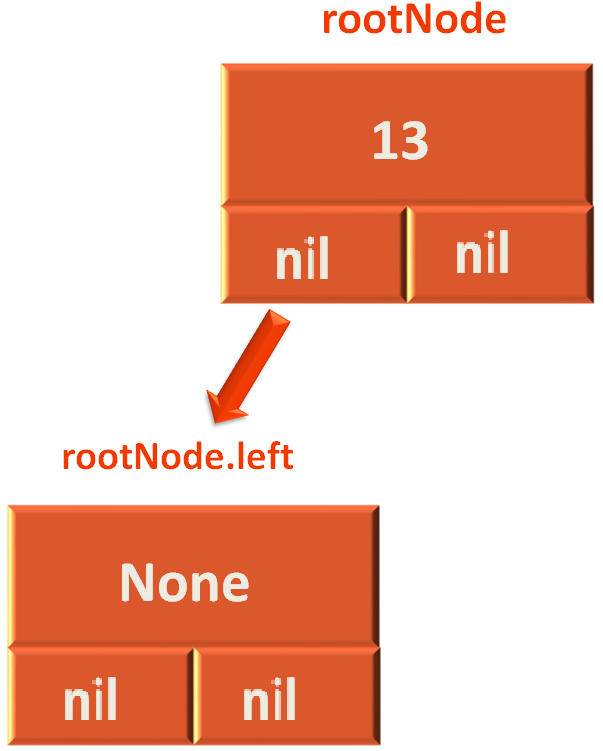
Then we take the rootNode.left.right (i.e. The right child of 7, which is nil in the above case) and assign it to rootNode.left.

rootNode.left = rootNode.left.right

And the below tree looks like,

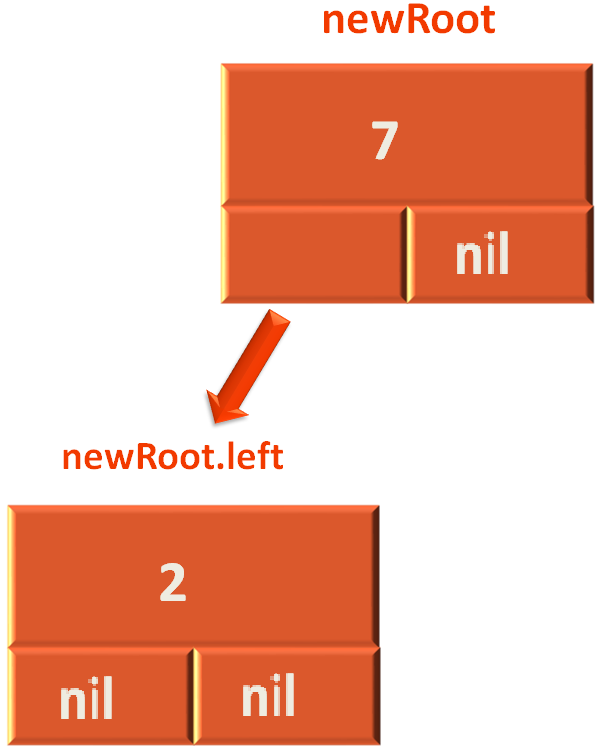
Next, we take the rootNode and assign it as the right child of the newly created Node newRoot.

newRoot.right = rootNode

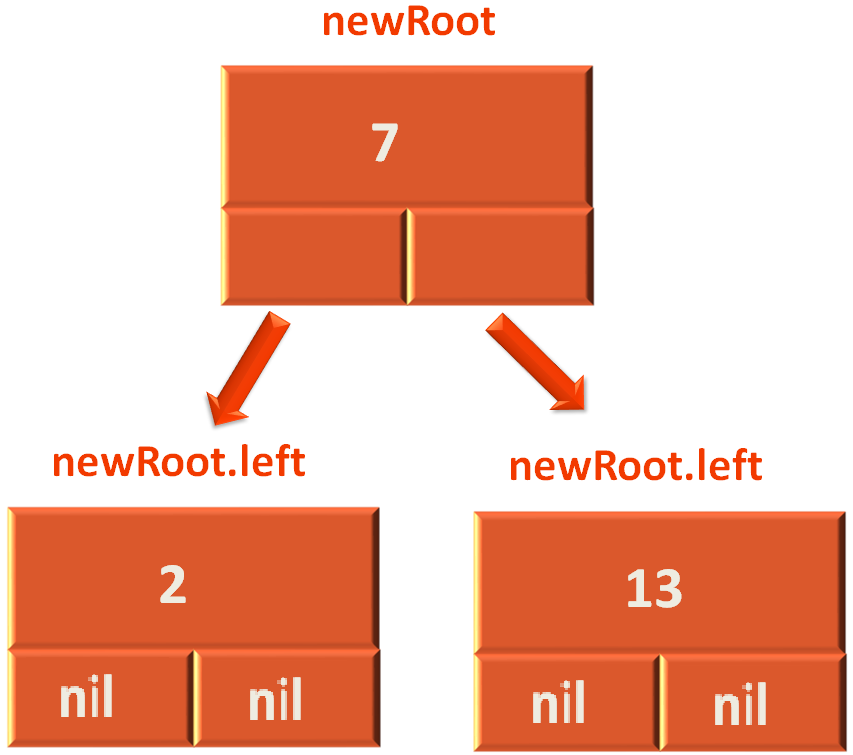
So, the right rotation is performed,

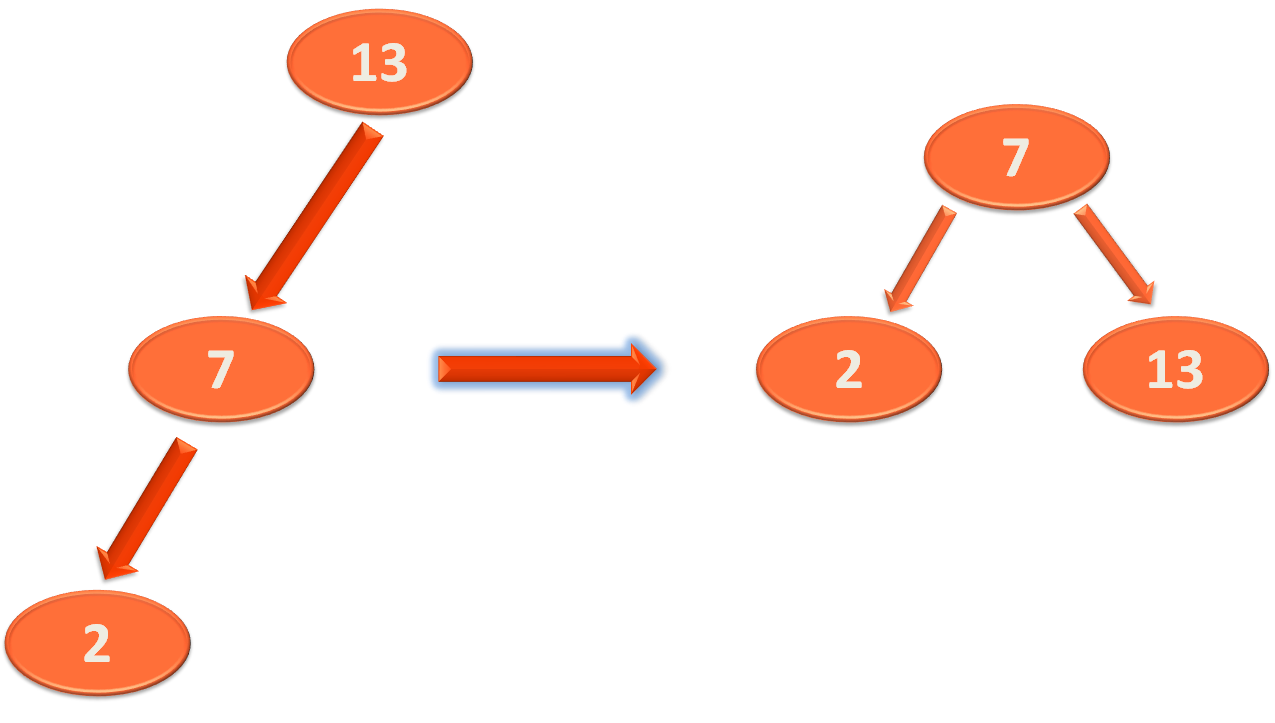
The rest few lines of the method is quite easy to understand.

The height is set by calling the setHeight(...) method.

rootNode.height = setHeight(rootNode)

And finally, the Node newRoot is returned.

return newRoot

And continuing this way we get the below AVL tree.

❮❮ PREV NEXT ❯❯